一道教材课后习题的推广与应用

北京师范大学贵阳附属中学 (550081) 曹 莹 李鸿昌

1 课本习题

2019年人教A版《数学必修第一册》第87页第13题如下:

我们知道,函数y=f(x)的图象关于坐标原点成中心对称图形的充要条件是函数y=f(x)为奇函数,有同学发现可以将其推广为:函数y=f(x)的图像关于点P(a,b)成中心对称图形的充要条件是函数y=f(x+a)-b为奇函数.

(1)求函数f(x)=x3-3x2图象的对称中心;

(2)类比上述推广结论,写出“函数y=f(x)的图象关于y轴成轴对称图形的充要条件是函数y=f(x)为偶函数”的一个推广结论.

2 习题探究

(2)函数y=f(x)的图象关于直线x=a成轴对称图形的充要条件是函数y=f(x+a)为偶函数.

点评：这道课本习题指出了函数的对称性与其奇偶性的关系,通过图象的平移变换是很好理解的.总结可得如下结论:

①函数y=f(x)的图象关于点P(a,b)对称⟺函数y=f(x+a)-b为奇函数⟺f(x+a)-b=

-[f(-x+a)-b]⟺f(x+a)+f(a-x)=2b.

②函数y=f(x)的图象关于直线x=a对称⟺函数y=f(x+a)为偶函数⟺f(a+x)=f(a-x).

3 习题推广

3.1 三次函数图象的对称中心

本习题涉及到三次函数图象的对称中心,经过探究得到如下性质.

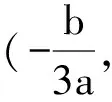
点评：注意到,三次函数f(x)=ax3+bx2+cx+d(a≠0)的拐点(使二阶导数f＂(x)=0的点)正好是它的图象的对称中心.

除了三次函数的图象外,还有哪些函数的图象也具有对称中心呢?经探究,发现某些分式函数、指数型函数和对数型函数的图象也具有对称中心.

3.2 分式函数图象的对称中心

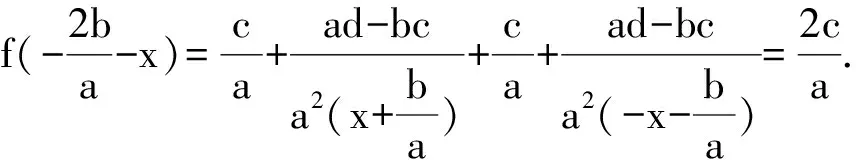
3.3 指数型函数图象的对称中心

证明：因为f(loga|t|+x)+f(loga|t|-x)

例如,函数f(x)=ax-a-x的图象关于坐标原点对称.

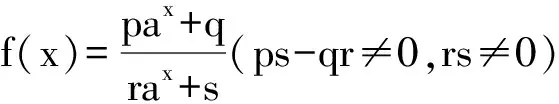
3.4 对数型函数图象的对称中心

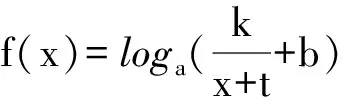
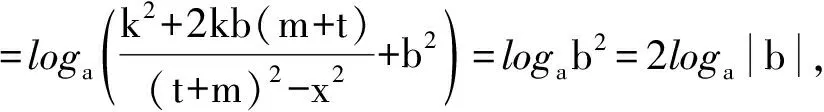
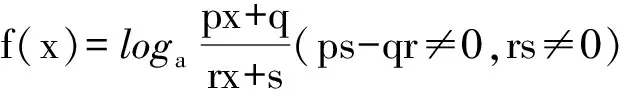
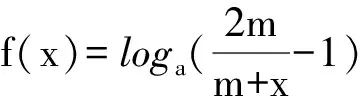
4 应用

f(x)的图象( ).

A.关于点(2,2)对称B.关于点(1,1) 对称

C.关于直线x=1 对称D.关于直线x=2对称

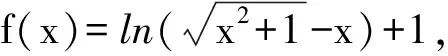
A.0B.6C.12D.24

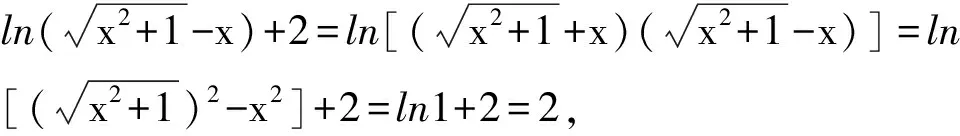
A.f(x)在(2,+∞)上单调递增

B.f(x)在(2,+∞)上单调递减

C.曲线y=f(x)是轴对称图形

D.曲线y=f(x)是中心对称图形

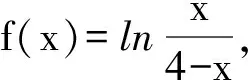
A.y=f(x)的图象关于点(2,0)对称

B.y=f(x)的图象关于直线x=2对称

C.f(x)在(0,4)上单调递减

D.f(x)在(0,2)上单调递减,在(2,4)上单调递增