从通法到“秒杀”,用思维导图解答中考压轴题

陈旭

摘要：利用思维导图可以引导学生通过研究一题多解来沟通各种知识的内在联系，帮助学生将已学的知识形成系统，同时让学生学会从不同的角度，采用合理的观点去思考同一个问题，提高思维的流畅性和变通性，提高解题能力.本文中以一道几何问题的一题多解为例，合理借助思维导图，突破学生思维屏障，拓宽思维广度和深度，提高学生几何解题的有效性.

关键词：思维导图；一题多解；解题能力

1 对一道上海模考试题模型的解法探究

上海市中考数学命题以《上海市中小学数学课程标准》为依据，近几年，试卷的第24题一般都是平面几何和二次函数的综合题，其中几何部分考查相似的情况比较多，而且通常解法不唯一，蕴涵着多种数学思想方法、数学模型，充分体现了课改理念，深入考查学生分析问题的能力［1］.下面笔者以2018年上海市奉贤区一模第24题为例进行说明.

1.1 问题呈现

如图1，在平面直角坐标系xOy中，抛物线y=-x2+bx+c与x轴相交于点A（-1，0）和点B，与y轴相交于点C（0，3），拋物线的顶点为D，连接AC，BC，DB，DC.

（1）求抛物线的解析式及顶点D的坐标；

（2）求证：△ACO∽△DBC；

（3）如果点E在x轴上，且位于点B的右侧，∠BCE=∠ACO，求点E的坐标.

1.2 课堂还原

呈现题目后，让学生思考并展示思路.

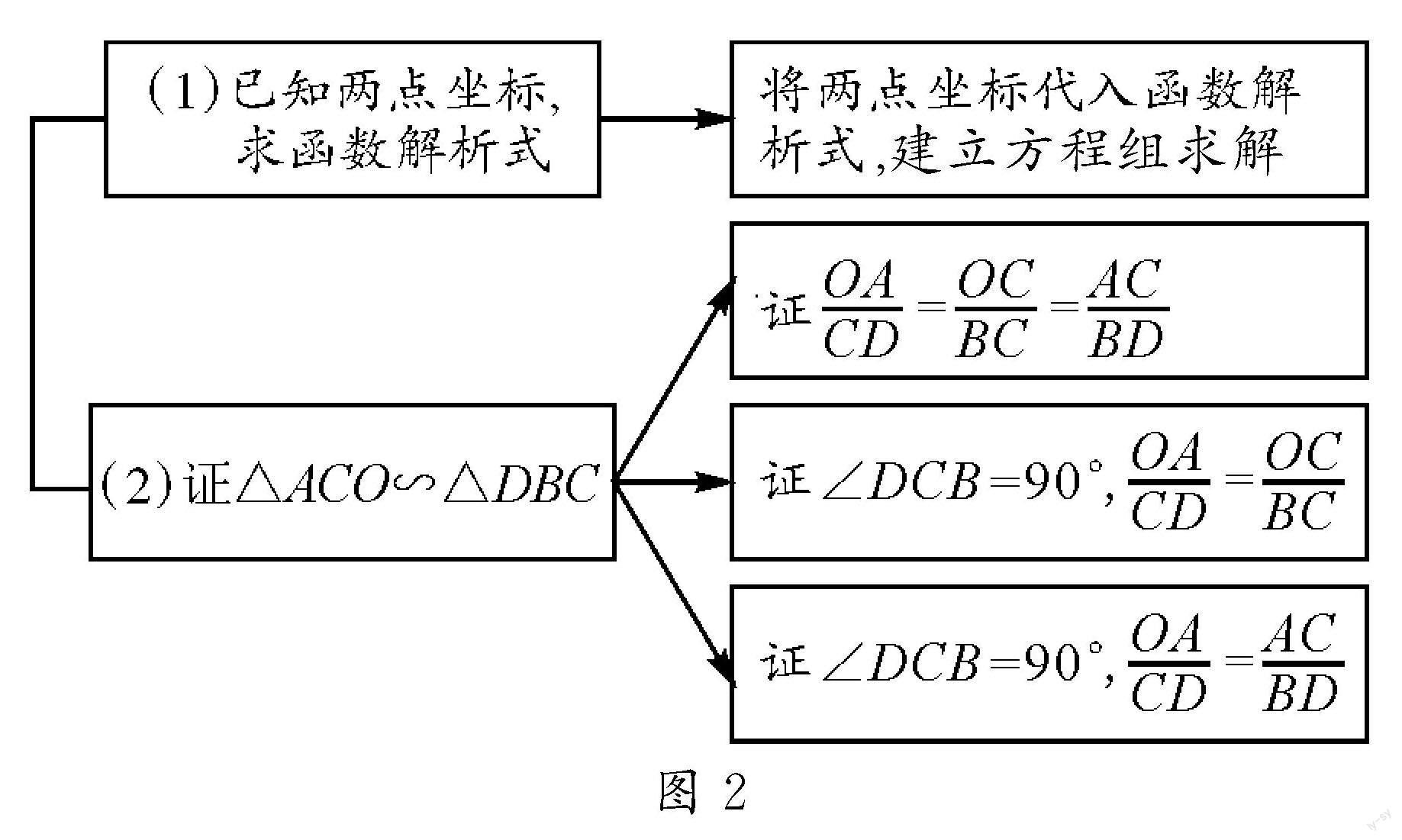
第（1）（2）问对于学生来说比较基础，第（1）问只需利用待定系数法即可求解.作为解决问题的引入，第（2）问提示学生本题重点涉及相似三角形的相关知识，在思维上起到启示的作用.经过讨论，得到前两问的思维导图（如图2所示）.

第（3）问是本题的难点，本文重点研究这一问.一方面，题设条件给出∠BCE=∠ACO，这是角相等的问题，利用该条件如何切入呢？另外一方面，从要求的问题来看，是求点E的坐标，让学生发散思维，又可以从哪些角度入手呢？观察图中的∠ACO，∠BCE，发现它们所在的两个三角形△AOC和△BCE明显不相似，进一步追问该怎么办？学生根据已有的经验，首先会想到构造两个相似三角形，这样就可以和第（2）问联系起来.

经过教师引导和学生讨论后，得出多种处理该问题的思路.第（3）问的思维导图如图3所示.

1.3 解法探究

第（1）（2）问解答如下：

（1）把A（-1，0）和C（0，3）代入y=-x2+bx+c，得-1-b+c=0，c=3，解得b=2，c=3.

所以，抛物线的解析式为y=-x2+2x+3，顶点D的坐标为（1，4）.

（2）令-x2+2x+3=0，则x1=-1，x2=3，所以B（3，0）.利用两点间距离公式，

可得BC=32，CD=2，BD=25，则BC2+CD2=BD2，于是∠BCD=90°，易

证得△ACO∽△DBC（过程略）.

下面重点研究第（3）问，提供如下7种解法.

思路一：从构造相似三角形的方向考虑相似模型，即利用相等角构造相似三角形.

由于∠BCE=∠ACO，△AOC是一个含有∠ACO的直角三角形，因此只需再构造一个含有∠BCE的直角三角形即可.基于这种思路，学生提出以下几种构造方法.

解法1：如图4，过点B作BF⊥CE于点F，易证△AOC∽△BFC，所以AOBF=ACBC，

即1BF=1032，解得BF=355.

设E（m，0），利用两点间距离公式，可得

BE=m-3，CE=m2+9.

由S△BCE=12BE·OC=12BF·CE，可得

3m-3=355[KG-1mm]m2+9.

解得m1=6，m2=32（舍）.

故E（6，0）.

事实上，解法1还利用了几何中经常使用的等面积法，成功地把几何问题转化为代数中的方程问题.此种解法比较常规，属于通法，但是计算稍显繁琐.

解法2：如图5，过点B作BF⊥BC交CE于点F，易证△AOC∽△FBC.过点F作x轴的垂线，垂足为G，可知FG∥OC.由△AOC∽△FBC，

可得OABF=OCBC，

即1BF=332，解得BF=2.

又由OB=OC，即∠CBO=45°，得∠FBG=45°.

因此FG=BG=1.

由FG∥OC，可得FGOC=GEOE，即13=OE-4OE，解得

OE=6.

故E（6，0）.

解法2主要是注意到△COB是等腰直角三角形，进而构造出另外一个等腰直角三角形BGF，然后利用平行线分线段成比例的基本事实，快速得到OE.与解法1相比，计算量大大减少，但是辅助线的添加较为繁琐，也需要学生能够注意到特殊的角度.

在解法2的基础上，有学生提出了解法3.

解法3：如图6，过点E作EF⊥CB，交CB的延长线于点F，易证△AOC∽△EFC.

同解法2，注意到∠1=∠2=45°，可得

△BEF为等腰直角三角形，于是

BE=2EF=2BF.

由△AOC∽△EFC，

可得EFOA=CFOC，即EF1=32+EF3，解得

EF=322.

所以BE=2EF=3.故E（6，0）.

解法3其实也是注意到了特殊的45°角，但是与解法2相比，显然辅助线相对简单，后续的计算过程也比较简便.

同样地，也是注意到了特殊角，有学生提出可以用如下解法来构造相似三角形.

解法4：如图7，过点A作AF⊥BC于点F，可得∠1=∠2=45° .

所以AF=BF=22AB=22，因此CF=2 .

由∠ACO=∠BCE，得∠ACF=∠OCE，

可證△ACF∽△ECO，所以AFOE=CFOC，

即22OE=23，解得OE=6.

故E（6，0）.

以上四种解法的共同点都是构造相似三角形，前三种解法都是构造不同的直角三角形与△AOC相似，解法4是构造直角三角形与△EOC相似.同时，解法1还使用了两点间的距离公式和等面积法，解法2利用了平行线分线段成比例的基本事实，解法3利用了△BEF是等腰直角三角形.相对来说，解法1的辅助线学生比较容易想到；解法4中的△ABC中含有45°角，注意到这一点，就很容易联想到作辅助线AF.解法3和解法4的计算过程相对简单.

完成了上述四种解法后，有学生提出了利用图中∠CBE=135°也可以构造相似三角形，于是得到解法5.

解法5：如图8，在OC上截取OF=OA=1，则CF=2.

连接AF，易得∠AFO=45°，∠AFC=135°，于是AF=2.

易证△CFA∽△CBE，

所以CFCB=AFBE，即232=2BE，

解得BE=3.

故E（6，0）.

上述解法5需要注意到∠CBE=135°，不容易想到辅助线的构造，但是计算过程比较简便.

思路二：构造直角三角形斜边中线模型，即利用相等角（“秒杀”）.

上述五种解法都是构造相似三角形，有没有更加简便快捷的方法呢？跳出构造相似三角形这一框架，要求点E的坐标，在已知点C坐标的情况下，可以通过求出直线CE的解析式，即先求出CE与BD的交点F的坐标来得到.由于△BCD是直角三角形，因此利用第（2）问的结论和第（3）问的题设条件可以推出F为BD的中点，再利用中点坐标公式即可求出点F的坐标.

解法6：如图9，设CE与BD交于点F.由第（2）问结论△ACO∽△DBC，可得∠DCB=∠AOC=90°，∠CBD=∠ACO，

于是∠CBD=∠BCE.

因此CF=BF.

因为∠CBD+∠CDF=90°，∠DCF+∠BCE=90°，

所以∠DCF=∠CDF，即CF=DF，从而DF=BF.

于是F（2，2）.

故直线CF的解析式为 y=-12x+3，则E（6，0）.

思路三：全等模型，即利用相等角，构造全等型（“秒杀”）.

利用隐含条件∠OBC=∠OCB=45°，∠1=∠BCE可进一步推出∠OBD=∠OCE，延长BD交y轴于点F，构造全等三角形，利用全等三角形对应边相等，将求OE的长转化为求OF的长.由于直线BD的解析式非常容易得到，因此易求出点F的坐标，这种解法计算量也很小.

解法7：如图10，延长BD交y轴于点F， 和解法5一样可证∠1=∠BCE.又由∠OBC=∠OCB=45°，可得∠OBF=∠OCE， 从而有△BOF≌△COE，可得OE=OF.由直线BD的解析式为y=-2x+6，可得F（0，6），即OF=6.故OE=6， 即E（6，0）.

解法7中，得到∠OBF=∠OCE后，由于这两个角正好都在直角三角形中，因此也可以使用三角比来得到OE=OF.

解答如下：因为∠OBF=∠OCE，所以tan∠OBF=tan∠OCE，则OFOB=OEOC，即OF3=OE3，因此OF=OE.

上述七种解法的辅助线构造方法不同的一个重要原因是学生处理问题的出发点不同，几种相似模型的辅助线构造方法也不同则是因为构造的相似三角形不同，这是很自然的过程，从本质看，又属于“形变质通、殊途同归”.辅助线通常是解决问题的桥梁，巧妙的辅助线经常可以“柳暗花明又一村”.

2 思考和启迪

列夫托尔斯泰说过：“知识，只有当它是靠积极的思维得来，而不是凭记忆得来的时候，才是真正的知识.”因此，教师在课堂上应把思考的权力还给学生，留给学生充分的思考时间.

对于初中的综合题讲评课，笔者认为在教学时要注重对数学模型的抽象和提炼.“模型”是学生学好数学的一种认知策略.在教学中要充分利用“数学模型”，从不同角度去思考同一道题目的解答方法，让学生大胆地质疑、大胆地思考，从多角度去发现问题.每一个条件不同的延伸方向都是一种不同的解题思路，学生在探究的过程中所获得的会比仅仅接受一种解法更加全面.作为教师，不仅要给学生探究的机会，更要及时收集和分享学生的探究成果.一题多解，沟通了各种知识间的内在联系，有利于形成知识系统，同时让学生学会从不同的角度去思考同一个问题，有利于提高思维的流畅性和变通性，提高解题能力［2］.

参考文献：

［1］中华人民共和国教育部.义务教育数学课程标准（2011年版）[S].北京：北京师范大学出版社，2012.

［2］李士锜，黄兴丰.数学案例教学论[M].合肥：安徽教育出版社，2011.