一道初中几何压轴题的点评

刁琴 石勇国

课题信息：本文系四川省首批一流专业“数学与应用数学专业建设点”（YLZY201902），2022年内江市教育局高校基础教育研究专项课题“HPM視角下城乡初中数学德育的实践研究”的研究成果.石勇国系通讯作者.

摘要：几何问题是中考热点题型的重难点问题，涉及数学知识面宽，变量多，图形复杂.结合2021年孝感孝南区二模初中数学压轴题的点评，给出教学上的几点建议.

关键词：中考数学；三角形相似；动点；动角

从近年全国各省市中考来看，动态几何题已成为中考数学的热点题型之一.这类题按照“观察—抽象—探索—猜测—论证”方式命题，有较好的区分度，具备探究的功能，有力地考查了学生的数学核心素养.然而这类题难度大，知识点跨度宽，多数学生不易掌握.本文中以2021年孝感孝南区二模初中数学压轴题为例，利用归纳、类比、猜想、化归的数学思维，结合数形结合的方法进行求解分析；同时点评了该题的考点、区分度、命题设计，并且给出了变式拓展以及教学上的几点建议.

1 试题求解分析

题目  在△ABC与△CDE中，∠ACB=∠DCE=90°，且∠CAB=∠CDE=θ，点D始终在线段AB上（不与点A，B重合）.

（1）问题发现：如图1，若θ=45°，分别求∠DBE的度数和BEAD的值.

（2）类比探究：如图2，若θ=30°，试求∠DBE的度数和BEAD的值.

（3）拓展应用：在（2）的条件下，M为DE的中点，当AC=23时，BM的最小值为多少？

本题第（1）（2）问是角∠CAD=θ为变化参数，当θ分别取为特殊值时，依次发现△ACD和△BCE全等与相似，求得∠DBE的度数和BEAD的值.

第（3）问是固定角∠CAB，动点是D，抓住∠DBE=90°的条件，利用直角三角形中线定理和θ=30°，则问题转化为求CE的最小值，将动态问题转化为在静态状态下求解.

第（1）问从特殊的值入手，证明三角形全等.根据等腰直角三角形ABC与三角形CDE的边角关系，易证△ACD≌△BCE，进而∠DBE=90°，BEAD=1.

对于第（2）问，利用类比、归纳，发现不变量.根据两角对应相等的两个三角形相似，判定Rt△ABC∽Rt△DEC，有

BCAC=ECCD=13=33.

根据相似三角形的判定定理，即两边对应成比例且夹角相等，确定△ACD∽△BCE.于是

∠CBE=∠CAD=θ，∠DBE=90°，

以及相似比

BEAD=BCAC=33.

猜想：不管角θ多大，均有△ACD∽△BCE，而且∠DBE是直角.

证明方法类似.

第（3）问利用化归的方法，转化最值问题进行求解.根据两个不变量

△ACD∽△BCE，∠DBE=90°，结合

M是DE的中点、直角三角形斜边中线定理和θ=30°，得到

BM=ME=MD=CE.

所以，求BM的最小值，即求CE的最小值.根据直角三角形的斜边大于直角边，可知当CE⊥BE时，CE最小，如图3.

因为AC=23，θ=30°，于是CE=BM=12BC=1.

2 试题点评

2.1 考点知识面宽，区分度明显

试题第（1）问考查了三角形全等的判定.第（2）问考查了类比法、三角形相似的判定、相似比以及归纳法的第一步特殊值验证.第（3）问考查了直角三角形的中线定理、勾股定理、直角三角形斜边大于直角边，以及最值问题.题中附带的两图，包含了等腰直角三角形、特殊直角三角形等9个三角形，3个四边形.涉及2个变量，即1个角度变量∠CAD，1个动点D.考点从等腰直角三角形变化为一般的直角三角形，从角度变化到动点变化，从求比值到求最值.问题由易到难、层次分明，考点之间有机融合，三个小问区分度明显，是一道非常好的几何压轴题.

2.2 考题变中有定，动中有静

该题有两个变量，同时在变化中也有两个不变量：一是△ACD∽△BCE；二是∠DBE是直角.

为了分解题目的难度，将变量θ依次取特殊值进行设问.第（1）问以简单特殊值入门，让考生初步尝试；第（2）问以另外一个特殊值进一步探索，通过类比、归纳、猜想，引导学生发现上述两个不变量.第（3）问将变量θ设置为固定值，以D为动点求最值.通过化归的方法，将动态的问题转化为直角三角形的静态最值问题，最后得到解.

题目设计以学生为中心，让学生从考题中享受探索发现、类比猜想、验证证明的乐趣.选题动静结合，从特殊到一般，在变化之中寻找不变量，在动态之中寻找最小值.三个小问由易到难、逐步深入，相关知识点衔接顺畅，设计精巧，是一道适合探索研究的好题.

2.3 考题变化有度，适合变式训练

本题有两个变量，因此可以设计较多的变式拓展的训练题.例如下面的问题（4）：

（4）若θ=60°，M为DE的中点，当AC=2时，BM的最小值为多少？

另外考虑点D可能在AB的延长线上，可以设计如下问题（5）：

（5）若θ=60°，且D在直线AB上（不与A，B重合），点M为线段DE的中点.若AC=2，当△BMC为直角三角形时，求BE的长.

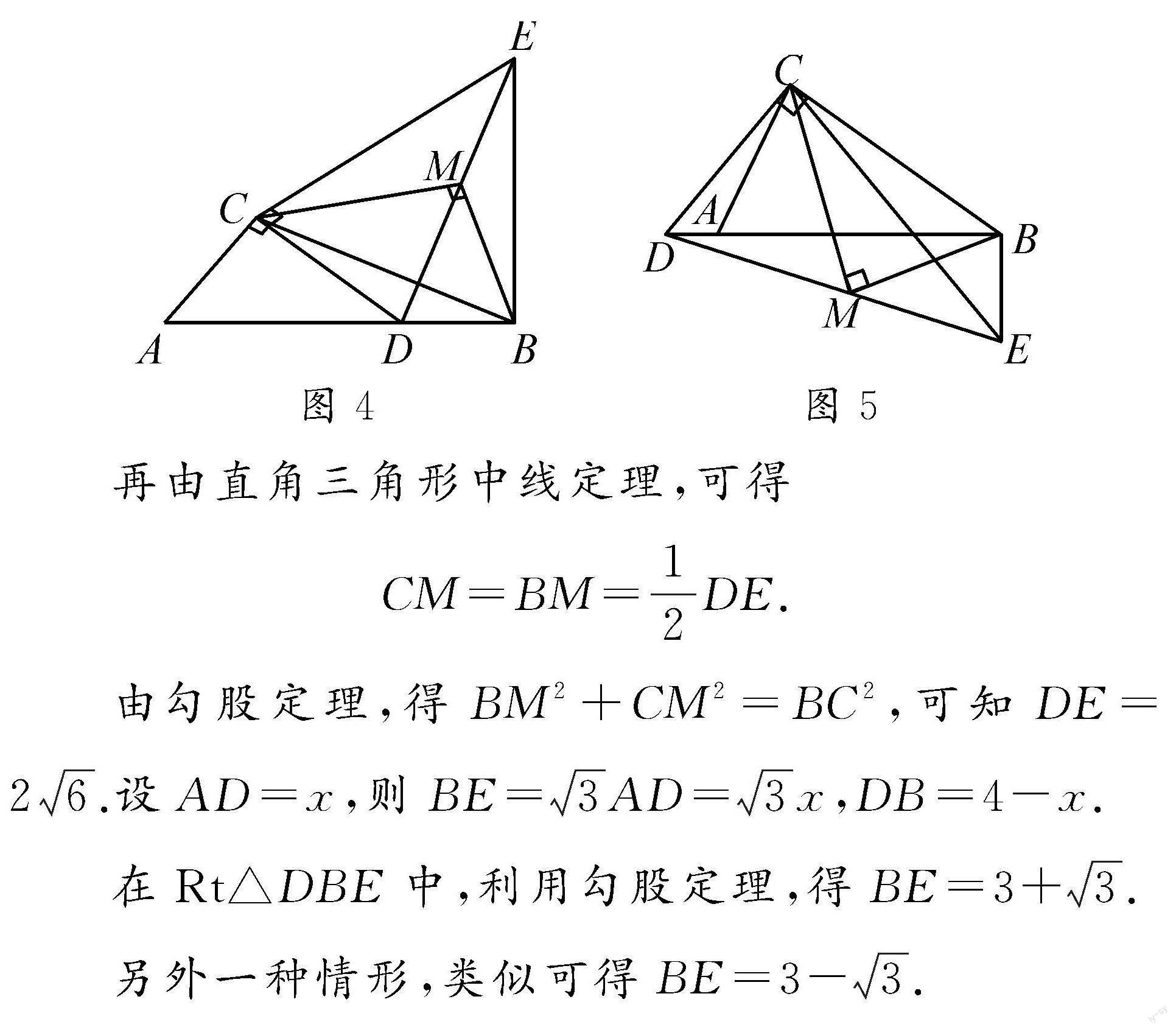
分析：分类讨论，考虑点D在线段AB上和在其延长线上两种情形，如图4，图5.由△ACD∽△BCE，可得

∠ABE=90°，BE=3AD.

再由直角三角形中线定理，可得

CM=BM=12DE.

由勾股定理，得BM2+CM2=BC2，可知DE=26.设AD=x，则

BE=3AD=3x，DB=4-x.

在Rt△DBE中，利用勾股定理，得BE=3+3.

另外一种情形，类似可得BE=3-3.

3 教学建议

（1）培养学生逻辑思维与直观想象能力

针对几何题，引导学生读题并且联想变化过程、绘制多幅图展示动态过程，从题目中提取关键信息，在众多的三角形中找出全等或相似三角形，利用相似比，根据三角形重要定理，列出边角所具有的关系.利用数形结合的方式，对题目进行双重表述，锻炼逻辑思维与直观想象能力.

（2）培养学生数学思维方式

按照数学的思维方式传授数学知识，提升学生的四种数学思维：从特殊到一般的归纳思维、触类旁通的类比思维、化繁为简的化归思维、“反其道而思之”的逆向思维.引导学生学会遇到问题时该如何发现规律、举一反三、变换化简、反向思考，逐步养成数学思维方法，能够用数学的眼光看问题，了解问题的本质，分析出难点，选择合适的数学方法，用数学语言表达求解过程，以此训练学生的思维方式，提升数学核心素养.

（3）教学融入德育实践

对复杂的动点几何题分析不难发现，变量在变化过程中常常会出现数量关系保持不变的情形.这就需要我们勇于探索，排除动态变化的干扰，用数学的眼光去发现不变的规律，大胆猜测，小心求证.教学中要融入德育实践，在润物细无声中，培养了学生讲理、严谨的理性精神，鼓励学生认识与评价数学，养成正确的理想信念，增强学生的兴趣与自信心，培养坚韧不拔、谦虚谨慎与志存高远的品质，以及追求创新的精神.