数学高阶思维的生本课堂演进

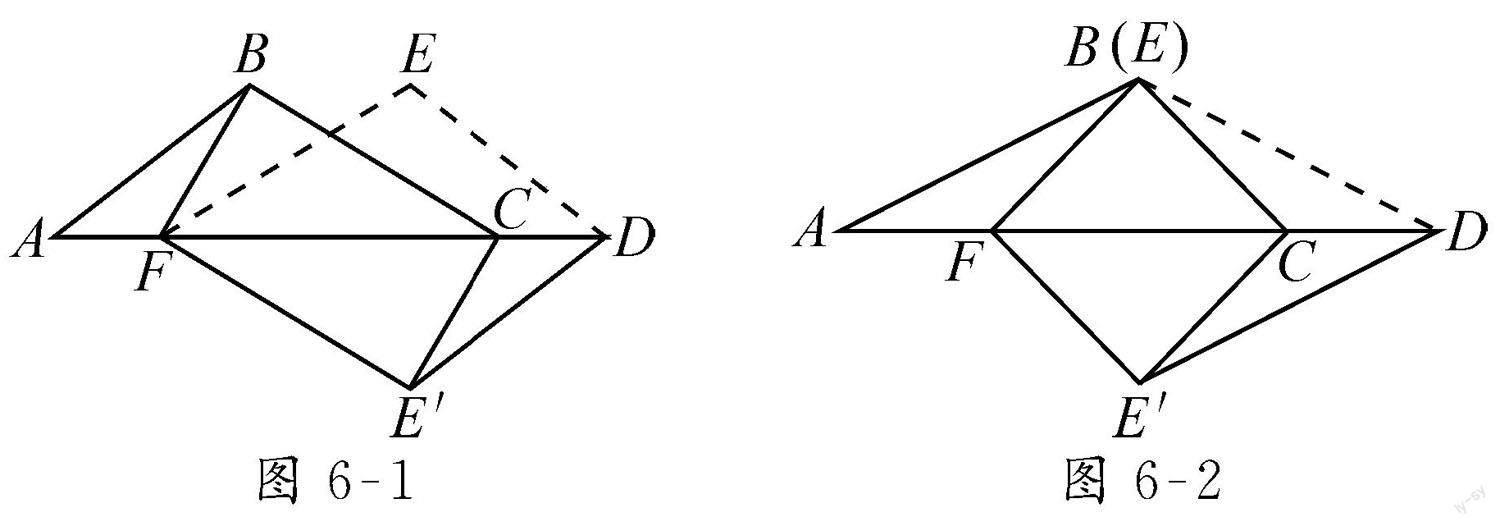
摘要：课堂是由学生生成数学任务、生长数学知识，开展交互式数学活动，梳理自己的思维，评价和反馈其他同学的思维，经历思维的打磨过程.课堂中的练习题是由学生根据习得的数学知识自己编制而成的数学题目.经过“独立编题；小组内交流、反馈；组际交流，将各组编题进行归类和排序；问题解决，追踪思维，提炼方法；展示编题路径、提炼编题的方法”等环节，充分体现学生主体性和思维的交互、评估和创造.

关键词：数学高阶思维；生本课堂；课堂演进

培养学生数学高阶思维的重点是课堂中使学生深度卷入数学活动过程，实现思维进阶.课堂中践行“不用PPT，不用现成的数学题”［1］，由学生生成数学任务、生长数学知识，亲历数学知识的发生、发展过程.课堂中的练习题由学生根据习得的数学知识自己编制而成，让学生亲历提出问题、分析问题与解决问题的过程.课堂以学生主动参与为本，以深度经历和体验为径，以思维层次的提升为旨.下面以“特殊平行四边形”［2］单元复习课为例，谈谈“生本、生成、生长”的课堂演进过程.

1 由学生梳理知识，架构体系

问题1  你有哪些办法判定一个四边形是平行四边形？

学生回顾之前学过的知识，通过思考，回答平行四边形的判定方法，教材提供了三个判定定理.

问题2  能否说出所有判定平行四边形的方法？

这个问题其实就是指向于学生去寻找判定方法的规律或者基本特征，追踪“判定”的基本方法.

学生面临任务时，会产生思维的冲突.首先激发独立思考，产生想法，需要得到其他同学共鸣；碰到困惑和挫折，需要得到其他同学提示和启发.这样学生就会产生交流需求，自觉进入群组互动环节.

群组互动：让组内每位学生“出声思考”——“说出”自己的思维及其发现过程，实现思维曝光.

小组反馈：要判定一个四边形是平行四边形需要两个特征条件，可以考虑边的特征，也可以考虑角或者对角线的特征，梳理得到平行四边形有十个表现特征，分别为两组对边相等、两组对边平行，两组对角相等，两组邻角互补，两条对角线互相平分.这十个特征里任选两个作为条件就可以得到四十五种判定平行四边形的方法，如表1.至于这些判断方法是否正确，有待验证.如果是真命题，则需要证明；如果是假命题，则需要举出反例.

问题3  可以用这种方式类比探究其他图形吗？

学生自主探究：独立思考—群组互动—反馈.要判定四边形是矩形，还需增加一个矩形的特征.矩形有两个表现特征，选其中一个，即可在原来判定平行四边形的基础上判定矩形.同样的道理要判定四边形是菱形，还需增加一个菱形的特征，菱形有三个表现特征，选其中一个，即可在原来判定平行四边形的基础上判定菱形.同学们得到45×2×3=270种判定一个四边形是正方形的方法.因而非常激动，由同学归纳判断一个四边形是平行四边形的基本策略，如图1所示：

这其实是方法的习得，不仅可以重新梳理整合之前学习过的图形的判定方法，还可以用这样的方法探究新的图形.

2 由学生编题，将知识转化为问题解决

任务：既然学习了判定一个四边形是平行四边形方法，那么用这些知识可以解决什么样的问题呢？

此问题引起学生思考如何将知识转化为数学题，养成数学知识的应用意识.

环节1：每个学生独立编题.

环节2：学生编题后小组交流，保证编的题更有科学性和针对性.

通过互动，学生的思维能得到回应和反馈.吸收各小组反馈的不同结论、不同思考路径和创造性的想法，并对自己的思维进行进一步加工，因此，群組交流的过程是思维的优化过程.

环节3：每一组反馈所编的不同类型的题.

环节4：组际交流.

将各组反馈的所编题目按不同类型、不同难度进行归类和排序，使解决问题变得有序而有梯度.

环节5：呈现最终分类、分层的学生编题.本节课组际评估出的思维水平层次较高的两道编题如下：

例1  如图2，在△ABC中，AB=AC，AD⊥BC，垂足为D，AN是△ABC外角∠CAM的平分线，CE⊥AN，垂足为E.

（1）求证：四边形ADCE为矩形；

（2）添加什么条件时，四边形ADCE是一个正方形？

例2  已知，两个含30°角的三角板ABC和FED如图3-1放置，现翻折三角板FED到FE′D，如图3-2）所示.

（1）求证：四边形BFE′C是平行四边形.

（2）要使四边形BFE′C是矩形，还需要什么条件？有没有办法使它为正方形？

3 由学生追踪解题和编题过程，提炼方法

环节6：解决问题，质疑、拓展.

（1）要求所有学生将他组编的题，落到笔头.

（2）反馈不同解法、思路及其发现的路径；反馈遇到的挫折及其解决办法；反馈存在的疑问或质疑；反馈有创造性的想法，包括有创造性但没有形成结论的想法、有创造性但结论错误的想法；反馈可能碰到的典型错误.

（3）由学生对编题和解法提出质疑和变式.

（4）教师隆重地板书，记录学生的表达.

各组在互相点评、反馈的过程中，吸收并优化了自己的思维．

环节7：展示编题路径、提炼编题方法.以供没有编出题目或者不是按这样的思路编题的同学学习、反思和评估.

编得例1的同学反馈：要编一个矩形判断的问题，可由平行四边形加一个直角的条件得到，而平行四边形可以由两组对边分别平行得到.其中一组对边平行由“角平分线+等腰三角形”得到;另一组对边平行和直角，由“垂直于平行线的两直线”得到，如图4所示.

编得例2的同学反馈：如图5所示的流程，我们组想要用一种对边平行且相等来得到一个四边形是平行四边形，而对边相等可以由全等得到，我们每个人手头上都有两副三角板（用同是含30°角的直角三角板），如图3-1，两条斜边一部分重叠在一条直线上，就满足了第一个条件.然后，想要用内错角相等来得到对边平行，这里有内错角，但是没能得到平行线的内错角，于是把一个三角板翻折下去，如图3-2，只要判断四边形BFE′C是平行四边形即可.

评析：这个环节最有创造性的表现是将三角板实物操作过程“翻译”成数学图形，补全△DE′F，尤其补全在实物操作中并不存在的两条线段BF和E′C是题目编成和实际问题数学化的关键所在，“画出图形”需要学生正真理解问题的本质.

接着，按照图形特征研究的一般方法，想到在平行四边形的基础上，需要添加什么条件得到一个矩形呢？我们在平行四边形BFE′C的∠FBC处添加了一个直角符号，但图中∠FBC明显不是一个直角，所以不能直接画一个直角符号就表示它是直角了.先把平行四边形画成矩形，判断它还需要补充什么条件.

评析：从图3-2到图6-1，对学生来说是一个非常简单的尝试，但对下一步起到了重大的作用.因为紧接着他们要补充条件得到一个正方形.

根据刚才的思路，先把这个正方形画出来，满足正方形的特征，正方形的对角线平分一组对角（还需满足FB与FE′对称），而根据操作，FE′是由FE翻折得到的，因此，当平行四边形BFE′C是正方形时，FB与FE重合，所以点B与E重合，得到图6-2.

从图6-1到图6-2，是学生创造性思维的体现，它来自于数学知识和数学学习本身的逻辑.最后创造性得到综合问题：△ABC沿AC的一条垂线对称得到△DEF（如图3-1），再沿AD所在直线对称到△DE′F（如图3-2）.（1）求证：四边形BFE′C为平行四边形.（2）再添一个什么条件可得到矩形、正方形呢？学生经过作图得到图6-2，从而确定题目条件．

学生编的题完全达到了本堂课所要求的思维水平层次，给学生带来了很大的鼓舞、震撼和触动.

组际提出质疑：三角板按图3-1放置，本身是一个对称图形，平移就可以直接得到平行四边形，那么他们组通过翻折得到图3-2，想得到平行四边形考虑再对称，两次轴对称就成了一次中心对称，直接得到平行四边形.

评析：整个构图过程中，学生自己尝试条件的构造，经历了由知识点到图形符号到数学问题的构造过程，学生的评价和质疑促进学生从不同角度进行思考，对问题的本质有了更深层次的理解.

环节8：评价解题和编题.（1）自我评估.有什么思维的增长？有什么方法、能力的提升？（2）群組学生评价和质疑.小组以题目原创、新颖、思维含量高、解法多样、编题方法可操作等为评价标准.（3）教师评价.以学生为主体的课堂中，学生思维的深度在于群组互动时，教师能否敏锐地抓取到学生生成的创造性信息及不同的思维路径.教师要大张旗鼓地鼓励学生表达群组互动中产生的质疑、有创造性的想法.这是对学生创造性思维的一种肯定，倡导学生不只是追求正确的结论，更多地去追求创造性思维过程.

评析：由学生编题，使问题产生（编题及方法）与问题解决（解题及方法）形成闭环，小组交流、反馈，促成学生创造性思维，提炼编题的方法.教师的行为、煽动性的追问，是鼓励和回应学生的创造性思维和方法的重要策略.

4 生本课堂发展学生高阶思维的关键

促动学生高阶思维的课堂，关键在于能否以学生为主体.这需要解决以下三个问题：

（1）学生编出来的问题不是教师想要的问题怎么办？学生之所以编出这些问题，是他认知范围内知识产生的路径所理解的问题表述.不用PPT的好处就是可以把这些问题纳入课堂要解决的问题，如果预设PPT的话，那么学生编出来的问题不在PPT预设之内，就会经常出现这样的状况：你这个问题很好，我们课后去研究.因此，利用PPT会造成教学没有办法以学生为中心.至于这个问题的科学性和内容的针对性在小组互动的时候，已经筛选过了，并进行了分类、分层.因此，凡是学生编出来的问题都是课堂中要解决的问题，学生编出的问题反应了学生的疑问和当前的认知水平，这些题可能教师自己没有想到，因而把学生的问题纳入到课堂中来，同时，教师的教学策略也应据此作出改变.

（2）课程内容所涉及到的数学知识，如果学生编写的问题中没有得到反映和完善怎么办呢？事实上，促动学生有序思考，类比已有知识探究的方法，课堂上所要研究的问题基本上学生都会涉及到；如果没有想到，小组同学互动一下，经过思维的碰撞就会得到这些问题；进一步教师在巡视时可以介入到小组中对类似的探究进行追问，必然会追踪到问题的本源.

（3）学生为主体的开放课堂怎样收回来呢？实际上每次上课都要做好整个内容的设计以及PPT（包括PPT的每一张动画），然后，上课之前经过深思熟虑会把PPT删去，之所以能够把课堂收回来，最主要的原因是教师对课堂内容非常娴熟.教师课堂上要关注教学内容和学生的反应，在数学内容非常熟练的情况下，教师的注意力可都放在学生身上.学生编出来的问题，如果正好是预设体系里有的内容，便可以直接把这个问题纳入到本节教学体系中；如果原预设中没有，那就是学生现场生成的创造性产物.教师要对学生新生成的问题作出判断和评估，也就是说，能不能挖取到学生原创的东西，是对教师最基本能力的考量.

参考文献：

[1]张娟萍.高阶思维：初中数学教学变革的新视角[M].杭州：浙江大学出版社，2017：172-176.

[2]张娟萍.发展高阶能力—提升数学思维层级的教学指南[M].杭州：浙江大学出版社，2020：62.