数学教学中学生思维的启发与培养

周勇军 肖乐斌

摘要：米·伊·加里宁对中学生们说过“数学，可以让大脑更有条理，并且培养思维的逻辑性”，这是对思维在数学中的地位与作用的高度概括.中学数学教学中在培养学生思维能力上应如何有所突破和提高？数学知识的获取应是思维的结果，导出这些结果的思维过程，是培养逻辑思维的最佳时机和重要途径.要想在教学过程中培养学生的思维能力就需要让学生亲自参与感知、分析、综合，抽象、概括的过程，如果忽视学生的认识和思维过程，就会削弱思维能力的培养.本文中针对如何在获取知识的过程中培养学生的思维能力提出几点教学建议.

关键词：思维；基本语言法；基本图形法

1 教学中要注意知识的迁移

“以其所知，喻其不知，使其知之.”这句话说明了用已知去获取新知的道理，后续知识既是新知识，又是已学知识的发展.数学教材通常在较多的例题前设计“准备题”与“复习题”，其目的也就是沟通新旧知识，让学生联系旧知识，学习新知识.因此，在教学新知识时，应充分利用教材知识的内在联系，为学生指引一条由已知探求未知的道路，从而发展学生的逻辑思维能力.

例1  比较下列两个数的大小.

（1）-1.9，-2.1；  （2）-58，-98.

其实，比较1.9与2.1，58与98的大小，属于小学数学内容.

在学习新知识时，先复习旧知识，弄清两个正数的大小，再加上一个符号法则，新问题就迎刃而解了.这样，立足于迁移，通过复习题，步步引导，促使学生了解新旧知识的联系和变化，并正确表述自己的思维活动过程，由此提高学生的抽象概括能力，进而促进逻辑思维能力的发展.

2 代数课上用基本语言法引导学生思维

基本语言法是指将复杂的代数问题逐步转化为简单的、学生能求解的形式.它是代数课上启发学生思维的重要方法之一.下面结合例题具体谈谈这种方法在启导学生思维方面的具体运用.

例2  “x的3倍与y的差除以x与y的2倍的和的商”，如何列代数式.

运用基本语言法启导学生思维，首先引导学生观察题目结构.（用提问的方式启发学生思维.）

问题  同学们，你能说出这段文字表述中含有几种运算吗？（让学生在思维活动前，对问题内容有初步的认识.）

学生都能很快回答有“差、和、商”.同时，提醒学生在这些关键字眼上作上记号.

接着进一步提问：谁能用最基本、最简洁的语言说出这句话的大概意思呢？（让学生在不自觉中运用基本语言法来找到思维的突破口.）

学生可能有两种典型的回答：

（1）差除以x再加上y的2倍的和；

（2）差除以和的商.

通过引导学生分析，原题目要求的问题可最终落脚到一个“商”字上.进一步让学生分析“到底是什么与什么的商呢？”学生很快会得出是“差与和的商”.其中，（1）的错误在于没有把握住基本语言的核心“商”.

最后，向学生明确指出：实际上，大家刚才使用了一种将复杂的代数语言转化为基本语言的方法，我们把这种方法称为基本语言法.从上面的分析可以看出，基本语言法能让我们迅速、准确地捕捉到问题的主要矛盾.只要抓住了主要矛盾，学生的思维活动就会自然而然地正常、活跃、有序的运转.为了解决主要矛盾，学生思维的能动性就会自动地推动其思维活动去处理最需要解决的次要矛盾.对于例2，学生为了能解决“差除以和的商”就会自然地去求“谁的差”“谁的和”.

基本语言法是一种启导与培养学生思维行之有效的方法.它以辩证唯物论中的矛盾论为理论依据.要掌握好这种方法，需要学生有较强的语言驾驭能力，能抓住问题的主要矛盾准确进行转化.

为了能使学生对基本语言法有更清晰的认识，下面再给出一道文字语言少而数学语言多的题目.

例3  设y=a（x2+2x+4）2+3a（x2+2x+4）+b的最小值是37，且x=-2时，y=57，求a，b的值.

对于此例，如何具体地引导学生运用基本语言法去分析、转化这里不再赘述，这里仅将使用基本语言法的转化过程整理如下.

通过思维，一般学生根据条件能够将x＝-2，y=57代入原函数式化简，整理得到28a+b=57.

原题可简化为：

设y=a（x2+2x十4）2+3a（x2+2x+4）+b的最小值是37，且28a+b=57求a，b的值.

引导学生观察函数式，为了简化，设u=x2+2x+4，则u＝（x十1）2十3≥3.

进一步可简化为：设y=au2+3au十b（u≥3）的最小值是37，且28a+b=57，求a，b的值.

将u=3代入y=au2十3au+b，得18a+b=37.

原题最后简化为：

设18a+b=37，且28a+b=57，求a，b的值.

3 几何课上用基本图形法引导学生思维

基本图形法是运用基本图形探索几何解题思路的一种方法.它有助于提高学生的几何解题能力.

它的模式是：将问题分解或构造出若干个起主要作用的基本圖形，推出明显（或隐藏）的性质，根据结论选择组合，通过推理证明解决问题.

下面结合例子进行分析.

例4  如图1，ABCD中，AE平分∠BAD，BM平分∠ABC，CM平分∠BCD，DE平分∠ADC.

求证：四边形MNEF是矩形.

引导学生审题，首先对题目的已知条件及整个图形有一个大致的认识.这是运用基本图形法的基础.

问题1  要证四边形MNEF是矩形，只需证什么就行了？

学生的回答可能有多种，但都离不开证“四个角都是直角”.（这是启动学生思维的开端.）

追问：四边形MNEF的四个角是怎样形成的？（这是引入基本图形的关键，也是学生思维能否连续的关键点.）

学生一般都能回答：每个角都是由一对角平分线相交形成的，并且是由一组平行线的同旁内角形成的.

问题2  一组平行线的同旁内角的平分线相交形成的角有什么特点呢？

这就自然将问题转变到对基本图形的探索上了：

（1）如图2，已知AD∥BC，AN平分∠BAD，BN平分∠ABC.求证：AN⊥BN.

（2）如图3，已知AB∥CD，BM平分∠ABC，CM平分∠BCD.求证：BM⊥CM.

为了能使学生对基本图形法有更清楚的认识，下面再举一个较复杂的例子.

例5  如图4，ABCD为圆内接四边形，AC和BD交于点M，AE⊥BD于点E，BF⊥AC于点F.

求证：EF∥CD.

此题线条比较多，图形较复杂，如何运用基本图形法来启导学生思维呢？其运用过程简述如下：

第一步，要求学生在图中寻找所要证的基本图形是什么.学生不难找出所证图形为图5.

结合此基本图特点，让学生自己得出：要证EF∥CD，即证∠CDM=∠FEM.

第二步，根据第一步的结论，学生的思维就会转向在原图中寻找∠CDM与∠FEM.教师这时可以和学生共同分析，得出：

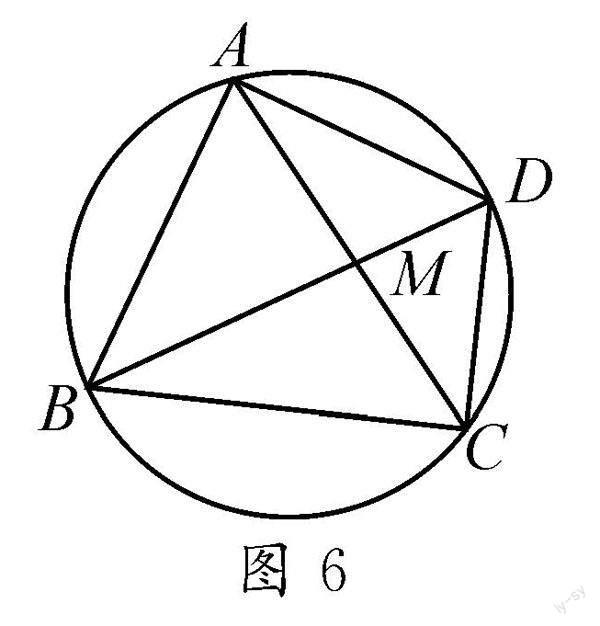
（1）∠CDM位于原图的基本图形是外围图形，如图6.

隐含结论：∠CDM=∠BAM.要证∠CDM=∠FEM，即只需证∠FEM=∠BAM.

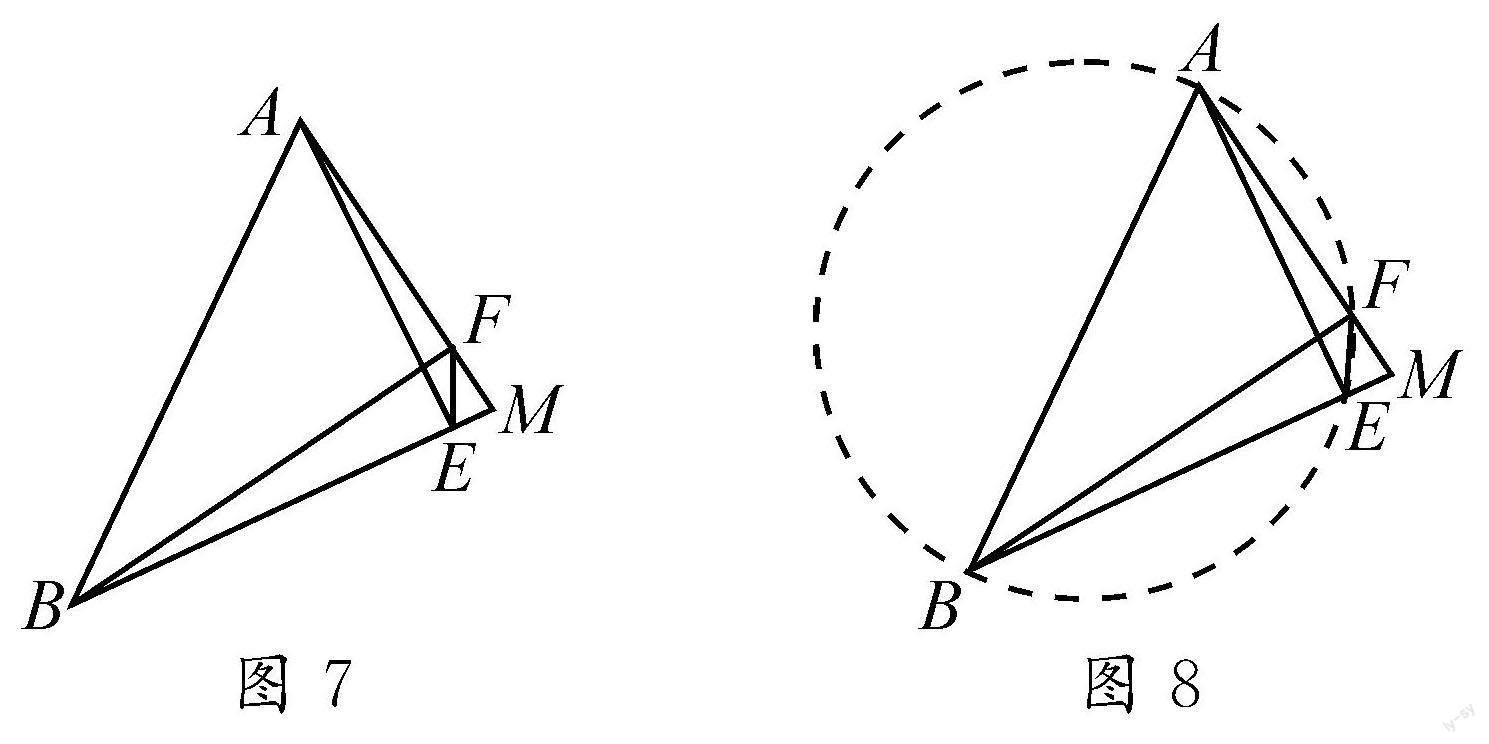
（2）∠FEM位于原图的基本图形是核心图形，如图7或图8.

引导学生观察，就会发现核心图形中的隐含性质——Rt△ABF与△ABE共圆，深化核心图形.

联系第一步，最后确定要证∠FEM=∠BAM，这两个角都在核心图形中.学生此时的注意力就可全集中于该图中，不难证明∠BAM=∠FEM.

第三步，学生根据结论，选择组合完成整个几何问题的证明.

从以上例子可以看出，基本圖形法运用得当，确实能使学生主动参与活动，准确有序地完成几何问题的证明.

在数学教学中，注意新旧知识之间的联系与迁移、基本数学语言中的核心字眼，融合基本图形的应用与分解组合，对培养和启发学生的思维有重要的作用.