可降阶的高阶微分方程中的一个教学案例

刘海涛 钟文敏 李响军

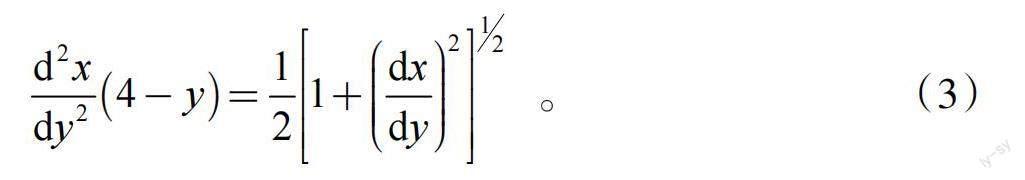
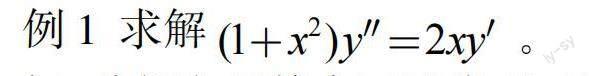
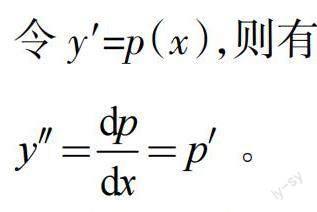
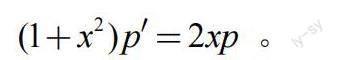
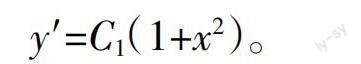
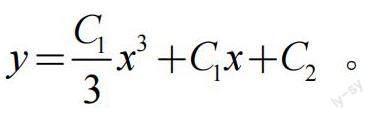
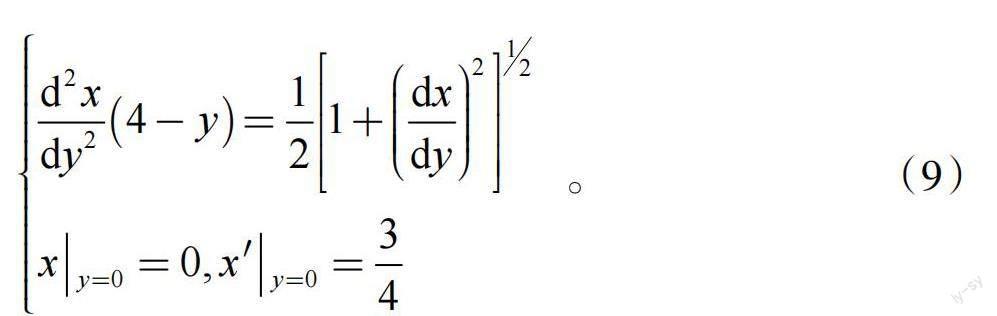
摘  要：针对本科高等数学课程中可降阶微分方程教学内容的特点以及军队院校育人要求，为了更好地提高学生学习积极性、培养学生数学应用能力，以导弹飞行轨迹问题为切入点设计教学案例，通过创设情景、提出问题，引导讨论、建立模型，归纳分析、引出教学内容，分析讨论、讲解求解方法，回归问题、培养应用能力等五个环节，对教学过程进行重新设计，方便教师使用。

关键词：教学案例；可降阶的高阶微分方程；高等数学；数学应用能力；教学设计

中图分类号：G642      文献标志码：A         文章编号：2096-000X（2023）32-0099-04

Abstract： In view of the characteristics of reducible higher order differential equations in Higher Mathematics of the undergraduate course， and the education requirement of military academies， in order to improve students' enthusiasm for learning and cultivate their mathematical application ability， the teaching case is designed with the missile flight trajectory as the starting point. Through creating scenarios and raising questions， guiding discussion and giving cases， summing up and leading to the teaching content， analyzing， discussing and explaining the method， returning to the problem and cultivating application ability， the teaching process has been redesigned for the convenience of teachers.

Keywords： teaching case; reducible higher order differential equations; Higher Mathematics; mathematics application ability; teaching design

基金项目：军队院校教学成果立项培育项目“为战育人导向下的《工程数学》课程教学改革实践”（NUE2022TA01）

第一作者简介：刘海涛（1982-），男，汉族，河北廊坊人，博士，副教授。研究方向为应用数学。

微分方程是高等数学中一个重要教学内容，在同济大学第七版《高等数学》教材中出现在第七章，对于培养学生抽象思维和分析解决实际问题的能力有重要作用[1]。通常，大学一年级学生往往求知欲旺盛，在学习过程中希望学以致用。特别是对军队院校大学一年级学员而言，浓厚的军营氛围以及未来的岗位特点使他们更希望将所学知识与军事问题联系起来。为了调动学员的学习积极性，培养学员数学应用能力，本文设计了一个有军事背景的以导弹飞行轨迹问题为切入点的教学案例，旨在激发学生的学习兴趣，引导其将理论与实践联系起来，提高创新意识和创造能力[2-3]。

在此部分教学内容之前，学生已经学习了一元微积分学，以及几种典型的一阶微分方程及其解法，从而对于微分方程形成了一些基本的认识。而本节内容即可降阶的高阶微分方程则是微分方程教学内容的又一个重要组成部分，主要体现在：首先，本节教学内容是学生第一次接触高阶微分方程，是他们学习更多不同类型微分方程的过渡和橋梁；其次，本次教学内容中的“降阶法”，是求解许多高阶微分方程的一种基本思路，对于后续课程的学习乃至一些实际问题的解决都有重要作用。

传统教学方法通常是以分析可降阶微分方程的特点为思路引出这部分教学内容，这对于学生掌握好这部分理论知识固然重要，但纯粹从数学知识体系角度设计的教学过程难免显得枯燥，不容易引起学生的学习兴趣。探究式教学和案例式教学以具体问题为引入，对于调动学生的学习积极性有很好的作用，同时通过创设有军事背景的问题情境，并以问题为牵引的方式开展教学，有助于更好地调动学生的学习状态，培养学生的分析问题、解决问题的能力[4-5]。基于此，本文通过抽象和简化，给出一个基于导弹飞行轨迹问题的教学案例，方便教师在教学过程中使用。

一  教学目标

通过本次课的课堂教学，使学生达到以下目标：一是会辨识常见的可以用降阶法求解的微分方程；二是掌握可降阶微分方程的求解方法，领会“降阶法”的基本思想；三是通过利用所学知识解决导弹飞行轨迹问题，提高分析问题、解决问题的能力。

二  教学设计

本案例主要讨论一种可以用降阶法求解的高阶微分方程。首先通过一个学员较感兴趣的军事问题引入；然后，分析该问题的特点，并引出教学内容；接着，研究讨论解决该问题的方法；最后解决开头提出的军事问题。

根据上述分析，将教学流程设计为以下五个环节。

第一，创设情境，提出问题。通过一个学生较感兴趣的军事问题，适当配以视频、文字等素材创设情境并提出问题，即如何确定导弹在跟踪和命中空中目标过程中的飞行轨迹。

第二，引导讨论，建立模型。对问题进行适当抽象和简化，通过建立该问题的数学模型，得到描述该问题的微分方程。

第三，归纳分析，引出教学内容。通过分析归纳该方程的特点，引出教学内容，即可降阶的高阶微分方程。

第四，分析讨论，讲解求解方法。通过分析微分方程的特点，提炼出用降阶法求解微分方程的一般过程，并结合例题加以巩固。

第五，回归问题，培养应用能力。利用所学方法解决开头提出的导弹飞行轨迹确定问题，激发学习兴趣，提高学生的数学应用能力。

三  教学流程

（一）  创设情境，提出问题

针对军校学员的专业背景特点，建议选取已公开的导弹射击演练视频作为课程的起始，以此创设教学情境，使学员迅速进入良好的学习状态。通常，导弹跟踪和命中空中目标的过程可以分为三个阶段：一是侦察预警系统将目标运动轨迹、飞行速度等实时参数通过信息系统同步发送到导弹发射平台；二是导弹发射平台自动计算射击诸元，完成射击准备；三是发射导弹，跟踪并命中空中目标。

由于整个过程是一个十分复杂的系统工程，因此，需要引导学员关注与本次课程内容紧密相关的部分，即在第二阶段导弹发射平台在进行射击准备的过程中，如何确定导弹的飞行轨迹？

至此，创设情境环节结束，整个过程持续约2～3分钟，并由此转入下一阶段，即引导学员参与讨论，进而建立该问题的数学模型。

（二）  引导讨论，建立模型

一般而言，由于实际问题往往较为复杂，因此为了用数学方法加以解决，常常需要通过抽象和简化，建立其数学模型。从另一个角度看，正是由于高等数学教学内容非常抽象，因此只有建立了实际问题的数学模型，才能更好地将其与所学知识紧密关联起来。

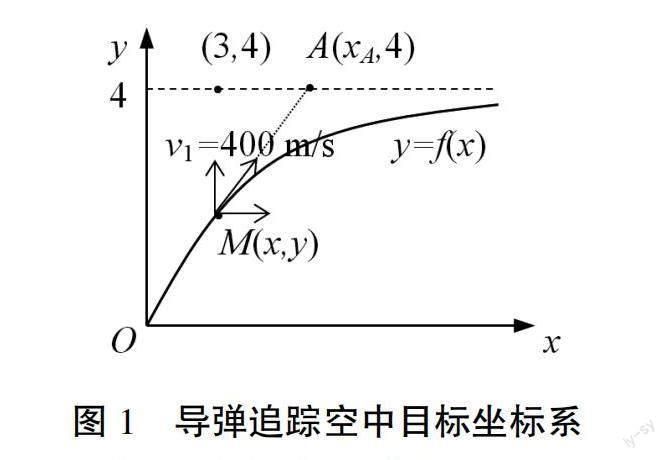
针对导弹飞行轨迹确定问题，首先需要建立描述该问题的直角坐标系。假设在发射时刻t=0时，导弹位于坐标原点，不妨假设空中目标位于点（3，4），并且以200 m/s的速度沿x轴正向飞行。

接着，不妨假设导弹飞行速度为400 m/s，并且导弹采取的导引律为“尾追法”，即其在飞行过程中始终指向空中目标。为了求出导弹的飞行轨迹，记其飞行轨迹为函数y=f（x）。显然，飞行轨迹函数中的x，y都是时刻t的函数，因此要求出该函数，就需要分析x，y随时间的t的变化规律。

记导弹在t时刻位于点M（x，y），根据已知条件，导弹在飞行过程中始终指向空中目标，因此导弹的速度方向始终与导弹当前位置M点与目标t时刻位置A点的连线一致。

设空中目标在t时刻的位置坐标是（xA，4）。则由于目标的初始位置是点（3，4），而飞行速度是200 m/s，因此容易得到A点的横坐标为xA=3+200 t。

又因为导弹始终指向目标，因此点M处的切线斜率等于M点和A点连线的斜率，即

再把导弹的速度进行分解，两个沿坐标轴的分速度的平方和即为导弹速度的平方，由此得到

利用所得到的式（1）和式（2），通过整理消掉变量t，就可以得到导弹运动轨迹满足的微分方程为

求解出这个微分方程，就可以确定导弹飞行轨迹。也就是说导弹飞行轨迹的确定问题转化為了高阶微分方程的求解问题。

该过程大约持续4～5分钟。由此转入下一环节，即通过归纳和分析，引出本次课的教学内容。

（三）  归纳分析，引出教学内容

由于本次课教学内容是可降阶的高阶微分方程，因此需要通过归纳分析微分方程式（3）的一般特点，进而引出教学内容。

首先，复习微分方程的“阶”的定义，并由此指出，该微分方程是一个高阶微分方程。事实上，根据前面的学习可知，微分方程的“阶”是指方程中未知函数的最高阶导数的阶数。具体到上述飞行轨迹方程，由于变量x是未知函数，而变量y是自变量，因此这个方程阶是2。

再进一步，在这个方程中除了未知函数的导数，只有自变量y而没有未知函数x。因此可以将其特点归纳为：不显含未知函数的二阶微分方程。其一般形式是

需要注意的是，在此过程中应提醒学生：尽管出于习惯，我们常常是把y看作未知函数，而把x看作自变量，但这不是必须的，例如在方程式（3）中就把变量x看作未知函数。

（四）  分析讨论，讲解求解方法

经过上述几个环节，大约使用8分钟时间完成了创设情境、建立模型和引出教学内容等步骤，接下来进入分析讨论、知识讲解环节。

首先从认识论认知心理学的角度看，当我们面对一个新问题时，往往首先考虑的借助与之相关的、已经掌握的方法来解决它。因此，对于高阶微分方程，一种自然也重要的思路是：将高阶微分方程的阶降低，转化为一阶微分方程，再来进行求解。

因此，接下来引导学员观察式（4）：由于方程中只出现了二阶导数，因此若把y′看作一个整体，用一个新的未知函数来代替它（即变量代换），例如令y′=p，则方程的阶就可以降低。

尝试令y′=p（x），并且两边同时对x求导数，可得

将式（5）代入原方程得到

至此可得到一个以x为自变量、以p为未知函数的一阶微分方程（6）。若该一阶微分方程能够利用已有知识求解，则直接求出它的通解，并记为p=φ（x，C1）。

再将引入的变量p代入上述通解，就可以得到

于是，两边同时求不定积分，就可完成微分方程的求解

最后，引导学生归纳出上述方法的数学思想和关键步骤。显然，上述求解过程的核心思想是“降阶”，即把高阶微分方程转化为我们更加熟悉的一阶微分方程。而关键步骤，也就是采取的核心手段是“变量代换”。事实上，变量代换是一种非常常用的转化问题的手段，我们在之前学习极限的计算、导数的运算和定积分的计算等内容时常常用到。在这里，变量代换法再次发挥了重要作用，为了进一步掌握这种方法，需要仔细分析总结这种方法的特点，并通过适当练习加以巩固。

为了帮助学生及时消化，可通过例题加以巩固。

例1 求解

解：分析方程特点可以发现，这是一个不显未知函数的二阶微分方程，可以按照上述方法求解。

令y′=p（x），则有

将其代入原方程，得到可分离变量的微分方程

求解该方程，得到p=C1（1+x2），即

再次两边同时求积分，得到微分方程的通解为

至此，大约使用28分钟将本次课的核心知识讲解完毕。接下来，可通过导弹飞行轨迹问题的解决，以及“降阶法”的提炼，进一步提升学员数学应用能力和数学思维。

（五）  回归问题，培养应用能力

例2 导弹飞行轨迹问题。

首先引导学员思考：根据前面的分析，虽然已经得到了导弹飞行轨迹满足的微分方程式（3），但由例1可知，若无其他条件，则只能求出通解，无法完全确定飞行轨迹。为此，需要找出问题的两个初值条件，才能求出通解中的两个常数，从而确定特解。

首先，在初始时刻，导弹位于坐标原点，所以当y=0时，x=0；其次，在初始时刻，空中目标位于点（3，4），而导弹速度方向始终指向空中目标，所以当x=0时，y′=4/3。再利用反函数求导法则，得到当y=0时，x′=3/4。于是，得到一个含有两个初值条件的二阶微分方程

显然，这个方程属于不显含未知函数x，因此可以按照上述求解方法进行求解。

令x′=p，两边同时对y求导数，得到x″=p。

代入到原方程，转化为

分离变量并对等式两端同时取不定积分，得到

由初值条件x′|y=0=，解得C1=4，即

对等式左端进行分子有理化，得到

将式（11）和式（12）两式相加，得到

将式（13）两端同时对y求不定积分，得到

由此，得到导弹运行轨迹方程为

在问题解决后，需要引导学员思考以下问题。

一是在上述求解过程中可以看到，要想求出二阶微分方程的特解，由于方程的通解中必然包含2个任意常数，因此需要利用2个初值条件来确定这2个常数的值。而在上述求解过程中，采取的是边积分边确定待定常数的方法，即得到式（10）后立即确定参数C2的值，得到式（14）后确定参数C1的值。事实上，在很多方程的求解过程中，边积分边确定常数的方法往往计算量更小。

二是在求解导弹追击空中目标的飞行轨迹时，我们是在“导弹始终指向空中目标”这一假定下完成的，事实上，这是一种十分重要的导引律，即“尾追法”。由此可见，微分方程在实际问题中有着重要应用。当然，随着技术的不断进步，“尾追法”这种制导律已逐渐被更先进的制导律所代替，因此需要我们持续不断地学习，才能在未来的工作中与时俱进，同时也鼓励学有余力的学生查阅“精确制导原理”等方面的书籍资料，了解更多导引律及其數学原理。

三是分析上述问题的解决过程可以发现，我们是先自行建立了实际问题的数学模型，从而得到了刻画该问题的微分方程，才能通过求解微分方程解决该问题。事实上，尽管我们在高等数学课程中，主要关注的是不同类型微分方程的求解方法，但在许多实际问题中，方程的建立往往比求解更为困难，甚至很多微分方程无法得到解析解。因此，为了将所学知识应用于未来的岗位实践中，既要始终关注和学习微分方程的建立过程，同时还要不断学习更多的数学类课程，如数理方程、微分方程数值解、有限元分析等。

综上所述，对于不显含未知函数的二阶微分方程，其求解的基本思路是通过变量代换来降低微分方程的阶，从而使二阶微分方程转化为两个一阶微分方程。这正是“降阶法”的核心思想。在求解过程中，关键步骤在于令y′=p（x），即降阶过程是通过变量代换来实现的。

四  结束语

该案例以导弹飞行轨迹问题为驱动，以求解高阶微分方程的降阶法为核心，通过创设情景、提出问题，引导讨论、建立模型，归纳分析、引出教学内容，分析讨论、讲解求解方法，回归问题、培养应用能力等五个环节，引导学员由浅入深地思考，并学习如何运用所学知识解决实际问题。需要指出的是，所建立的微分方程式（3）是以x为未知函数的，这与我们以y为未知函数的习惯略有不同。要解决这一问题，只需将x轴和y轴互换，并将背景设定为鱼雷追击潜艇即可。但考虑到实际中的微分方程并非必须把y视作未知函数，因此这样设定教学案例有助于帮助学生加深对微分方程的理解。此外，采用该案例进行教学通常比传统方法多出6～8分钟，考虑到培养学生数学应用能力的需要，笔者认为这是值得的。若条件允许，可以适当借助翻转课堂的方式，让学生提前适应案例内容，这也是笔者下一步研究的方向。

参考文献：

[1] 汪雄良，王春玲.高等数学课程研究型教学案例的构建与实践[J].中国教育技术装备，2016（4）：107-109.

[2] 李坤.本科数学专业课程中教学案例的创新探索[J].大学数学，2018，34（2）：116-120.

[3] 钱明辉，李天明，舒诗雅，等.教学案例开发框架模型的构建及其应用[J].管理案例研究与评论，2018，11（2）：201-220.

[4] 刘庆辉.基于常微分方程课程教学内容改革的思考与研究[J].成都师范学院学报，2017，33（5）：115-117.

[5] 郑苏娟.一元微积分中探究式的教学案例[J].高等数学研究，2022，25（1）：1-3，7.