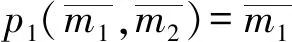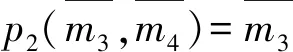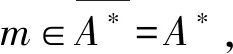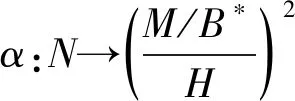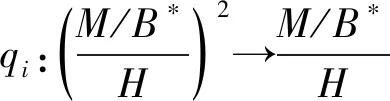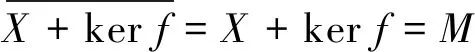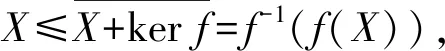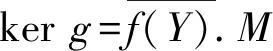Factor-square-full半模

王永铎, 鲁 靖

(兰州理工大学 理学院, 甘肃 兰州 730050)

半环[1]作为常见的代数结构,不但在拓扑学、分析学和最优化理论中有较广泛的应用,而且在计算机科学中有极其重要的地位.众所周知,在环论中用模[2]刻画环是研究环的有效途径.20世纪20年代,代数工作者就曾利用半环上的半模研究半环,得到了Jacobson根的结构定理.由于环上模都可以看成半环上半模,所以半模的研究很大程度上是对环上模的推广,进而许多基础数学和应用数学甚至计算机科学中的数学结构也可以认为是适当的半环上的半模,因此对半模的研究自然也是有必要的.然而,半模并不是模的简单推广,由于可换幺半群的性质比 Abel 群复杂,半环的结构比环松散,所以对半模的研究比模要困难得多.

Tuyen等[4]引入了多余子半模的定义.设M是半模,N≤M.称N是多余的,如果对M的任意子半模K,由N+K=M可推出K=M,记作N≪M.

Kikumasa等[5]引入了d-square子模,quasi-d-square子模,factor-square-full模的概念.设M是模.称M的真子模X是d-square,若存在满同态f:M→(M/X)2.称M的真子模X是quasi-d-square,若存在M的d-square子模Y,使得X≤Y.称M为factor-square-full模,若M的任意真子模是quasi-d-square.受文献[5-7]的启发,本文把d-square子模,quasi-d-square子模,factor-square-full模的概念推广到半模上,得到了一些新的结论.

本文中,S都是半环,M都是左S-半模.N≤M表示N是M的子半模.

1 半模上正规满同态的性质

引理1设M,N1,N2是半模,fi:M→Ni是正规满同态(i=1,2).考虑以下条件:

1)M=kerf1+kerf2;

2)φ:M→N1⊕N2是由φ(m)=(f1(m),f2(m))定义的满同态;

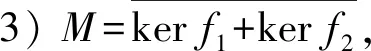
证明1)⟹2) 任取(n1,n2)∈N1⊕N2,因为fi是满同态,所以存在m1,m2∈M,使得f1(m1)=n1,f2(m2)=n2.又因为M=kerf1+kerf2,所以存在a1,a2∈kerf1,b1,b2∈kerf2使得m1=a1+b1,m2=a2+b2,则

φ(b1+a2)=(f1(b1+a2),f2(b1+a2))

因为b1+a2+a1=m1+a2,b1+a2+b2=m2+b1,分别用f1,f2作用于以上两式两端,得

f1(b1+a2)=f1(m1)=n1

f2(b1+a2)=f2(m2)=n2

所以b1+a2是(f1(m1),f2(m2))的原像,故φ为满同态.

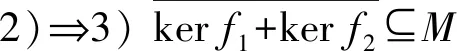
f1(m+k)=f1(m)+f1(k)=f1(k′)

其中f1(k)=f1(k′)=0.

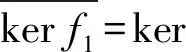
命题1设M,N是半模.若α:M→N是同态,A≤M,B≤N,则α(α-1(B))=B∩Imα.

证明“⊆” 任取b∈α(α-1(B)),则b∈Imα,且存在b′∈α-1(B)使得α(b′)=b,所以α(b′)∈B,因此b∈B∩Imα.

“⊇” 任取b∈B∩Imα,则有b∈B且b∈Imα.存在b′∈M使得α(b′)=b∈B,所以b′∈α-1(B),b∈α(α-1(B)).

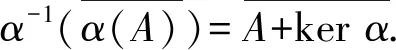
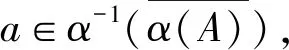
命题3设A,B,C是半模,α:A→B,β:B→C是同态.则

1) ker(βα)=α-1(ker(β));

2) Im(βα)=β(Im(α)).

证明1) 任取a∈ker(βα),当且仅当βα(a)=0,当且仅当α(a)∈kerβ,当且仅当a∈α-1(ker(β)).

2) Im(βα)=βα(A)=β(α(A))=β(Im(α)).

引理2设M,N是半模.若f:M→N和g:N→K都是正规满同态,则gf是正规满同态.

证明设gf(m)=gf(m′),其中m,m′∈M.因为g是核正规同态,所以存在n1,n2∈kerg,使得f(m)+n1=f(m′)+n2.因为f是满同态,所以n1,n2在M中分别存在原像a1,a2,使得f(a1)=n1,f(a2)=n2,则f(m)+f(a1)=f(m′)+f(a2),进而f(m+a1)=f(m′+a2).

因为f是核正规的,所以m+a1+kerf=m′+a2+kerf.因为f(a1)=n1∈kerg,所以a1∈ker(gf).由ker(f)⊆ker(gf)知a1+ker(f)⊆ker(gf).同理,a2+ker(f)⊆ker(gf).故gf是正规满同态.

证明因为f是满同态,所以是像正规的.下面只需证f是核正规的.

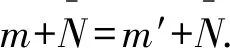
设M,N,X,Y是半模,f:M→N和g:X→Y都是半模同态.本文中f⊕g表示M⊕X→N⊕Y:(m,x)→(f(m),g(x)),其中m∈M,x∈X.

推论1设M是半模,N≤M.如果υ:M→M/N是自然满同态,那么υ⊕υ是正规满同态.

证明设(υ⊕υ)(m1,m2)=(υ⊕υ)(n1,n2),其中(m1,m2),(n1,n2)∈M2.因为υ是正规满同态,所以对于υ(m1)=υ(n1),存在k1,k′1∈kerυ,使得m1+k1=n1+k′1.同理,存在k2,k′2∈kerυ,使得m2+k2=n2+k′2,所以(m1,m2)+(k1,k2)=(n1,n2)+(k′1,k′2),其中 (k1,k2),(k′1,k′2)∈ker(υ⊕υ),因此υ⊕υ是正规满同态.

推论2设N1,N2是半模.如果π1:N1⊕N2→N1是由π1(n1,n2)=n1定义的标准投影,那么π1是正规满同态.

证明设π1(n1,n2)=π1(n′1,n′2),其中(n1,n2),(n′1,n′2)∈N1⊕N2,则n1=n′1,进而(n1,n2)+(0,n′2)=(n′1,n′2)+(0,n2),其中(0,n2),(0,n′2)∈0⊕N2=kerπ1,所以半模上的标准投影是正规满同态.

引理4设M,N是半模.如果f:M→N是正规满同态,那么存在从M/kerf到N的同构.

证明因为f是满同态,所以存在由g(m+kerf)=f(m)定义的半同构g:M/kerf→N.设f(m1)=f(m2),其中m1,m2∈M,因为f是正规的,所以m1+kerf=m2+kerf,因此g是单的.故g是同构.

命题4设M,N是半模,f:M→N为正规满同态,M的subtractive子半模的和是subtractive,M′≤M.如果M′是M的subtractive子半模,那么f(M′)是subtractive子半模.

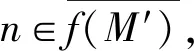
f(m)+f(m1)=f(m+m1)=f(m2)

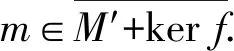
2 factor-square-full 半模

定义1设M是半模,X是M的真subtractive子半模.如果存在正规满同态f:M→(M/X)2,那么称X是M的d-square子半模.

例1自然数集N构成半环,N是N上的半模,则N⊕0是N2的 d-square 子半模.

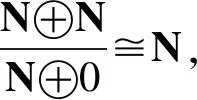
定义2设M是半模,X是M的真subtractive 子半模.如果存在M的d-square子半模Y,使得X≤Y,那么称X是quasi-d-square.

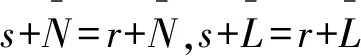
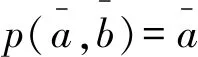
证明“⟸” 由quasi-d-square 子半模的定义可得.

“⟹” 设X是M的quasi-d-square子半模,则由定义知存在M的d-square子半模Y,使得X≤Y且f:M→(M/Y)2是正规满同态.

令qi:(M/Y)2→M/Y是标准投影(i=1,2),通过φ(m)=(q1f(m),q2f(m)) 定义φ:M→M/Y×M/Y,其中m∈M.由引理2和推论2知qif是正规满同态.因为M的subtractive子半模的和是subtractive,由引理1知M=ker(q1f)+ker(q2f).

如果Y+ker(q1f)

设π:M/Y→M/A,g1:M→M/A是自然满同态,g2=πq2f,则

ker(g1)=A, ker(g2)=ker(πq2f)

因为

所以

M=ker(g1)+ker(g2)

由引理1,通过φ1(m)=(g1(m),g2(m))定义的φ1:M→(M/A)2为满同态.设g1(m)=g1(m′),g2(m)=g2(m′),其中m,m′∈M.由引理2,引理3和推论2知g1,g2是核正规的,所以m+kerg1=m′+kerg1,m+kerg2=m′+kerg2.因为M满足陪集条件,所以

m+kerg1∩kerg2=m′+kerg1∩kerg2

如果Y+ker(q1f)=M.令h1:M→M/Y是自然满同态,h2=q1f.因为Y=ker(h1),ker(h2)=ker(q1f),所以M=ker(h1)+ker(h2).

定理2设M是半模,A≤B≤M.则

1) 如果B是M的quasi-d-square子半模,那么A是M的quasi-d-square子半模;

2) 如果B/A≪M/A,B是M的真subtractive子半模,M的subtractive子半模的和是subtractive,A是M的quasi-d-square子半模,那么B是M的quasi-d-square子半模.

证明1) 由 quasi-d-square 子半模的定义可得.

2)B是M的真subtractive子半模.因为A是M的quasi-d-square子半模,所以存在M的d-square子半模A*,使得A≤A*,且φ:M→(M/A*)2是正规满同态,其中m1,m2∈M.

当A*=M结论自然成立.下证当A*

设υ:M/A*→M/(B+A*) 是自然满同态.由引理2和推论1知 (υ⊕υ)φ:M→(M/(B+A*))2是正规满同态.所以B+A*是M的d-square子半模.又因为B≤B+A*,所以B是M的quasi-d-square子半模.

定理3设M,N是半模,f:M→N是正规满同态,M满足陪集条件.则

1) 如果A是N的quasi-d-square子半模,那么f-1(A)是M的quasi-d-square子半模;

2) 如果kerf≪M,M的subtractive子半模的和是subtractive,B是M的quasi-d-square子半模,那么f(B)是N的quasi-d-square子半模.

证明1) 任取a,a′∈f-1(A),s∈S.因为f(a),f(a′)∈A,所以sf(a)∈A,则f(sa)∈A,进而sa∈f-1(A).又因为f(a)+f(a′)=f(a+a′)∈A,a+a′∈f-1(A),所以f-1(A)是M的子半模.

因为A是N的quasi-d-square子半模,所以存在N的d-square子半模A*,使得A≤A*,φ:N→(N/A*)2为正规满同态.当A*=N结论自然成立.下证当A*

设υ:N/A*→M/f-1(A*)的对应法则为υ(f(m)+A*)=m+f-1(A*),其中m∈M.若m1,m2∈M,f(m1)+A*=f(m2)+A*,则存在a3,a4∈A*使得f(m1)+a3=f(m2)+a4.

令a3=f(b),a4=f(b′),其中b,b′∈f-1(A*),则f(m1)+f(b)=f(m2)+f(b′),进而f(m1+b)=f(m2+b′).因为f是核正规的,所以存在k,k′∈kerf,使得

m1+b+k=m2+b′+k′

因为b+k,b′+k′∈f-1(A*)+kerf⊆f-1(A*),所以m1+f-1(A*)=m2+f-1(A*),故υ是映射.

因为

且

所以υ是同态.

因为对任意的m+f-1(A*)∈M/f-1(A*),都能在N/A*中找到原像f(m)+A*,所以υ是满的.

设m+f-1(A*)=m′+f-1(A*),其中m,m′∈M.存在b,b′∈f-1(A*)使得m+b=m′+b′,用f作用于等式两端,

因为f(b),f(b′)∈A*,所以

f(m)+A*=f(m′)+A*

所以υ是单的.因此υ是同构.由定理2和推论1知(υ⊕υ)φf是正规满同态.

因为A≤A*,所以f-1(A)≤f-1(A*).假设f-1(A*)=M,由命题1知:

f(f-1(A*))=A*∩Im(f)=A*∩N=A*

因为f(M)=N,所以N=A*,但是这与A*

2) 因为M的subtractive子半模的和是subtractive,B是M的quasi-d-square子半模,由定理1知存在M的真subtractive子半模B*,由ψ(m)=(m1+B*,m2+B*)定义的正规满同态ψ:M→(M/B*)2使得B≤B*,且p1ψ是正规满同态,其中m1,m2∈M,pi:(M/B*)2→M/B*是第i个位置的标准投影(i=1,2).

令H=p1ψ(kerf)+p2ψ(kerf),由命题4知H是subtractive子半模.设存在L≤M,使得p2ψ(kerf)=L/B*,且L是subtractive子半模.由引理2知p2ψ是核正规的.如果L/B*=M/B*,那么由命题2知:

因为

(p2ψ)-1(M/B*)=M

所以

因为kerf≪M,所以ker(p2ψ)=M,进而p2ψ(M)=0,但是这与M/B*≠0矛盾,因此L/B*

(ρ⊕ρ)ψ(m)=(ρ(a+B*),ρ(b+B*))=(0,0)

进而kerf⊆ker((ρ⊕ρ)ψ).由引理2和推论1,(ρ⊕ρ)ψ是正规满同态.由引理4,

因为

定义3设M是半模.如果M的任意真subtractive子半模是quasi-d-square,那么称M是factor-square-full半模.

定理4设M,N是半模,f:M→N为正规满同态,kerf≪M,M满足陪集条件且subtractive子半模的和是subtractive.则M是factor-square-full半模当且仅当N是factor-square-full半模.

证明“⟹” 任取N的真subtractive子半模Y,则f-1(Y)≤M.若

f-1(Y)=M={m∈M|f(m)∈Y}

则Y=N,但是这与Y

故

定理5设M是半模,M满足陪集条件且subtractive子半模的和是subtractive.则以下等价:

1)M是 factor-square-full 半模;

2) 对M的任意真subtractive子半模X,存在M的真subtractive子半模Y,正规满同态f:M→(M/Y)2,使得X≤Y,且pf是自然满同态,其中p:(M/Y)2→M/Y;

3) 对M的任意真subtractive子半模X,存在M的真subtractive子半模Y,Z,使得X≤Y,M=Y+Z且M/Y≅M/Z;

4) 对任意的非零的正规满同态f:M→A,存在半模B,正规满同态g:A→B,M的真subtractive子半模Z,使得kergf+Z=M,M/kergf≅M/Z.

证明1)⟹2) 因为M满足陪集条件,所以由定理1知2)成立.

2)⟹3) 由2),f:M→(M/Y)2是正规满同态.设pi:(M/Y)2→M/Y是第i个位置的标准投影(i=1,2),f1=p1f是自然满同态,f2=p2f,kerf2=Z.因为Y=ker(p1f),所以由引理1知M=Y+Z且M/Z=M/kerf2.因为f2是正规满同态,所以由引理4,

M/kerf2≅Imf2=M/Y

因此M/Z≅M/Y.

3)⟹4) 设f:M→A是正规满同态.若kerf=M,则A=0,但是这与f非零矛盾,因此kerf

M=kergf+Z,M/Z≅M/Y≅M/kergf.

4)⟹1) 任取M的真subtractive子半模X,f:M→M/X是自然满同态.由4)知,存在半模B,正规满同态g:M/X→B,M的真subtractive子半模Z,使得

kergf+Z=M,M/kergf≅M/Z

令φ:M→M/(kerf∩Z) 是自然满同态,则

X=kerf⊆kergf

通过α(z+kergf∩Z)=z+kergf定义α:Z/(kergf∩Z)→(kergf+Z)/kergf.设α(z1+kergf∩Z)=α(z2+kergf∩Z),其中z1,z2∈Z.则z1+kergf=z2+kergf,存在k1,k2∈kergf使得α(k1+kergf∩Z)=k1+kergf=0+kergf,α(k2+kergf∩Z)=0+kergf,所以k1+kergf∩Z,k2+kergf∩Z∈kerα满足:

因此α是核正规的.

因为

所以

因此δ:M→(M/kergf)2是正规满同态,故M是factor-square-full半模.

命题5如果M是subtractive半模,那么M(I),MI是factor-square-full 半模,其中I是至少包含两个元素的指标集.

证明假设I={1,2,…,n}是有限集,采用归纳法.

若n=2,令M1=M×0,M2=0×M,设pi:M2=M1×M2→Mi是到第i个位置的标准投影,其中i=1,2.设α:M1→M2是由α(m,0)=(0,m)定义的同构.

任取M2的真subtractive子半模X.如果p1(X)≠M1,由命题4,p1(X)是subtractive子半模.令Y=p1(X)⊕M2,Z=M1⊕α(p1(X)),则Y,Z是M2的真subtractive子半模,并满足X≤Y,M2=Y+Z.

设P1(X)=N×0.因为

所以M2/Y≅M2/Z.

否则P1(X)=M1,M2=X+M2.令K=α-1(X∩M2)⊕M2.若X∩M2=M2,则M2≤X,P1(X)=M.任取(m1,m2)∈M2,(m1,a),(0,m2),(0,a)∈X,则

(m1,m2)+(0,a)=(m1,a)+(0,m2)

因此M2≤X,但是这与X

若n≥2,假设Mn是factor-square-full半模,考虑n+1的情形.

令M1=M×0×…×0,设q:Mn+1=M×Mn→Mn是标准投影,β:M1→M是同构.任取Mn+1的真subtractive子半模X′,若q(X′)≠Mn,如果Mn是factor-square-full半模,那么存在Mn的真subtractive子半模A,B使得q(X′)≤A,Mn=A+B,Mn/A=Mn/B.令Y′=M×A,Z′=M×B,则Y′,Z′是Mn+1的真subtractive子半模,且满足:

X′≤Y′,Mn+1=Y′+Z′,Mn+1/Y′≅Mn+1/Z′

否则,Mn+1=M1+X′.令K′=M×β(M1∩X′)×M×…×M.因为M1∩X′是真subtractive子半模,所以K′是真subtractive子半模.因为Mn+1=X′+K′,Mn+1/X′≅Mn+1/K′,所以Mn+1是 factor-square-full 半模.

假设I是无限集,有M(I)≅(M(I))2,MI≅(MI)2,所以M(I),MI是factor-square-full半模.