基于1D-LeNet-5模型的滚动轴承故障诊断方法

郭俊锋, 孙 磊, 王淼生,续德锋

(兰州理工大学 机电工程学院, 甘肃 兰州 730050)

在风电机组中,滚动轴承作为支撑回转零件发挥着重要作用.风电机组的滚动轴承经常在高负载、恶劣环境和无休状态下工作,从而需要高效的现场维护.由于技术水平和风场条件等因素制约,所以多采用定时检修的方法进行运维.然而,即使投入大量人力也无法精确定位故障[1].因此,通过状态检测对发生故障征兆或已发生故障的轴承进行维护和故障诊断被愈发重视.

滚动轴承故障诊断方法可分为基于分析模型的方法、基于知识推理的方法和基于数据驱动的方法.早期故障诊断大多采用动力学建模,针对特定工况该方法具有十分不错的效果.Kogan等[2]基于赫兹弹性接触理论,分析了滚动轴承动力学特性,建立了三维球轴承动力学模型,并在外圈轴向变形的角接触球轴承上验证了模型的可靠性.王凯等[3]针对复合故障激励的滚动轴承,提出了四自由度复合故障深沟球轴承的动力学模型,分析了3种工况下滚动轴承复合故障对系统动力学振动响应的影响.然而,基于模型的故障诊断方法只适用于特定工况,工况变化后要重新建立复杂的动力学模型.随着计算机技术的发展,各种频谱分析从理论变为现实,更多的现代信号分析与处理技术在故障诊断中得以应用.An等[4]提出了基于变分模态分解(VMD)和奇异值分解(SVD)的故障诊断方法,将得到的奇异值作为故障特征向量,能有效识别风电机组滚动轴承的故障.郑近德等[5]提出了自适应经验傅里叶分解(AEFD),能够有效地识别故障,而且识别效果优于经验模态分解(EMD),但其中边界集的设置有待进一步研究.在实际应用中,基于信号处理的方法大多需要人工选取特征,过程比较繁琐.随着人工智能的发展,基于大数据驱动的机器学习方法被广泛应用于滚动轴承状态监测和故障诊断.支持向量机(support vector machine,SVM)[6]、BP神经网络(back propagation neural network,BPNN)[7]和K近邻法(K-nearest neighbor,KNN)[8]等已被广泛应用于故障诊断,并取得了较好的效果.传统的机器学习方法因网络结构较浅而导致特征提取能力不足,需要通过人工选择特征,并且难以自适应挖掘和提取隐藏于故障数据中更深层次的特征.深度学习方法的提出给故障诊断研究带来了新思路,卷积神经网络(convolutional neural etwork,CNN)是其中很有效的深度学习方法.Kumar等[9]提出了稀疏深度学习方法,在CNN模型中引入稀疏正则化,能够识别不同转速条件下的轴承和转子故障.Shen等[10]提出了将阈值模型与CNN结合并基于物理信息的故障诊断方法,提高了滚动轴承故障诊断准确率.但是,这些CNN模型网络层次较深,需要逐层改动参数,容易造成过拟合,影响模型性能,并且对计算机的计算能力要求较高.

Lecun等[11]在1998年提出了LeNet-5模型,该模型对于识别手写体的分类具有很大优势,也成功应用于汽车雷达检测[12]、交通标志识别[13]等领域.然而,基于LeNet-5模型的轴承故障诊断方法存在识别精度低、收敛速度慢、泛化能力弱等问题.相比LeNet-5模型,1D-LeNet-5模型的卷积窗口更大,计算代价更小,速度更快[14].Wan等[15]提出了深度LeNet-5模型,网络层数较深,并且引入人工蜂群算法(artificial bee colony algorithm,ABC算法)改进模型参数;但该方法训练参数多,模型复杂,且准确率较低.

本文对LeNet-5模型进行优化改进,提出改进的一维卷积神经网络轴承故障诊断方法,训练时间较短,且呈现出更稳定、更准确的分类效果.首先,对轴承的原始振动信号进行预处理,利用短时傅里叶变换转化为灰度图像,即包含丰富时频信息的时频图,从而生成相应的数据集;然后,将数据集作为1D-LeNet-5模型的输入对其进行训练;最后,利用训练后的模型进行故障诊断.

1 基本理论

1.1 LeNet-5模型

LeNet-5模型结构由输入层、2个二维卷积层(分别称之为卷积层1、卷积层2)、2个二维池化层(分别称之为池化层1、池化层2)、2个全连接层(分别称之为全连接层1、全连接层2)和输出层组成,如图1所示,它是其他深度学习模型的基础.至今,LeNet-5模型及其改进模型,仍然在人工智能领域被广泛应用.图1中:输入为32×32的灰度图;卷积层1使用6个大小为5×5的卷积核,输出6个大小为28×28的特征图;池化层1对卷积层1的输出进行2×2最大池化操作,输出6个大小为14×14的特征图;卷积层2使用16个大小为5×5的卷积核,输出16个大小为10×10的特征图;池化层2对卷积层2的输出进行2×2最大池化操作,输出16个大小为5×5的特征图;全连接层1有120个神经元,与池化层2全连接,并生成120个1×1的特征图;全连接层2有84个神经元,生成84个1×1的特征图.由于LeNet-5模型最早被应用于手写数字识别任务,所以输出层有10个神经元,可以划分10个不同的类别.

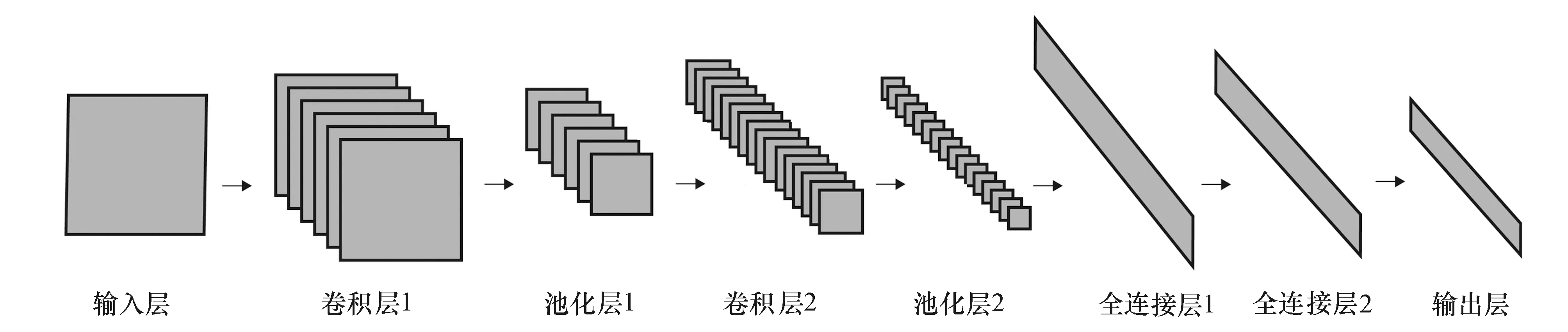
图1 LeNet-5模型结构

LeNet-5模型卷积层的卷积核为二维卷积形式,即

g(x-τ1,y-τ2)dτ1dτ2

(1)

式中:x、y为2个不同维度(方向)的变量;f(x,y)和g(x,y)为2个表征函数;τ1、τ2为2个不同维度上遍历的量.

在图像处理中,实际意义是将卷积核翻转,之后在被卷积对象上沿2个方向平移,生成的结果由卷积核在各个位置的计算结果组成.

二维卷积的离散形式为

g(x-n1,y-n2)

(2)

式中:n1、n2为2个不同维度的离散点.

卷积核的每个元素与被卷积对象对应位置相乘求和,得到卷积结果.

1.2 1D-LeNet-5模型

LeNet-5模型虽然在图像处理中具有良好的效果,但是多层二维卷积和池化操作导致训练时间长,收敛速度慢,并且复杂的计算过程对计算机硬件要求高.相比二维卷积神经网络,一维卷积神经网络的卷积核维度低,可以使用更大的卷积窗口,计算速度更快,代价更低.

一维卷积的形式为

(3)

式中:τ为一维方向上遍历的量.

一维卷积的卷积核f(τ)以τ为中心,在g(x)上沿1个方向进行滑动窗口移动,卷积核的每个元素与被卷积对象对应位置相乘求和.本文所提1D-LeNet-5模型设计了2个卷积层、2个池化层和2个全连接层,如图2所示.同时,展平层被用于池化层与全连接层的过渡,加入泄露修正线性单元(leaky rectified line unit,Leaky-ReLU)激活函数、Dropout层、批归一化(batch normalization,BN)层以提高模型的鲁棒性.

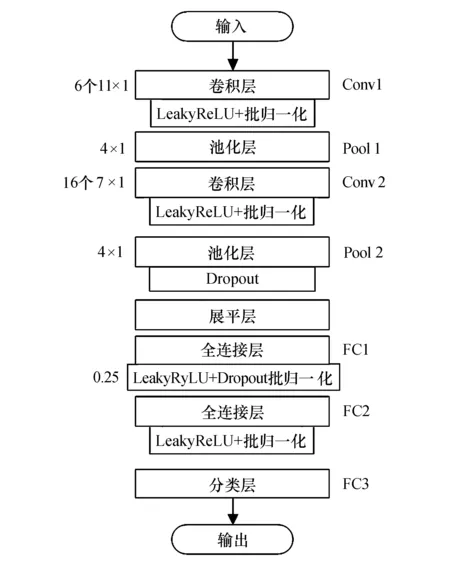
图2 1D-LeNet-5模型结构

模型参数和输出尺寸如表1所列.模型输入为32×32大小的图像,本文针对10类轴承进行分类,输出大小为10×1.每个卷积层采用不同数量和大小的卷积核,根据经验,Conv1层采用6个大小为11×1 的卷积核,Conv2层采用16个大小为7×1的卷积核,取步长为1进行一维卷积运算.

表1 1D-LeNet-5模型的参数

采用不同大小的池化核建立模型,分别进行7次训练,对训练时长的影响如图3所示.可以看出:采用4×1的池化核时,平均耗时为33.71 s;采用2×1的池化核时,平均耗时为36.01 s,可能是由于池化核越小计算量越大;采用6×1大小的池化核时,平均耗时为36.25 s,可能是由于池化核过大特征提取不明显,从而不能及时完成训练.因此,Pool1层和Pool2层执行4×1的最大池化操作,步长为4.

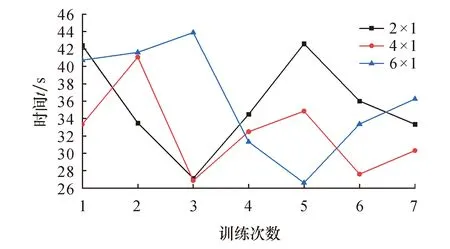
图3 不同池化核大小对训练时长的影响

设模型训练迭代次数为20,选取常用激活函数进行训练,对测试集准确率的影响如图4所示.可以看出:当使用sigmoid激活函数时,测试集准确率较低,训练20次后准确率为38%左右;ReLU函数的表现虽然较好,但是经过20次训练后不够稳定;选用常数为0.2的LeakyReLU激活函数进行训练最终可以达到准确率99%,在第10次训练之后,LeakyReLU激活函数明显更加稳定.因此,在模型相应位置加入LeakyReLU激活函数,依据经验取系数alpha为0.2,增加对特征细节的处理.

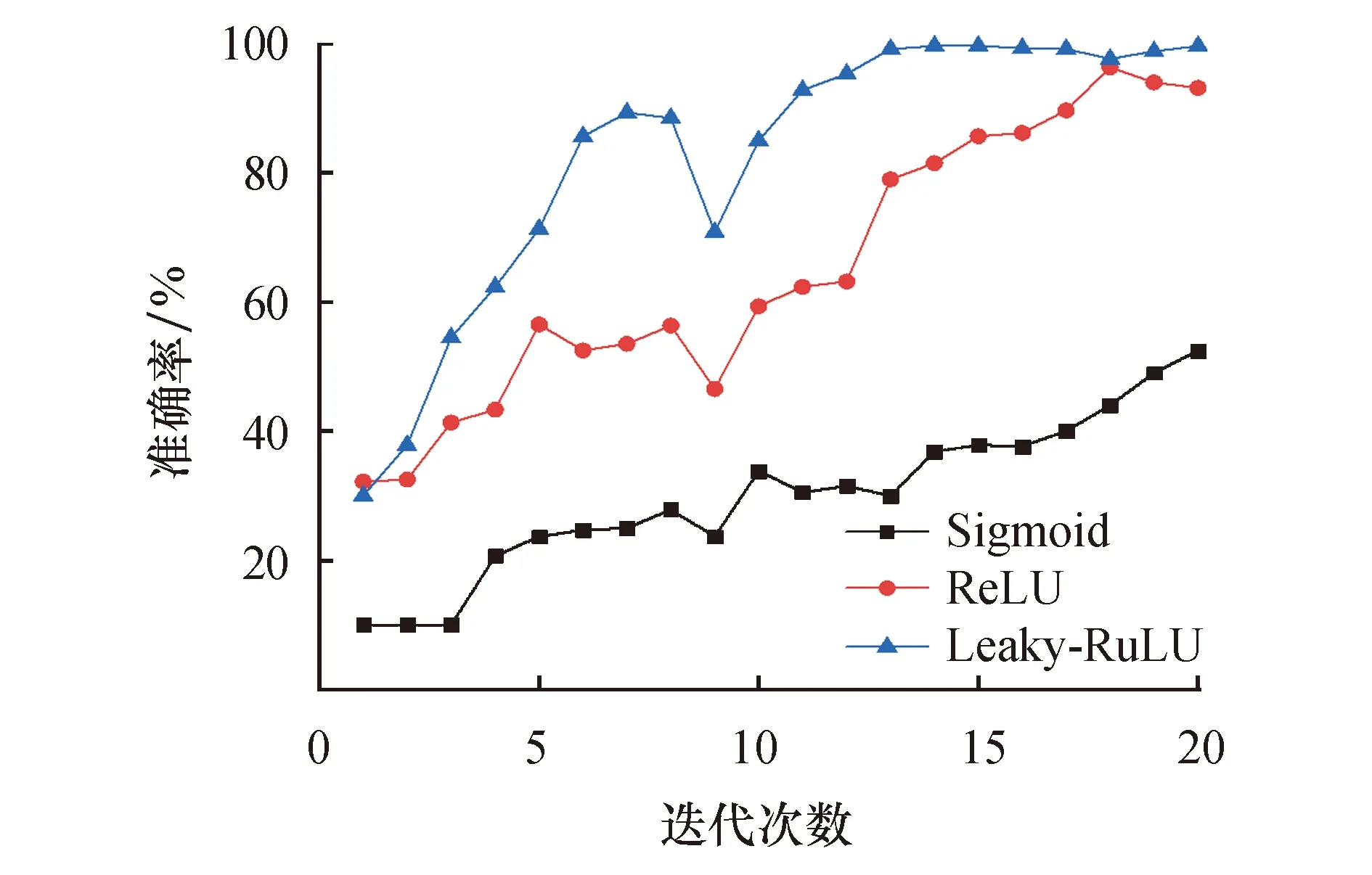
图4 不同激活函数对测试集准确率的影响

图5为不同丢失率的训练结果.可以看出,加入Dropout操作后,随着训练迭代,模型在验证集的训练不仅收敛速度变快,而且稳定性更强,同时也防止了过拟合现象.不同的丢失率只对最开始的若干次训练有影响,经过20次训练后都能使模型测试集准确率达到99%左右.为充分获取样本集特征,设Dropout率为0.25.

图5 不同丢失率对测试集准确率的影响

图6为加入BN层对测试集准确率的影响.可以看出:不加入BN层训练20次后,测试集分类准确率为80%左右,在第18次迭代结束时,达到最高值91%左右,模型准确率低且不稳定;加入BN层,在第11次迭代后,测试集分类准确率保持在95%以上,相比之下准确率更高,收敛速度更快,模型更稳定.因此,在全连接层后引入BN层,依据经验设参数momentum为0.8.

2 基于1D-LeNet-5模型的轴承故障诊断方法

为了实现对轴承故障信号的特征提取和故障分类,本文对原始振动信号进行短时傅里叶变换,生成灰度图像,即时频图,包含丰富的时频信息,能更大程度地获得故障信息.短时傅里叶变换为

(4)

式中:u为时间;ω为角频率;z(u)为时域信号;r(u-t)为中心位于t的时间窗口.

灰度图像只有1个颜色通道,以2D张量存储可作为1D-LeNet-5模型的输入.将生成的时频图随机划分为训练集和测试集,利用训练集对1D-LeNet-5模型进行训练.在训练结束后,将测试集输入训练后的模型,由模型输出的准确率来确定模型的诊断精度和鲁棒性.故障诊断流程如图7所示,具体步骤如下:

1) 采集轴承振动原始信号;

2) 对原始数据进行短时傅里叶变换,获得时频图像;

3) 将得到的图像按6.5∶3.5的比例分为训练集和测试集;

4) 利用训练集的样本训练1D-LeNet-5模型,得到故障诊断模型;

5) 对训练后的故障诊断模型进行测试;

6) 输出故障诊断结果.

3 实验验证分析

3.1 实验数据集说明

本文的实验数据集来自凯斯西储大学的轴承开放数据集.在实验中,轴承负载均为1 HP,采样频率为12 kHz,故障直径分别为0.177 8、0.355 6、0.533 4 mm.故障位置分别为内圈、滚动体和外圈,选取正常状态的轴承信号,共组成10组数据,对每类故障状态进行编号,如表2所列.

表2 数据标签划分

原始振动信号经短时傅里叶变换后的时频灰度图像如图8所示.

图8 短时傅里叶变换后的时频图

本文对原始数据进行重叠采样生成200张包含时频信息的灰度图像,并将200张时频图按照13∶7随机分成训练集和测试集.如表2所列,从每类故障状态的时频图中,随机选择出130个样本组成训练集,剩余70个样本组成测试集,共计1 300个样本训练集和700个样本测试集.

3.2 实验验证

通过故障诊断实验验证本文所提模型的有效性和优越性.对LeNet-5模型和1D-LeNet-5模型依次进行训练,其中,梯度下降样本数(batch_size)为100,迭代次数(epochs)为20次.在每次迭代训练结束后观察测试集测试分类准确率和损失值.准确率反映预测类别与真实类别的一致程度,损失值反映模型预测值与真实值之间的差距,如图9所示.图9a为测试集在2种模型的准确率对比,图9b为测试集在2种模型的损失值对比.可以看出:LeNet-5模型训练效果并不稳定,在迭代至第19次时效果最好,但不能保持下去,鲁棒性不强;1D-LeNet-5模型在迭代至第7次左右训练准确率接近100%,并能保持至训练结束;同时,损失值最终趋于0,表示预测值十分接近目标值.由此说明,本文所提模型的鲁棒性较强.

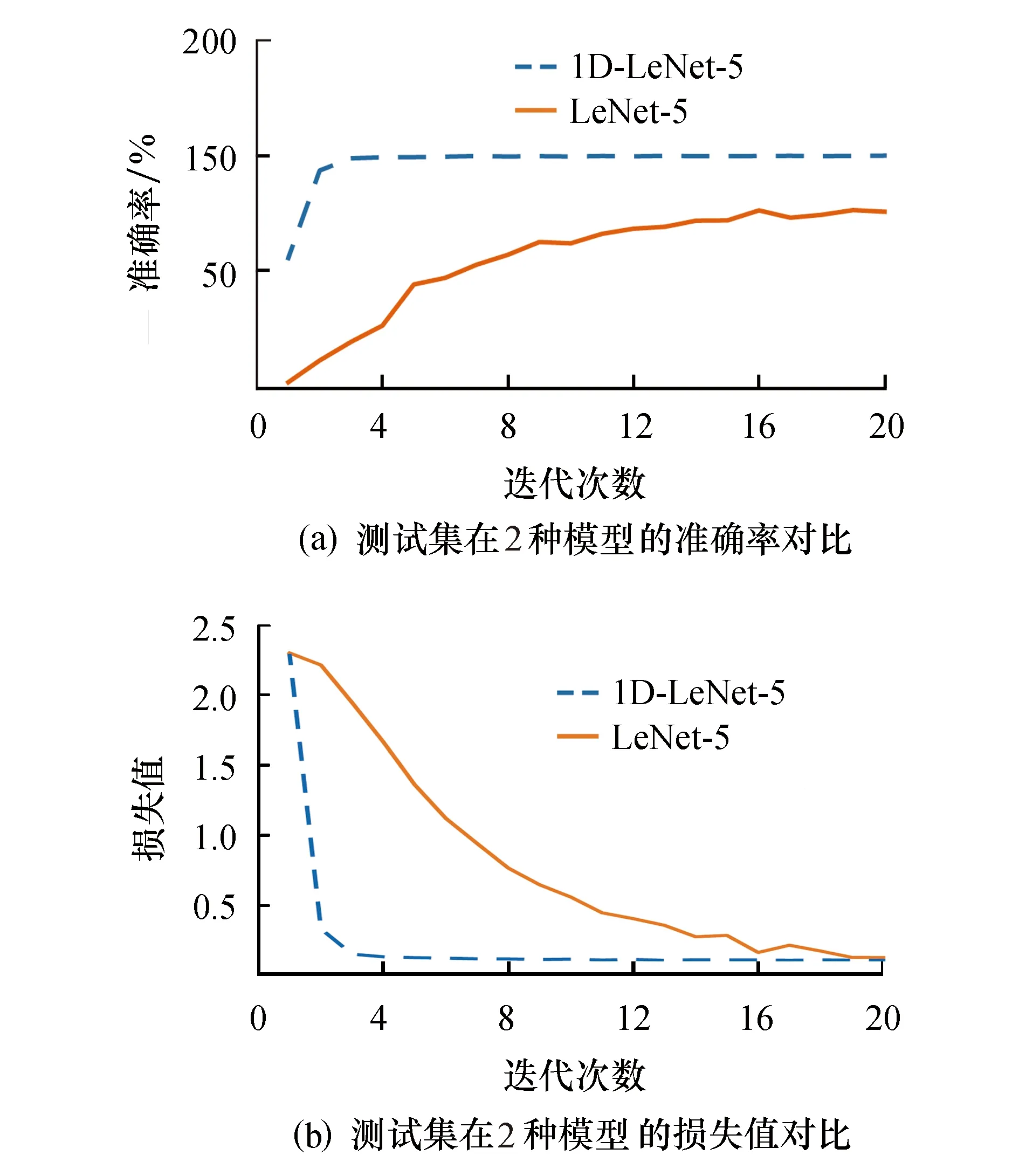
图9 测试集的准确率和损失值

为了直观地验证1D-LeNet-5模型分类性能的优越性,将该模型与深层网络模型如多层感知器(multilayer perceptron,MLP)、LeNet-5模型进行对比.采用t-邻近(t-SNE)算法对短时傅里叶变换、MLP、LeNet-5模型、1D-LeNet-5模型提取的深层次特征进行可视化分析.t-SNE算法是Hinton和Maaten在2008年提出的非线性降维算法[16],可以将高维数据降维到二维或三维,用于数据可视化具有很好的效果.t-SNE算法利用点与点之间相似度的概率分布进行聚类,形成特征簇以反映分类效果.在降维计算中,各簇第1个点随机分布在低维坐标系内,各簇分布位置随机,而各簇的紧密程度决定分类效果的优劣,如图10所示.其中,图10a为原始振动信号短时傅里叶变换后测试集提取特征的可视化结果,可以看出,短时傅里叶变换的特征提取能力有一定局限性,对于有些相似故障无法成功区分;图10b为MLP训练后测试集提取特征的可视化结果,可以看出,有些故障类别之间仍存在混淆,无法有效区分;图10c为LeNet-5模型训练后测试集提取特征的可视化结果,可以看出,对滚动体故障(Ball1、Ball2、Ball3)识别不够清晰,整体效果也略差;图10d为1D-LeNet-5模型训练后测试集提取特征的可视化结果,可以看出,每类故障样本特征簇聚类程度高,且无误判情况发生.因此,1D-LeNet-5模型的故障分类效果非常好.

图10 测试集在不同模型的特征可视化

为了进一步验证本文所提模型在故障诊断方面的优越性,选取若干浅层网络模型、深层网络模型与本文所提模型进行对比.使用表2所列的数据集,选取SVM、随机森林(random forest,RF)、决策树(decision tree,DT)、MLP、LeNet-5模型与本文所提模型进行故障诊断对比实验.模型输入均为经短时傅里叶变换后的时频图像,且输入数据相同.每个模型进行15次分类实验,测试集的平均故障分类准确率和标准差如图11所示.可以看出:3种浅层机器学习模型中DT和RF平均准确率低于SVM,这表明DT和RF不能实现很好的故障诊断效果;虽然SVM的故障诊断平均准确率达到95.1%,但是仍低于本文所提模型,这可能是由于传统的浅层机器学习模型不能挖掘数据深层次的特征信息;此外,虽然MLP取得了94.5%的故障诊断平均准确率,但是仍低于LeNet-5模型和1D-LeNet-5模型,这表明相对于卷积神经网络全连接神经网络在特征提取方面稍显不足;相比LeNet-5模型1D-LeNet-5模型取得了99.8%的故障诊断平均准确率,这是因为1D -LeNet-5模型具有较大尺寸的卷积核,使其在特征提取方面有更大的卷积视野,并且1D-LeNet-5模型中加入的批归一化层可以提高收敛速度,同时1D-LeNet-5模型的标准差表现也优于其他模型.综上所述,本文所提模型鲁棒性较强,可在实际应用中取得非常好的效果.

为了进一步验证1D-LeNet-5模型在轴承10种工作状态的表现,选取每种接近平均准确率的训练模型,引入多分类混淆矩阵对诊断结果细节进行分析.混淆矩阵能全面反映不同故障类型的诊断准确率和误判情况,通过对比预测标签与真实标签可以很清晰地看出混淆误判标签的真实故障情况,如图12所示.图中,x轴表示故障的预测类别,y轴表示故障的真实类别,主对角线上的数字表示1D-LeNet-5模型对每类故障测试集的诊断准确率.图12a～c分别为SVM、DT和RF这3种浅层机器学习模型训练后的混淆矩阵,可以看出,误判情况较多;图12d为MLP训练后的混淆矩阵,可以看出,混淆较多,效果略差;图12e为LeNet-5模型训练后的混淆矩阵,可以看出,其对滚动体故障(Ball1、Ball2、Ball3)识别误差较大;图12f为1D-LeNet-5模型训练后的混淆矩阵,可以看出,本文所提模型在每种故障类型都取得了极高的诊断准确率.各模型的混淆矩阵表现与上文可视化分析一致,这说明本文所提1D-LeNet-5模型在各故障类型都具有较高的故障识别率和较好的鲁棒性.

4 结论

针对现有基于深度学习的轴承故障诊断方法结构复杂、参数众多、训练困难的问题,本文提出了基于1D-LeNet-5模型的轴承故障诊断方法.该方法设计了稳定的一维网络结构,加入了Leaky-Relu激活函数、BN层和Dropout操作,得到了鲁棒性较强的1D-LeNet-5网络模型.对所采集轴承振动信号进行短时傅里叶变换,利用变换后训练集的样本训练模型并验证其准确率.

本文的主要贡献如下:

1) 设计了1D-LeNet-5网络模型,并对结构进行优化,提高了模型的鲁棒性;

2) 利用短时傅里叶变换预处理信号,充分获取信号在时频域的信息,更大程度地挖掘一维卷积神经网络的计算力;

3) 对池化核进行选取设计,提高了网络性能;

4) 加入Leaky-ReLU激活函数,在负输入值等细节处理上增加优势,减少了ReLU的稀疏性,增强了神经网络模型的非线性拟合能力,在克服梯度消失问题的同时加快训练速度;

5) 增加批归一化层和Dropout层,在提高算法收敛速度的同时,也提高网络泛化性能,同时防止模型过拟合.

利用凯斯西储大学的轴承开放数据集进行验证,结果表明,本文所提模型可以稳定、高效地完成10类故障的分类任务,且分类准确率和鲁棒性相对其他方法有一定程度的提升.

因此,本文所提方法通过振动信号实现轴承故障诊断具有一定的优越性,接下来可进一步探讨本文所提方法在风电机组轴承故障诊断中不同工况的使用效果.