基于改进迁移矩阵法的滚珠丝杠横扭耦合振动研究

吴 沁, 罗殿立, 杨冉冉

(兰州理工大学 机电工程学院, 甘肃 兰州 730050)

目前滚珠丝杠进给系统因其高精确度和高稳定性而被广泛应用于各种机床和驱动装置中,不仅如此,它还经常被应用在高速进给环境中.但是高速运动势必会造成滚珠丝杠的机械振动,对系统传动精度造成严重影响.因此,分析滚珠丝杠本体的振动特性是十分有必要的[1].

国内外对于连续体振动特性的分析主要采用近似离散化的方法:一种是对研究的连续系统根据边界条件施加一些合理约束,将系统各种位移假设成各自所对应的基函数与其所对应广义坐标的乘积,从而使无限维自由度的连续系统变为有限维自由度,其中使用最频繁的方法为Ritz级数法;另一种是将连续体的质量以合适的比例集中到有限个质点上,质点之间采用无质量的弹性元件进行连接,由此便将连续系统近似为有限维自由度系统,其中使用最频繁的是迁移矩阵法[2].迄今为止,对于工作过程的滚珠丝杠一般有3种旋转梁模型可供选择,即Euler-Bernoulli梁、Rayleigh梁和Timoshenko梁.3种模型均可以用于分析细长梁,但由于Euler-Bernoulli梁和Rayleigh梁忽视了梁横截面的剪切变形,导致它们计算所得梁变形量将低于实际梁变形量,所以采用Timoshenko梁来分析细长梁将获得更好的精确度[3].学者们已经提出了大量动力学模型可深入了解滚珠丝杠传动的振动特性.

付振彪等[4]考虑滚珠丝杠进给系统中各结合面接触刚度的影响,提出了新的有限元建模方法,用于研究滚珠丝杠进给系统的动态特性.钱荣荣等[5]通过有限元分析提出了基于混合基函数的Ritz级数法,分析了滚珠丝杠轴向和扭转的振动特性.Zhang等[6]提出了刚柔耦合振动的综合建模方法,考虑了滚珠丝杠与刚性部件之间的刚柔耦合,并利用Ritz级数法对系统进行离散化,最终对滚珠丝杠在各种工况下的振动特性开展研究,并通过实验验证.Wu等[7]在文献[6]的基础上引入了基于混合基函数的Ritz级数法,研究了丝杠轴向、扭转、横向和弯曲的振动特性,并通过实验验证.肖勇刚等[8]在传统传递矩阵法的基础上,结合龙格-库塔法推导了自由振动下变截面梁的节段和整体传递矩阵,结合边界条件建立了梁自振频率特征方程,运用Wolfram Mathematic编程软件求解其自振频率,确定出前n阶振型.程胜杰等[9]通过Riccati迁移矩阵法对发电机的轴系进行了计算分析,得到了轴系扭转振动的固有频率和振型.Lee等[10]建立了基于经典梁理论的牵引力传递矩阵法,研究了轴向拉伸载荷和移动速度对轴向移动梁在3种不同端部条件下固有频率的影响,通过将预测结果与以往研究结果进行比较,验证了该方法的准确性.Feyzollahzadeh等[11]将传递矩阵法计算过程中“零矩阵”的逆矩阵阶数从2n降到n,使得状态向量和常系数向量的行被改变,传递矩阵由此变为块对角矩阵,这在逆矩阵的计算中更有效,并以旋转梁为例进行了振动分析.Lee[12]建立了精确传递矩阵,分析了旋转惯性对锥形Rayleigh梁自由振动特性的影响,使用Frobenius方法求解微分方程,并制定传递矩阵从起点到终点变换中位移、弯矩和剪切力的状态向量,并与之前研究中预测的结果比较,证明所提方法的准确性.Vicente等[13]和Henke等[14]均采用Ritz法建立了滚珠丝杠进给系统动力学模型,但模型过于简单,并不能完整表述系统的动力学行为.Zhang等[15]利用集中参数法建立了滚珠丝杠进给系统的等效动力学模型,研究了高加速度滚珠丝杠进给系统的动力学特性. Zhang等[16]根据欧拉-伯努利梁理论,利用分段法研究了切削过程中预紧滚珠丝杠的横向振动.

综上所述,虽然传统迁移矩阵法在分析梁单自由度振动问题时,相比有限元法和集中质量法更加简明易懂,但随着科学技术的发展,单自由度的振动问题早已不能满足工程实践的需求.因此,本文利用Timoshenko梁理论对传统迁移矩阵法进行改进,建立系统的耦合振动方程,改善传统迁移矩阵法的不足,为研究梁耦合振动问题提供新思路.

1 理论分析

1.1 建立模型

图1为系统模型及其简化模型.将滚珠丝杠进给系统左、右两端的滚动轴承等效为弹簧,同时将丝杠螺母和工作台等效为安装在丝杠任意位置的负载圆盘.丝杠总长度为L,负载圆盘的集中质量为ms,左端弹簧刚度为K0,右端弹簧刚度为Kn.

图1 系统模型及其简化模型

将滚珠丝杠等效为有限个集中质量,并通过无质量弹性细杆进行连接,负载同样等效为通过无质量刚性细杆连接在圆盘的集中质量,如图2所示.其中,e为圆盘半径,l为划分集中质量后每段弹性杆的长度,mi(i=0,1,2,…,n)为按照设定比例划分后每个集中质量的大小.

图2 滚珠丝杠离散化示意图

1.2 改进迁移矩阵法的应用

取集中质量m0进行受力分析,如图3所示,作用在集中质量m0两侧截面的内力和力矩包括弯矩M、剪力Q和扭矩T.其中,下标为集中质量的序号,上标L和R分别为集中质量左侧和右侧截面处所取值,I为集中质量m0右侧截面和梁l1左端截面的质量惯性矩.假设系统简谐频率为ω,W0和φ0分别为集中质量m0的横向振幅和扭转振幅,则

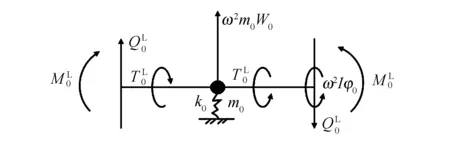
图3 集中质量的受力分析

(1)

根据材料力学可知,ω2m0W0和ω2Iφ0分别为作用在集中质量m0的惯性力和梁l1左端截面的动量矩.同时,根据Timoshenko梁理论可知,造成梁转角的原因是弯矩和剪力.

图4为Timoshenko梁弯曲和剪切变形的叠加[3].左图中剪力Q导致微元产生了剪切角γ0,此时并没有考虑微元转动;而右图中弯矩M导致微元产生了转角φ0,但是并不会改变γ0.因此,集中质量m0的总转角为

图4 Timoshenko梁弯曲和剪切变形的叠加

θ0=φ0-γ0

(2)

同时,因在集中质量m0有

(3)

故θ0=-γ0.根据牛顿第二定律和材料力学可得:

式中:k′为材料的剪切系数,由于滚珠丝杠简化为柔性梁且横截面为圆形,所以k′取0.9;A为横截面的面积;G为材料的剪切弹性模量.

对式(5)两边取微分并将式(4)带入可得:

(6)

由图3可得:

(7)

(8)

式(8)可以表示为

(9)

式中:BS,0为集中质量m0左端状态矢量到右端状态矢量的迁移矩阵,即m0的站迁移矩阵.

同理,效仿集中质量m0的受力分析过程,便可以得到集中质量mn的站迁移矩阵BS,n和其他集中质量的站迁移矩阵BS,i,即

(10)

将安装在滚珠丝杠的负载等效成长度为e的刚性无质量杆和集中质量msi的组合,并将其安装在集中质量mi.滚珠丝杠和负载结合部的受力分析如图5所示.因存在偏心矩e,故一旦此位置发生扭转位移,离心力一定会导致梁产生横扭耦合振动.

根据图5、连续条件和材料力学可得,丝杠负载msi安装在集中质量mi的振幅、扭转角、弯矩和剪力的动力学平衡方程分别为

(11)

(12)

式(12)等号右边的第2项和第3项分别为横向位移和扭转位移导致的惯性力.

再根据式(6)和式(12)可知该位置的转角平衡方程和扭矩平衡方程分别为

(13)

(14)

式(14)等号右边的第2项是切向力导致的转矩,第3项是扭转产生的动量矩.

根据式(11～14)可得集中质量msi左端截面到右端截面的状态迁移矩阵方程为

(15)

式(15)可以表示为

式中:BS,si为集中质量msi左端状态矢量到右端状态矢量的站迁移矩阵.已知集中质量mi与负载msi之间是通过无质量刚性细杆连接的,则当负载位于任意集中质量时,对应站迁移矩阵便为BS,ih=BS,i+BS,si.由此可得:

(16)

在传递矩阵法中,可将无质量弹性杆表述为场.为了将场与站依靠位移、内力和力矩联系起来,取站mi与其两侧的场li和li+1进行受力分析,如图6所示.无质量细杆li的受力分析如图7所示.

图7 无质量细杆li受力分析图

由于细杆无质量,所以剪切力Q对梁转角θ不造成影响,即θ0=φ0.基于图7由平衡条件可得:

(17)

由材料力学可知,图7中细杆li上任意一点的弯矩、转角和挠度可分别表示为

式中:E、J分别为丝杠的弹性模量和横截面对弯曲中性轴的惯性矩.

当式(18～20)中x=xi时,细杆li右端的弯矩、转角和挠度分别为

(21)

根据材料力学可知

(22)

式中:Ip为横截面对扭转中心的极惯性矩.

综上所述,通过式(17～22)可得细杆li左端状态矢量到右端状态矢量的状态迁移矩阵方程为

(23)

式(23)可以表示为

(24)

式中:矩阵BF,i为细杆li左端状态矢量到右端状态矢量的变换矩阵,即li的场迁移矩阵.

根据系统的连续性,式(24)可视为集中质量mi-1右端截面到集中质量mi左端截面状态矢量之间的状态传递方程.将式(24)带入式(16)可得:

(25)

由于只有集中质量mi处施加了集中质量msi,所以除去这部分以外的集中质量与相邻集中质量之间的状态传递方程不再是式(25).以集中质量mi+1为例,通过式(24)可得:

(26)

在式(25～26)中令

(27)

由式(25～27)可得:

(28)

综上可得:

(29)

将式(9)带入式(29)可得:

(30)

式(30)表示从集中质量m0左端截面到集中质量mn右端截面状态矢量之间的状态传递方程.其中,B为整个系统的总迁移矩阵,就是上文所说的6阶迁移矩阵,即

B=BS,nBF,nBn+1…Bi+1·BiiBi-1…B2B1BS,0

2 实验验证

滚珠丝杠进给系统实验平台包括某型号滚珠丝杠进给模组、YMC9216型信号采集器、YMC9800模态分析软件、YMCIH-10PE型激振力锤和YMC121A100型单IEPE加速度传感器,如图8所示.同时,为保证实验数据的准确度,实验坐标系与图1所示的建模坐标系保持一致.表1给出了滚珠丝杠进给模组的基本参数.

图8 滚珠丝杠进给系统实验平台

在实验开始前将负载位置与仿真过程保持一致,均处于丝杠中部.设信号采集器的采样频率为2 000 Hz,刷新频率为1 Hz,采样方式为手动触发,采样时间为4 s.实验开始后,将加速度传感器分别安装在负载表面和伺服电机端部,方向分别沿着y轴正方向和x轴负方向.同时,使用激振力锤分别沿着负载y轴正方向和x轴负方向进行敲击,为了避免实验的偶然性,每组实验需要进行3次敲击.图9为其中1组实验通过YMC9800模态分析软件获得的实验结果.

图9 敲击实验的时域图

对系统y轴和x轴方向实验所获时域信号分别利用Matlab软件进行FFT变换,得到系统y轴和x轴方向频谱曲线对比图,如图10所示.图中,红色实线表示y轴方向频谱曲线,蓝色点划线表示x轴方向频谱曲线.可以看出,2个方向实验结果所对应的共振峰位置基本一致,由此可以确定系统各阶模态下y轴与x轴方向振动必然存在耦合关系.

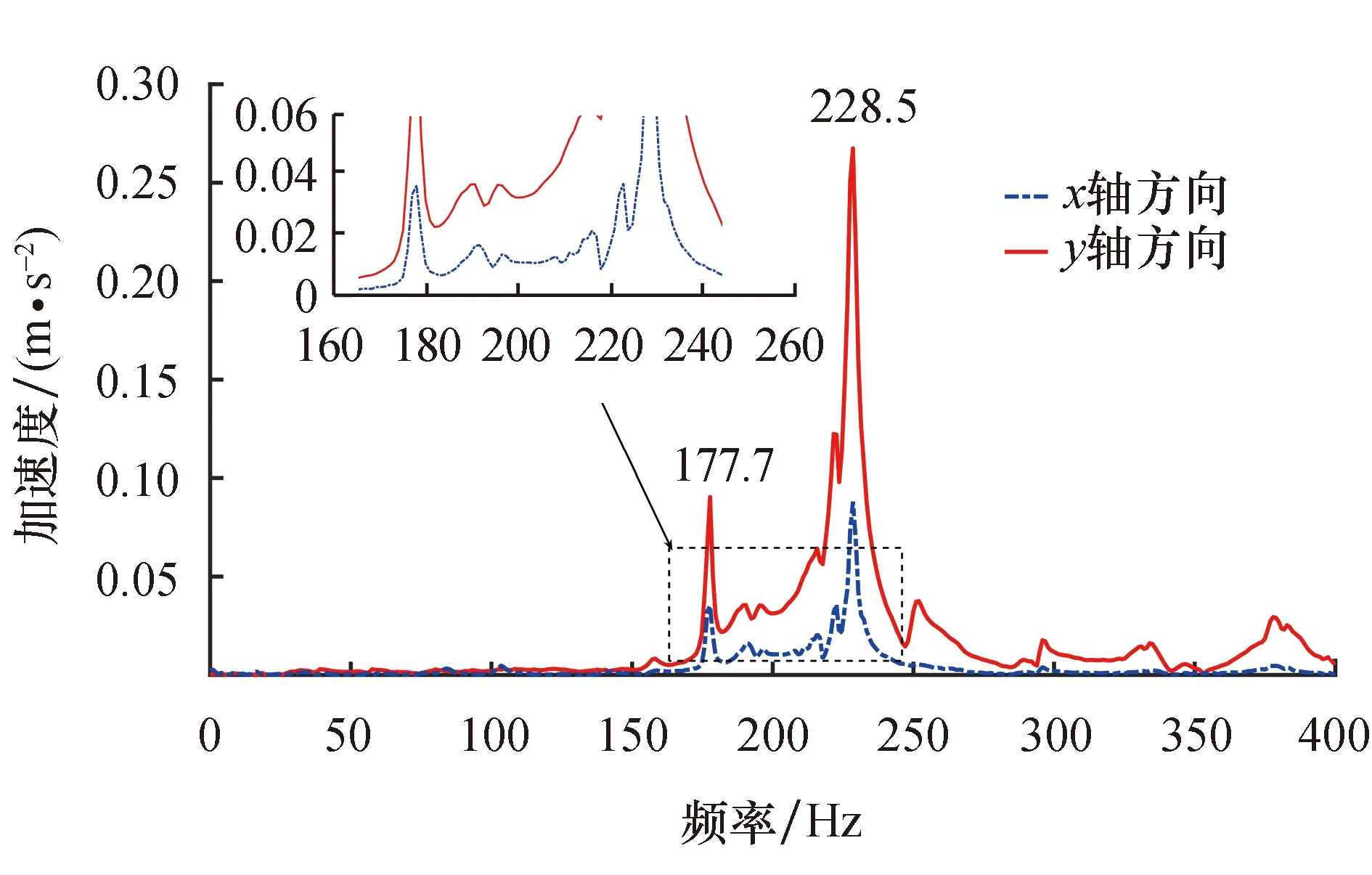
图10 系统y轴和x轴方向振动的频谱曲线

已知滚珠丝杠两端采用滚动轴承支撑,均限制弯曲自由度但不限制转动自由度,则边界条件为

(31)

同时,式(30)的矩阵形式为

(32)

将式(31)带入式(32)可得:

(33)

将式(33)展开为代数方程组,即

(34)

式中:Tmn为总迁移矩阵B中对应位置的元素.

(35)

式(35)是关于固有频率平方的方程,通过求解便可得到系统各阶的固有频率.为了突显改进迁移矩阵法的优势,需要将其与传统迁移矩阵法的固有频率仿真结果进行对比.当使用传统迁移矩阵法[2]进行理论推导时,系统总迁移矩阵中BS,0、BS,n、Bii和Bj(j=1,2,…,n+1)分别为

同时,式(35)变换为

(36)

通过式(35)和式(36)分别得到2种方法求解后系统的前2阶固有频率,表2为图10的实验结果和2种方法的仿真结果.通过对比可以看出:传统的迁移矩阵法确实无法分析多自由度刚柔耦合系统的固有频率,仿真结果与实验结果误差过大;反之,改进迁移矩阵法得到的固有频率能够较好地拟合实验结果.然而,本文建模过程的简化和实验过程的环境因素导致仿真结果与实验结果存在一定误差.

表2 系统前2阶固有频率的仿真和实验结果

3 振动特性研究

根据式(34)可得:

(37)

记

(38)

取集中质量个数为40,负载质量保持不变的同时,图11给出了负载处于0.20L、0.35L、0.75L和0.90L时滚珠丝杠前2阶的模态振型.可以看出:滚珠丝杠前2阶的横向振动与扭转振动之间必然存在着某种耦合关系,且横向振动占据着主导地位;随着负载位置不断变化,滚珠丝杠的模态振型主要呈现出振幅和振型节点的变化,原因是负载位置直接影响着滚珠丝杠的整体受载情况,进而影响着丝杠的结构刚度.同时,滚珠丝杠第2阶模态振型相比第1阶更加复杂,且受负载位置的影响更大,从而第2阶模态下滚珠丝杠的横扭耦合关系更加复杂.

图11 负载位置不同时滚珠丝杠的横向和扭转振型

图12为负载与系统固有频率的关系示意图,同样取集中质量个数为40,令负载位置和质量分别处于0.20L～0.80L和0.30ms～0.96ms.可以看出:第1阶模态固有频率主要受到负载质量的影响,在丝杠中部刚度最小的部位显而易见,随着负载质量增加,固有频率迅速减小;第2阶模态固有频率主要受到负载位置的影响,当负载位于丝杠中部时固有频率最小,负载位置越靠近丝杠两端频率越大,随着负载质量增加,频率轻微地减小.

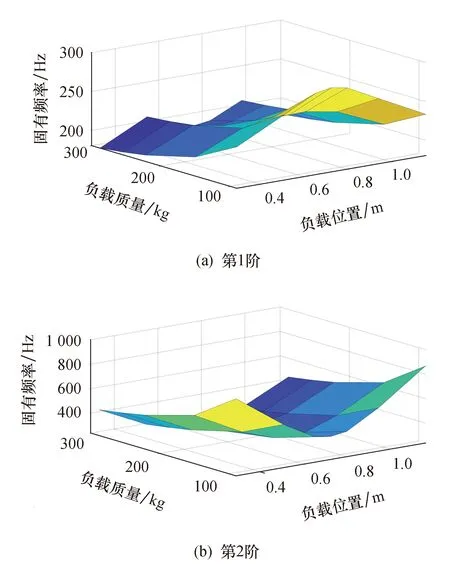
图12 负载与系统固有频率的关系示意图

4 结论

通过实验结果可知,本文所提改进迁移矩阵法在系统前2阶固有频率的数值仿真计算中相比传统迁移矩阵法精度分别提高了62.0%和412.8%.由此说明,改进迁移矩阵法能够更加有效地解决传统迁移矩阵法不能解决的多自由度耦合振动问题.

通过对系统振动特性的研究可以发现:滚珠丝杠横向振动与扭转振动之间确定存在着一定的耦合关系,且随着系统模态阶数的增大耦合关系更加复杂;同时,随着系统模态阶数提高,负载质量大小和位置变化对系统固有频率的影响逐渐增强.对于多自由度梁类系统更加复杂的耦合振动研究,此结论可以提供一定的理论帮助.