立足学生经验的高中数学概念教学实践与思考

戴鼎君

［摘 要］概念教学是高中数学教学的根基，是落实数学学科核心素养的关键。在概念教学中教师应关注学生已有的经验，引导学生积极参与学习与探究，助推学生的经验生长。文章以“数列的概念”教学为例，从生活经验、知识经验、方法经验三个方面探讨立足学生经验的高中数学概念教学。

［关键词］概念教学；学生经验；数列

［中图分类号］    G633.6        ［文献标识码］    A        ［文章编号］    1674-6058（2023）17-0006-03

数学概念是反映现实世界的空间形式和数量关系的本质属性的思维形式。数学概念教学的重要性不言而喻。在高中数学概念教学中，部分教师轻概念、重解题，将大量的时间放在引导学生解题上，认为通过解题训练，可使学生深入理解概念，致使学生对概念的本质一知半解，也无法利用概念来解决问题。

在高中概念教学中，教师应引导学生体会概念的生成过程，帮助学生把握概念的本质，领悟思想方法。学生经验是教育的起点，有效的教学应该关注学生的经验，助推学生的经验生长。下面笔者以“数列的概念”教学为例，探讨立足学生经验的高中数学概念教学。

一、教学过程

（一）立足生活经验，初步认识数列

师：同学们，老师想了解一下你们的数学学习情况，于是在智学网上查阅了你们近5次的周测成绩，以下是甲、乙两位同学的成绩，你们能帮老师分析一下他们最近的学习情况吗？

［案例1］甲的成绩：80，82，86，90，95；乙的成绩：90，87，92，83，87。

生：甲同学一直在进步，说明他学习很认真；乙同学成绩有波动，说明他专注力不够集中。

师：分析得非常准确！若老师将两位同学的成绩按从小到大的顺序发送给他们的父母，你们觉得合适吗？

生：甲同学可以，乙同学不行。

师：为什么呢？

生：甲同学的成绩是从小到大排列的，这样发送没有破坏顺序；而乙同学的成绩本身不是从小到大排列的，这样发送会破坏原本的顺序，无法体现出成绩的变化情况。

师：这说明了什么？

生：说明成绩应该保持其原本的顺序，不可随意调换顺序。

师：也就是说成绩是具有确定顺序的一列数。生活中这样的例子还有很多，你能列举出来吗？

（学生列举身高、体重、温度等例子）

师：同学们举的例子都非常好，老师再给大家提供两个例子。

［案例2］王芳1歲到17岁生日当天的身高数据：75，87，96，103，110，116，120，128，138，145，153，158，160，162，163，165，168。

师：你能归纳出以上3个例子的共同特征吗？

生：都是按照确定的顺序排列的一列数。

师：同学们归纳得非常准确，我们把按照确定的顺序排列的一列数称为数列。

（二）立足知识经验，深刻理解数列

师：83，87，87，90，92是数列吗？

生：是的，它是按照从小到大的顺序排列的。

师：它与90，87，92，83，87是同一数列吗？

生：不是，它们的顺序不同。

师：很好！讲到顺序，你们会联想到之前学过的哪个知识点？它们有何区别？

生：集合。集合中的元素是不讲顺序的。

师：非常好，你们记得很清楚。83，87，87，90，92中有两个87，能将其中一个去掉吗？

生：不可以，若去掉，它们的顺序就会发生改变，就不是原来的那个数列了。

师：这说明了什么呢？

生：说明数列中的数是可重复的。

师：这也是数列和集合的另一个区别。既然数列是有顺序的，那么我们在说的时候就要强调它的顺序，比如数列中的“第1个数”“第2个数”……数列中的每一个数叫作数列中的项，第1个数称为“第1项”或“首项”，第2个数称为“第2项”，以此类推。数列的一般形式可以写成[a1]，[a2]，[a3]，…，[an]，简记为[an] （强调[an与an] 的区别）。

师：你们还记得是如何给集合分类的吗？

生：根据元素的个数进行分类，元素个数有限称为有限集，元素个数无限则称为无限集。

师：类比集合的分类，我们可将项数有限的数列称为有穷数列，项数无限的数列称为无穷数列。

（三）立足方法经验，自主探究数列

［练习1］案例3中的数列的[a1]、[a2]、[a5]项各是多少？

生：可以得出这个数列的所有项。

师：这是一个无穷数列，你能算出它的所有项吗？是把它们都算出来吗？

生：不是，无穷数列是无法写完的，可由这个式子得到数列中的任意一项。

师：这个说法比较准确，可以由这个式子得到数列中的任意一项，比如说第10项、第20项、第30项等。我们可令[n=1]、2、3、4…，将它们代入[an]中，这样就能“对应”得到[a1]、[a2]、[a3]、[a4…]。提到“对应”，你们会联想到之前学过的哪个知识点呢？

生：函数。

生：是函数。

师：你是如何判断的？

教师：可结合函数的定义来判断（定义域中的每一个[x]都有唯一的[y]与之对应）。

师：请观察案例1与案例2中的数列，并思考是否所有数列都是函数。

生：所有数列均为函数。

师：数列本质上是从正整数集[N∗] （或它的有限子集[1，2，…，n]）到实数集R的函数，自变量为项的序号[n]，对应的函数值为数列中的第[n]项[an]。

师：类比是高中数学学习的重要方法，既然数列是函数，那我们可以从哪些角度来研究数列呢？

（2）列表法

（3）图象法

师：用列表法也可以表示数列。与函数类似，列表法明确地列出了数列中的每一项，而且表示出了序号与项的对应关系。

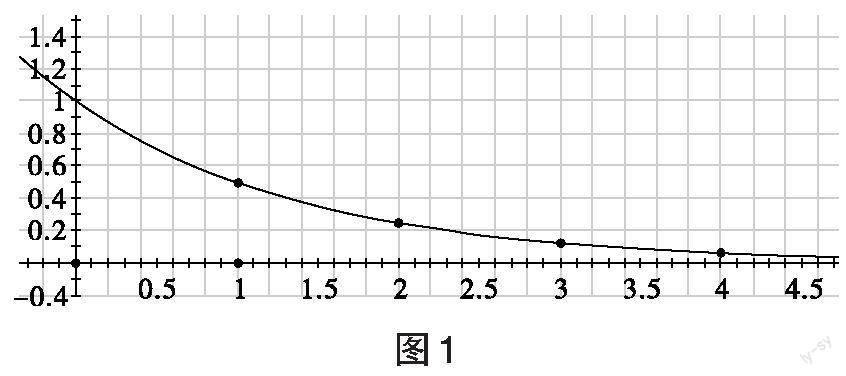
师：这位同学画的图象（见图1）正确吗？

生：不正确，图象应该是一些点，不能用线把它们连起来。

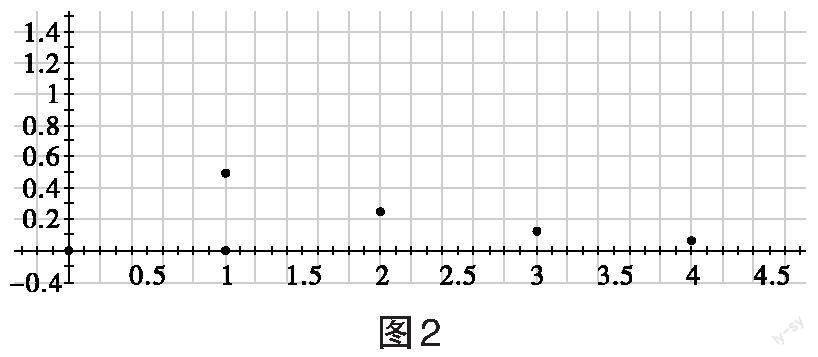
师：不错，由于数列的定义域是[N∗] （或它的有限子集为[1，2，…，n]），所以不能用线将点连起来，即数列的图象应该是一些离散的点，正确的图象如图2所示。

师：通过观察图象，你认为数列具有哪些性质？

生：数列具有单调性。

生：通过图象可以看出该数列呈现单调递减的趋势，案例2中的数列呈现单调递增的趋势，说明数列具有单调性。

师：非常棒！当然也不是所有数列都具有单调性（如案例1中乙同学的成绩），依据单调性，我们可以将数列分为单调递增数列、单调递减数列、常数列、摆动数列（有增有减）。

师：那数列具有奇偶性吗？

生：由于数列的定义域不关于原点对称，因此数列不具有奇偶性。

师：很好！根据函数奇偶性的定义，数列也不具有奇偶性。

生：第1个数列的通项公式写不出。

师：的确，第1个数列的通项公式无法写出，与函數不一定存在解析式相类似，数列也不一定存在通项公式。

生：第2个数列的通项公式是[an=2n]，[n∈N∗]。

生：无法表示出一正一负交替出现。

师：正确。还有其他表示方法吗？

师：可将数列中的每一项写成：1+1，1-1，1+1，1-1，1+1，1-1，…，那么也可以写成[an=1+（-1）n+1]，[n∈N∗]，这说明了什么？

生：同一个数列可能存在不同的通项公式。

师：很好，同一个数列的通项公式不唯一。

师：通过2，0，2，0，2，0，…这个数列，你还能发现数列具有什么性质？

生：这是一个周期为2的数列。

师：太棒了！数列也具有周期性。

师：请同学们回顾一下本节课我们学到了什么？

（学生自主归纳本节课学到的知识及思想方法。）

师：结合刚刚探究数列的过程，你能猜想一下我们之后的课程要学习什么新内容吗？

生：特殊的数列。

二、经验总结与思考

（一）准确把握学生经验

在进行概念教学时，教师要充分考虑学生的已有经验并思考如何立足学生的经验开展教学，如何通过教学使学生的经验获得“生长”。教师立足学生的经验进行教学预设，有利于准确把握教学起点，灵活调整教学方案，帮助学生理解新知、巩固旧知。

（二）精准理解学生经验类型

学生的经验有很多，但有的经验是错误的，有的经验虽然正确但不完善，而有的经验学生无法迁移运用。对于学生的不同经验，教师要精准理解并利用不同的策略进行应用。错误的经验会抑制学生的学习，因此教师可通过创设情境或提出问题，引发学生的认知冲突，引导学生反思错误经验，纠正错误认识。对于学生正确但不完善的经验，教师可通过问题链的形式引领学生拓展深化，逐步完善。对于学生无法迁移的经验，教师要找准迁移点，将新知与已有经验进行对比、联系，促进学生的经验“生长”。

（三）充分发挥学生经验作用

教师在概念教学中要充分发挥学生经验的作用，创设与学生生活经验有关的情境，激发学生的学习兴趣，使新概念在与生活的联系中自然生成，使学生易于接受与理解。在新知生成之后，教师可联系学生已有的知识经验，将新知与旧知进行比较，找到它们的区别与联系，使学生更准确、更深刻地理解新知，并将新知纳入已有的知识体系中。在学生充分理解新知之后，教师可结合学生已有的方法经验，引导学生自主探究新概念的相关性质与特征，培养学生的自主探究意识和能力，提升学生的数学思维能力。

综上，数学概念是数学学科的根基，也是学生学习的难点。概念教学不是一蹴而就的，是一个循序渐进、连续发展的过程。立足学生经验的概念教学，应在学生学习新知的基础上，引导学生不断地对已有的知识、经验与方法进行回顾、总结，巩固旧知、探索新知，构建完整的知识体系，培养数学学科素养。

［   参   考   文   献   ］

［1］  蔡海涛，林运来.核心素养下高中数学概念课教学策略［J］.数学通报，2019（9）：20-25，66.

［2］  中华人民共和国教育部.普通高中数学课程标准：2017年版2020年修订［M］.北京：人民教育出版社，2020.

［3］  杜威.我们怎样思维·经验与教育［M］.姜文闵，译.北京：人民教育出版社，2005.