平面向量综合问题分类导析

陈元菊

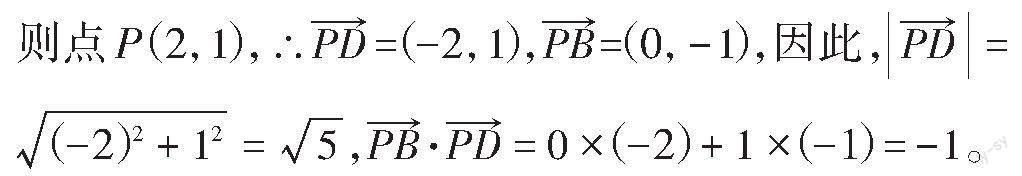
［摘 要］平面向量是高中数学的重要概念与工具。平面向量融数、形于一体，具有代数与几何的双重身份。平面向量既体现“形”的直观特征，又体现“数”的运算特征，因而平面向量是联系几何图形和代数运算的纽带，平面向量还是数学学科知识交汇和联系多项内容的媒介。平面向量与代数、几何以及三角都有着千丝万缕的联系，是高中数学众多知识网络中的交汇点。平面向量的引入，能大大拓宽学生解决数学问题的思路，为高考试题的命制提供了一个相对丰富的脉络。在高考中，平面向量常与解三角形、三角函数、平面几何、解析几何等知识进行综合考查。鉴于平面向量的重要作用，文章重点分类探析平面向量综合问题，以期帮助数学教师了解平面向量在高考中题型的变化和发展趋势。

［关键词］平面向量；综合问题；解三角形；三角函数；平面几何；解析几何

［中图分类号］    G633.6        ［文献标识码］    A        ［文章编号］    1674-6058（2023）17-0017-04

高中數学知识纵横联系、互相渗透。高考数学试题突出考查知识的全面性和综合性，强调知识的交汇和融合，试题往往设计在知识网络的交汇处，特别注重考查学生解决问题的能力。平面向量融数、形于一体，具有代数和几何的双重身份，是一种沟通代数、几何与三角的重要工具。下面笔者以例题解析的形式，分别探讨平面向量与其他知识的综合，以期帮助数学一线教师了解平面向量在高考中题型的变化和发展趋势。

一、平面向量与解三角形的综合

平面向量与解三角形的综合体现在：平面向量的几何意义与三角形几何特征的联结，三角形的边长向量描述为向量的模，三角形内角（或内角的补角）的向量描述为向量的夹角，平面向量的加法、减法、数量积运算可沟通三角形边、角运算，正弦定理、余弦定理、三角形面积公式也都和平面向量运算有着直接或间接的联系。

平面向量与解三角形的综合知识：

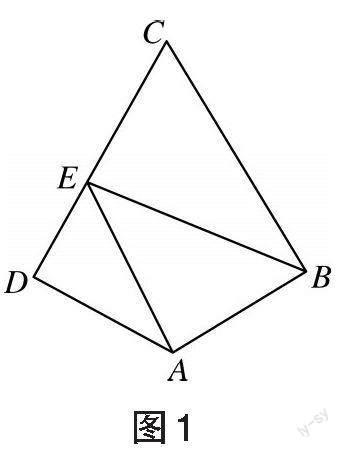
在[△ABC]中，内角[A、B、C]所对的边分别为[a、b、c]，[D]是边[BC]的中点，则有：

∴[2·BC·（-cosB）=1]，∴[2·BC·cosB=-1] （1）

由三角形的余弦定理可得

[AC2=AB2+BC2-2AB·BC·cosB]

∴[32=22+BC2-4·BC·cosB]  （2）

点评：在这个问题中平面向量数量积运算发挥了牵线搭桥的作用，利用平面向量数量积运算建立起了三角形的边长与内角之间的数量关系，把问题由向量计算转化为三角形的边长与内角计算。此题余弦定理的应用也很关键，进一步沟通了三角形边和内角的数量关系，在求解过程中运用了方程思想。

点评：此题对学生思维能力的考查力度大，用常规方法去解题无从下手。由点[D]是边[AC]的中点联想到三角形中线向量的性质，向量的平方等于向量模的平方，而向量的模即是三角形中有关线段的长度。此题解题过程中平面向量的切入，起到了“一点突破，全线贯通”的作用，特别是在计算过程中，平面向量数量积贯通了三角形的边、角的关系。平面向量运算与三角形边、角运算高度契合，可以体会到平面向量与解三角形的综合，给了这样的问题一个创新思路。

平面向量与解三角形的综合规律总结：

1.以平面向量为载体，交叉综合解三角形；

2.以三角形为载体，利用平面向量数量积和模的概念等脱去平面向量的“外衣”，转化为三角形的边、角问题。

二、平面向量与三角函数的综合

平面向量与三角函数的综合也是高考的重点和热点，平面向量与三角函数综合问题一般是以三角函数为背景，根据平面向量的加法、减法、数乘向量、数量积等运算性质，将平面向量问题转化为三角函数的相关问题来解答。此类问题往往融合向量的数量积、向量的模 、向量的坐标表示以及三角函数的性质、公式、化简、最值，具有覆盖面广、综合性强、解法灵活的特点。

平面向量与三角函数的综合常涉及向量的坐标运算：

点评：此类问题中平面向量本质上只是作为知识背景或载体的形式出现，考查重点实际为三角函数，解题的关键是恰当地实施三角函数知识与平面向量知识的转化。

平面向量与三角函数的综合规律总结：

题目条件给出平面向量的坐标中包含有三角函数的形式，一般通过平面向量平行、垂直、向量模、数量积的运算，将平面向量转化为三角函数中的数量关系，然后再结合三角函数的图象与性质进行求解。

三、平面向量与平面几何的综合

平面向量与平面几何的综合问题的解题关键是：根据平面向量在平面图形中的几何意义，将平面几何的问题化归为平面向量的问题来处理，或者将平面向量的问题化归为平面几何的问题来处理。

平面向量与平面几何的综合知识：

点评：结合平面向量共线定理，把几何问题中三点共线转换成向量共线，参数[t]的引入，把平面向量数量积转化为关于[t]的函数，利用函数性质可求得最小值。

点评：解决涉及平面几何图形的向量运算问题常有两种方法：一是定义法，二是坐标法。定义法即根据平面向量的几何性质，建立起平面几何与平面向量的关系，用平面向量表示问题中的有关几何元素，如平面向量的三角形加法法则、平行四边形加法法则、三角形减法法则、数量积的定义，将平面几何问题转化为平面向量问题。坐标法即把平面几何图形构造到平面直角坐标系中，赋予图形中有关点的坐标、有关平面向量的坐标，一旦引入向量的坐标表示，向量的加减、向量的模、向量的数量积等运算，就都可以转化为代数运算，这样就可以将形与数紧密结合在一起。对于长方形、正方形、直角三角形中的向量运算，可以考虑建立直角坐标系，用平面向量的坐标法解决，把几何关系“翻译”成向量坐标运算，这样可以大大优化解题过程。

平面向量与平面几何的综合规律总结：

平面向量与平面几何的综合问题考查平面几何问题中向量知识的运用，常以平面几何的基本图形（如三角形、四邊形等）为背景，从平面向量的“数”和“形”两个方面特征入手进行思考。如果重点考查平面向量的“数”的特点，就要从平面向量的代数运算上去突破，可以建立适当的平面直角坐标系，设点坐标，进而求出平面向量的坐标，再进行向量运算，把问题转化为代数问题。如果重点考查平面向量的“形”的特点，就要从平面向量的几何意义上去突破，这就需要选择两个合适的向量作基底，根据平面向量的几何意义，将问题转化为平面几何中“形”的问题。

四、平面向量与解析几何的综合

从“形”的角度看，平面向量是有方向的线段；从“数”的角度看，平面向量的坐标可以用它的起点和终点的坐标来表示；在思想方法上，平面向量和解析几何保持高度一致，所以平面向量和解析几何有着天然的内在联系。平面向量的形式和语言经常出现在解析几何问题中，涉及平行（共线）、垂直、夹角、长度、轨迹等问题的处理，解决问题的基本思路有两种：一是利用平面向量坐标表示，把几何推理、证明转化为代数运算，即把“形”转化为“数”；二是将平面向量代数运算转化为平面图形的位置关系，即把“数”转化为“形”。

平面向量与解析几何的综合：

1.以平面向量为载体，在平面向量与解析几何知识层面上进行整合，几何元素之间的平行、垂直、共线等关系运用平面向量的语言来描述和解析，综合考查学生对平面向量的加法、减法，平面向量的数量积运算及其几何意义，以及对圆锥曲线的定义和性质的理解。

2.以平面向量作为工具，在平面向量与解析几何应用层面上进行整合，考查学生对平面向量的概念、加减运算几何意义、坐标表示、数量积几何意义、平面向量共线定理的理解。另外，圆锥曲线的标准方程及有关角度、长度、轨迹等问题，都可应用平面向量数量积的运算来解决。

A. 外心 B. 内心 C. 重心 D. 垂心

解析：∵抛物线的解析式为[x2=-8y]，准线为[y=2]，∴[A（0，2）]，

设[MN]的中点为[P]，由向量加法法则得

∴[PB]垂直平分线段[MN]。

设直线[MN]的方程为[y=kx+2]，与[x2=-8y] 联立消去[y]，得[x2+8kx+16=0]，由[Δ>0⇒64k2-4×16>0⇒k2>1]，

点评：处理解析几何中的垂直问题，可根据平面向量垂直的充要条件[a·b=0⇔a⊥b]（[a、b]是非零向量）。

平面向量与解析几何的综合规律总结：

1.解析几何中复杂的推理、位置关系可根据平面向量的几何意义，运用坐标进行转化，通过向量坐标演化成简单的代数运算，转化途径主要有两种：一是利用平面向量数量积的公式和性质；二是利用平面向量平行或垂直的充要条件。

2.某些解析几何问题若用常规方法去解决，会因为运算繁杂而导致失败，不妨利用平面向量作形与数的转化，即把平面向量作为工具去探索圆锥曲线的标准方程和几何性质，回归到解析几何的基本思想方法，这样会大大简化解题过程。

综上可知，平面向量与解三角形、三角函数、平面几何、解析几何的综合，凸显了平面向量的交汇性和工具性。平面向量与代数、几何、三角都具有相当高的融合性，平面向量使整个高中数学教材体系更富有活力，平面向量为学生解决问题提供了一种有效捷径。用平面向量作为工具处理有关问题，简练优美，极具优越性。教师应引导学生理解平面向量的两个核心特征：几何特征和代数特征，把握平面向量与其他知识的内在联系，进行平面向量与其他知识间的综合，树立应用平面向量解决问题的意识。

［   参   考   文   献   ］

［1］  余华安.例谈平面向量在解析几何问题中的应用［J］.中小学数学（高中版），2008（Z1）：64-66.

［2］  王红革，许志勇，沈婕.高考中“平面向量”测试对教学的反拨效应分析：以普通高考（天津卷）为例［J］.考试研究，2014（2）：3-9.

［3］  干亚清.平面向量在解析几何中的应用［J］.高中数学教与学，2011（14）：46-47，40.

［4］  伊建军.平面向量题型与高考走势［J］.中学教研（数学），2008（2）：26-28.

［5］  陈利民.平面向量及其运用［J］.中学教研（数学），2013（2）：1-4.