求轨迹方程方法研究

许莉

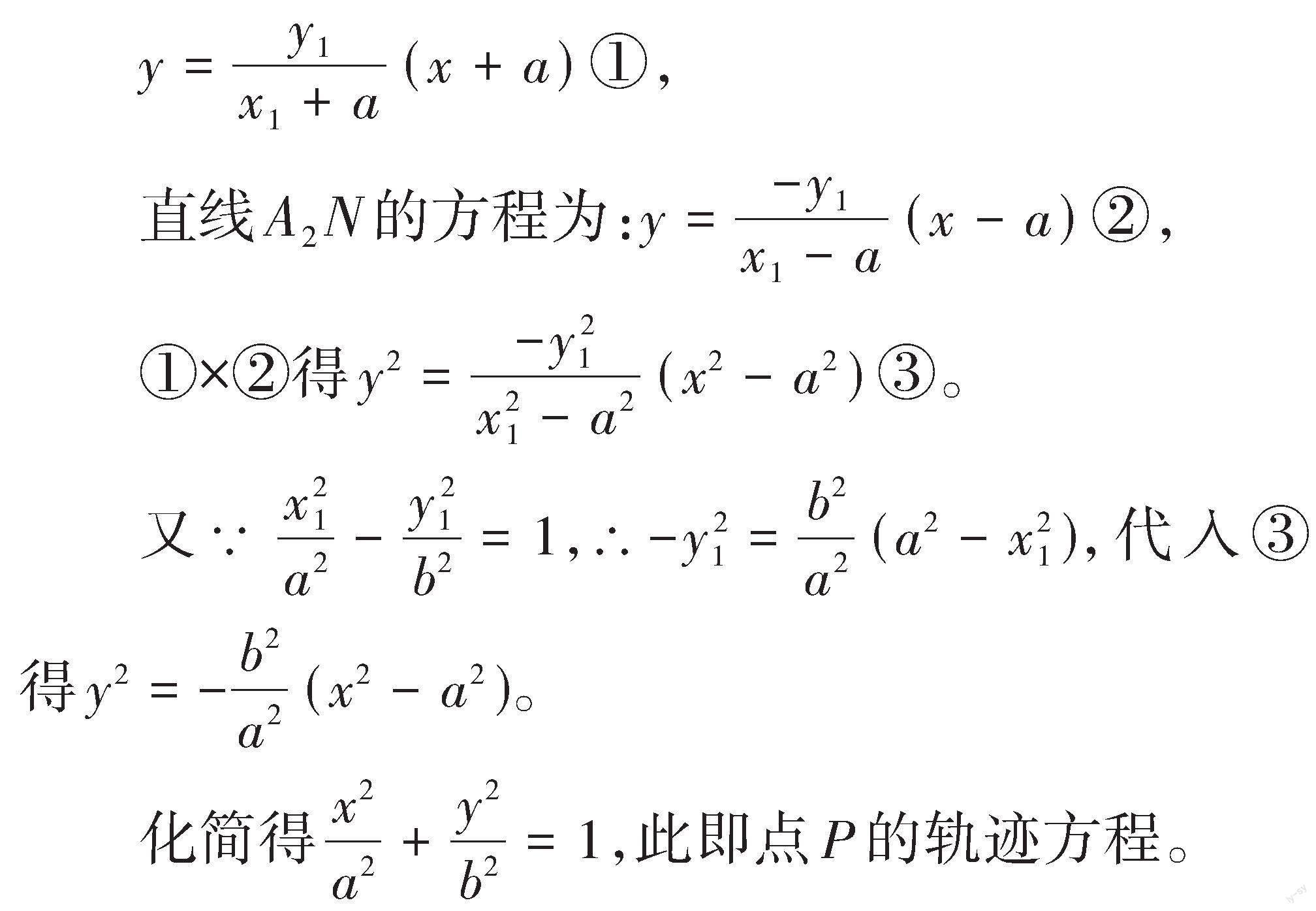
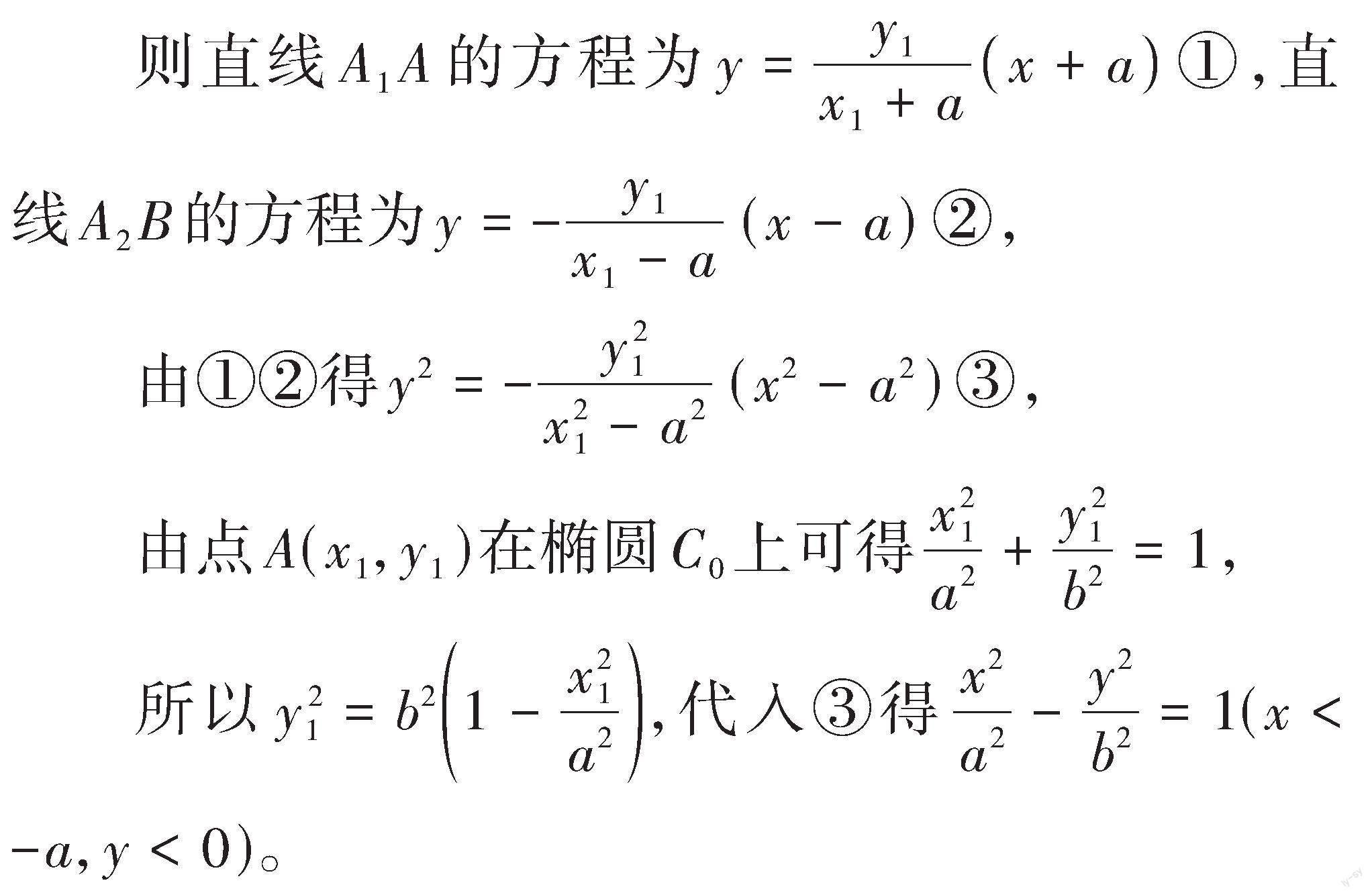
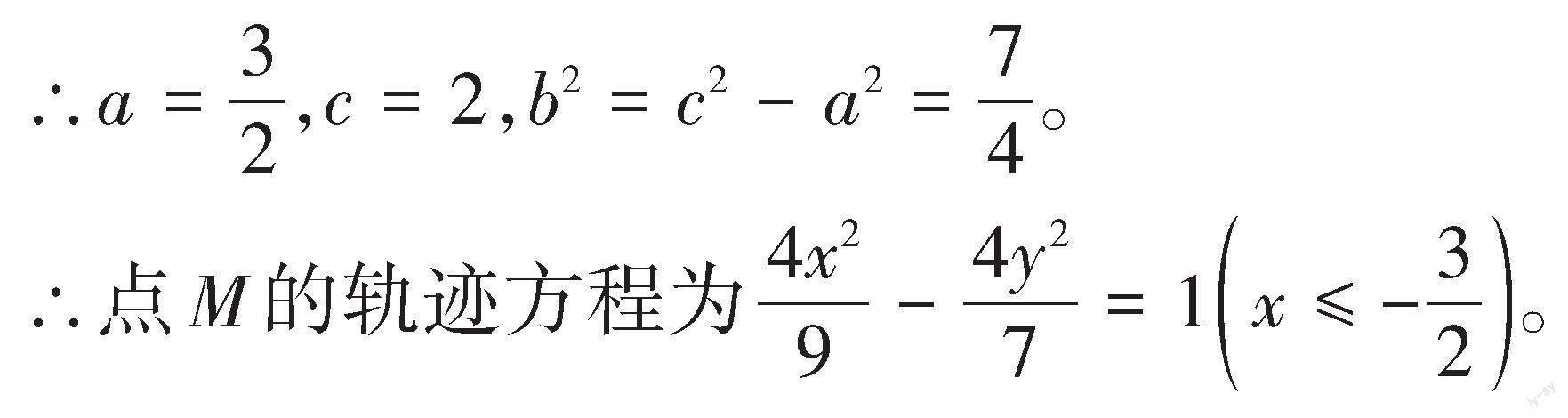
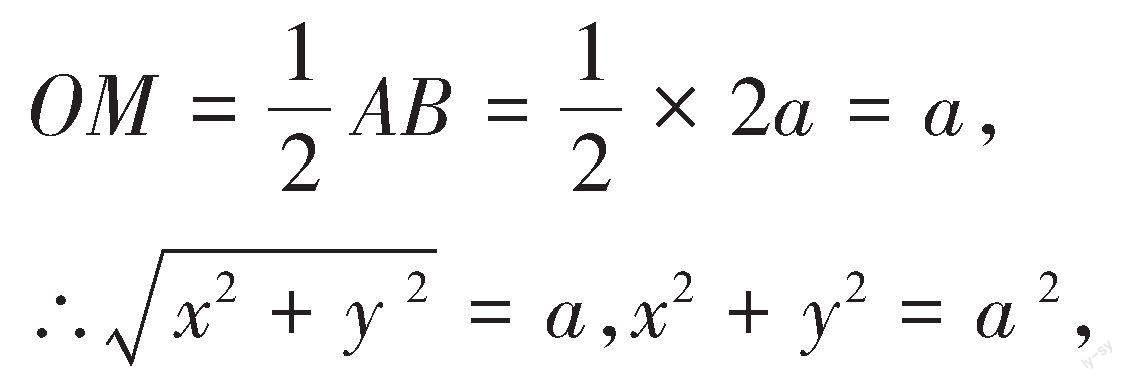
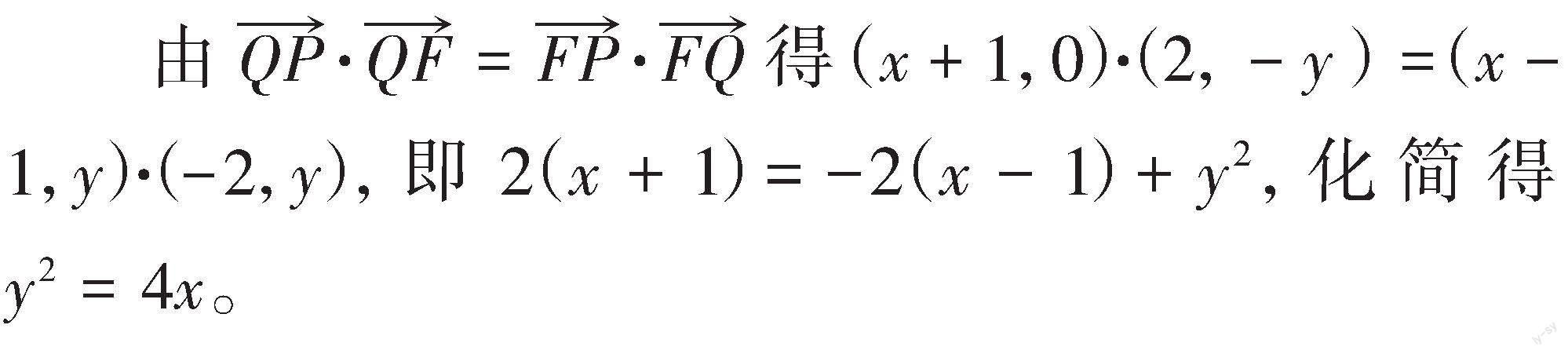
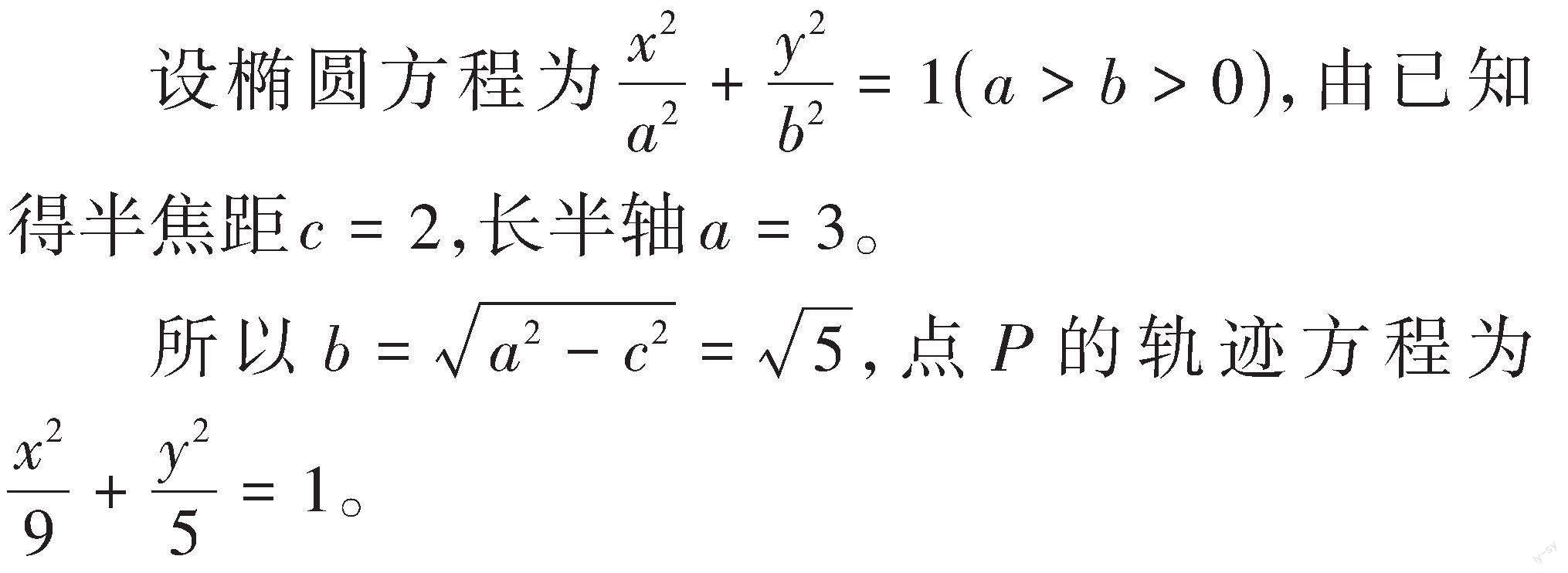
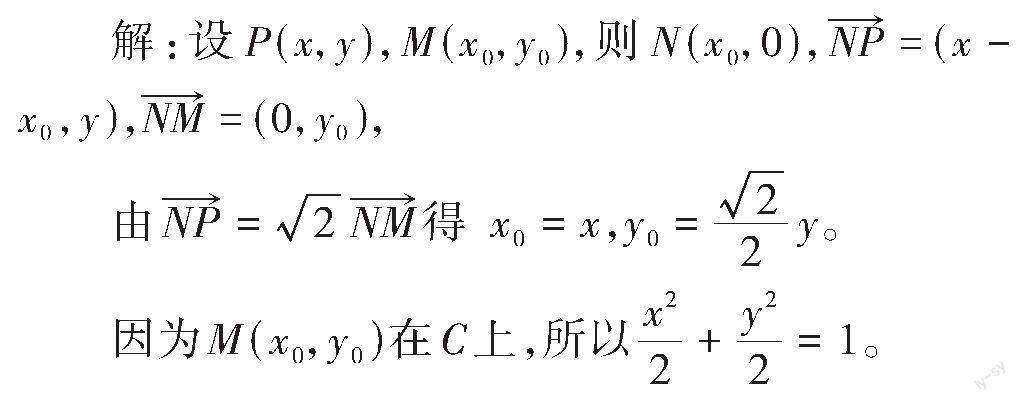
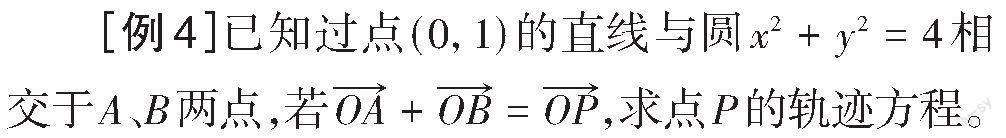
［摘 要］求轨迹方程是高中数学解析几何常见的一类题型，由于动点运动规律给出的条件差别很大，很多学生找不出条件之间的联系。文章总结了直接法、定义法、相关点法、参数法、交轨法、齐次化法等常用的解题方法，并配以相应的数学例题，对这些方法进行了归纳整理，以提高学生的解题能力。

［关键词］轨迹方程；方法；交轨法

［中图分类号］    G633.6        ［文献标识码］    A        ［文章编号］    1674-6058（2023）17-0013-05

求轨迹方程是解析几何的重要内容，也是高考中常考的题型，很多学生在处理这类题目时会感到有些困难，因为不懂得寻找题干的内在规律和知识之间的相互联系，建立了坐标系后，尽管进行了大量的数学运算，仍然没有办法得到正确的轨迹方程。其实，求轨迹方程的方法是多种多样的，只要能够准确审题，并运用正确的方法，问题自然就迎刃而解了。

首先，要了解“动点轨迹”的概念。我们把平面上具有某种共同属性的动点的集合，叫作该动点的轨迹。动点的轨迹可以是平面上的点集，也可能是一些孤立的点，一般情况下是曲线或曲线段，高中阶段主要研究直线或线段或圆锥截线段等。

其次，对“曲线”“方程”概念的了解。若曲线 [C ]与某一双变量方程[f（x，y）=0]有下列对应性关系：满足方程的都是曲线上各点的坐标。 如果通过解方程，所得的解都在同一条曲线上，这个方程就可以叫作曲线的方程。反之，给出曲线，就可以找到对应的方程，这个方程就可以叫作曲线的方程。

再次，求动点轨迹方程的一般步骤为：

（1）建（建立合适的坐标系）；

（2）设（设轨迹上的动点为[P（x，y）]）；

（3）列（列出动点所满足的条件式）；

（4）代（根据条件特点，选择等式，如距离、斜率等变换）；

（5）化（化简所得的方程）。

最后，求动点轨迹方程的基本方法是借助直角坐标系，使几何的点集与代数的方程对应起来。因此它的实质是形数对应、形数结合与转化的思想方法。求轨迹方程的方法比较多，下面介绍常用的几种方法。

一、直接法

如果动点运动的条件是一些几何量的等量关系，处理这些条件就不需要特别的技巧，直接列出符合出动点的等量关系式，这样就可以直接得出轨迹方程，这种方法称为直接法。

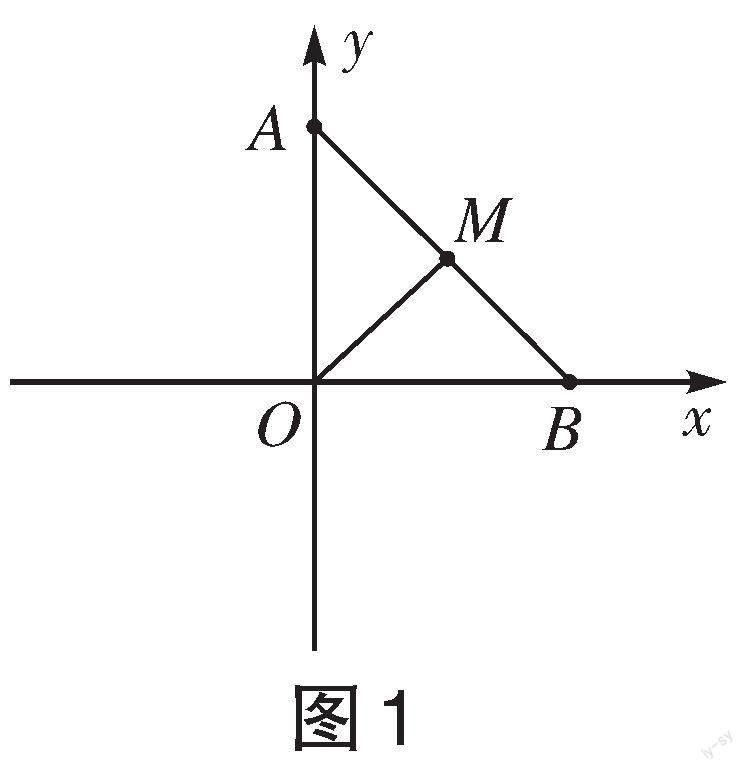
［例1］若线段AB的长度是一个定值[2a]，线段的两个端点[A]和[B]分别在[y]轴和[x]轴上滑动，求[AB]中点[M]的轨迹方程。

分析：题目没有给坐标系，需要建立适当的坐

解： 设[M]点的坐标为[（x，y）]，在直角三角形[AOB]中，由中线定理得

所以[M]点的轨迹是以[O]为圆心，[a]为半径的圆。

直接法有下列几种情况：

（1）如果题目中包含了已知等量关系，求动点的轨迹，可以直接用代数法表示，那么这些量关系就直接用代数法代入计算。

（2）题目未给出坐标系时，需要根据题目设定的条件，选择合适的坐标系，列出符合条件的等式，这样便可求得该图形的轨迹方程。

（3）有时要使用符合题设的相关公式，使其式子中含有动点坐标，进行相应的恒等变换。

（4）有时动点规律的数量关系不明显，它们之间的数量关系可以利用勾股定理、垂线定理、中线定理、连心线等平面几何中的定理、性质进行分析。

分析：本题给出的条件已经可以直接找出点[P]所满足的式子，故而可以直接写出点[P]满足的方程，从而得到曲线[C]的方程。

解：设点[P（x，y）]，则[Q（-1，y）]，且[F（1，0）]。

故动点[P]的轨迹[C]的方程为[y2=4x]。

点评：虽然题目条件很难判断动点[P]的运动规律是否符合某些曲线的定义，但题目中的条件有明显的等量关系，用向量推导出来，就能得到轨迹方程。因此，直接法在求轨迹方程的题目当中的应用是很广泛的，需要引起学生的重视。在计算轨迹方程时，要求尽量简单化，虽然这样有时会使方程的同解性遭到破坏，但是可以通过画图检验，把漏点加进去，或者把多余的点删掉。

二、定义法

如果动点 [P] 的运动规律符合我们已知的某种曲线的定义（如圆、椭圆、双曲线、抛物线），可以先设出轨迹方程，然后在方程中根据已知的条件求出常数，就可以得到轨迹方程。

［例2］如图3所示，[M（-2，0）]和[N（2，0）]是平面上的两点，动点[P]满足：[PM+PN=6]，求点[P]的轨迹方程。

分析：由已知，可根据椭圆的定义，判断点[P]的轨迹为椭圆，设出椭圆方程，利用待定系数法，分别求解出[a、b]即可。

解：由已知，[M（-2，0）]和[N（2，0）]是平面上的兩点，动点[P]满足[PM+PN=6>MN=4]，

由椭圆的定义可知，点[P]的轨迹是以[M（-2，0）]和[N（2，0）]为焦点，长轴为[6]的椭圆。

点评：求轨迹方程时，如果相关问题与圆锥曲线有关，要注意观察动点 [P] 的轨迹与圆锥曲线的定义是否一致。如果符合我们熟悉的某条曲线的定义，那么可以先根据已知的情况确定轨迹方程，然后进行计算，这样轨迹的方程就可以得到了。同时，一定要注意所求的轨迹是完整的圆还是完整的椭圆、双曲线、抛物线等，如果不是完整的曲线，就需要限定取值的范围。

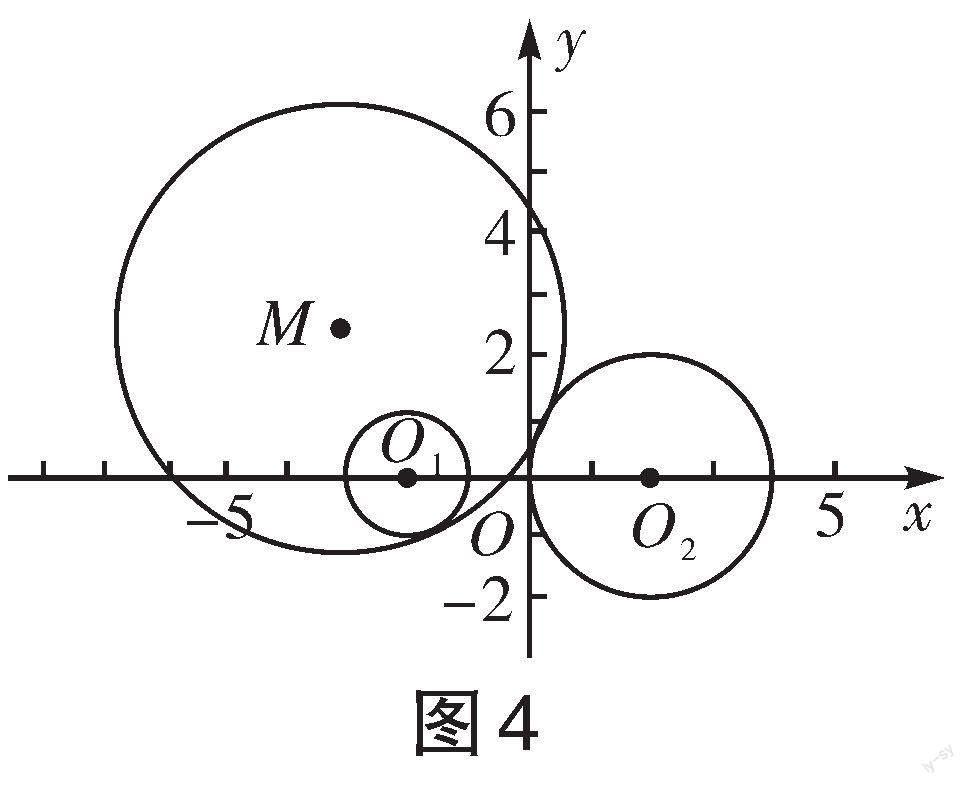
变式2.已知两个定圆[O1]和[O2]，它们的半径分别是1和2，且[O1O2=4]，动圆[M]与圆[O1]内切，也与圆[O2]外切，建立适当的坐标系，求动圆圆心[M]的轨迹方程，并解释轨迹是何种曲线。

分析：利用内切和外切两圆的充要条件，通过分析题目条件，符合双曲线的定义。

解：如图4所示，以[O1O2]的中点[O]为原点，[O1O2]所在直线为[x]轴建立平面直角坐标系。由[O1O2=4]，得[O1（-2，0）]、[O2（2，0）]，设动圆[M]的半径为[r]，则由动圆[M]与圆[O1]内切，有[MO1=r-1]；由动圆[M]与圆[O2]外切，有[MO2=r+2]。

∴[MO2-MO1=3]，

∴点[M]的轨迹是以[O1]、[O2]为焦点，实轴长为3的双曲线的左支。

点评：应用定义法的关键是要熟悉一些基本曲线的定义。比如椭圆、双曲线和抛物线都是圆锥曲线。

三、相关点法

相关点法：又称代入法，即曲线中一个动点[P（x，y）]依赖于另一个动点[Q（x0，y0）]运动，则先假设曲线上任意一点为[P（x，y）]，另外一个相关点为[Q（x0，y0）]，根据条件，列出[x、y]与[x0、y0]的表达式，再反解[x0、y0]，代入[x0、y0]满足的方程，即得动点轨迹方程。

分析：动点[M（x，y）]呈现了一定的规律运动，对于动点[M]所需满足的条件不容易明确或计算。但动点[P]的轨迹已知或易得，可先以 [x0、y0]表示为[x、y]的函数，再将它代入[P]的轨迹方程式，将其整理后得到[M]的轨迹方程。

因此点[P]的轨迹方程为[x2+y2=2]。

点评： 如果点[P] 的运动是由另一点[M] 的运动引起的，而该点的运动规律已知，则可设从动点（求轨迹的动点）为[M（x0，y0）]，主动点（已知曲线上的点）为[P（x，y）]  ，根据这两个点的关系求出曲线的方程。根据从动点与主动点坐标的关系求出曲线方程，需要检验化简后的方程的完备性和纯粹性。

变式3.设[A、B]分别是直线[y=255x]和[y=-255x]上的两个动点，并且[AB=25]，动点[P]满足[OP=OA+OB]，求动点[P]的轨迹[C]的方程。

分析：题目出现了两个动点，而且其中一个动点由另一个动点运动而改变，即可判断可用相关点法。

点评：“相关点法”的基本步骤。

（1）设点。设从动点坐标为[（x，y）]，主动点坐标为[（x1，y1）]；

（3）代换。所求动点的轨迹方程可由已知曲线方程中的变量以关系式表示后求得。

四、参数法

参数法主要是应用在动点横纵坐标关系难以直接建立联系的情况下，引入一个中间变量，用这个中间变量消除参数，得到动点的轨迹方程，常选用的参数有[时间t]、[角度α]、[斜率k等]。

分析：点[P]的运动是由点[A]、点[B]的运动引起的，而[A]、[B]的变动又和斜率有关，所以可选直线的斜率为参数。

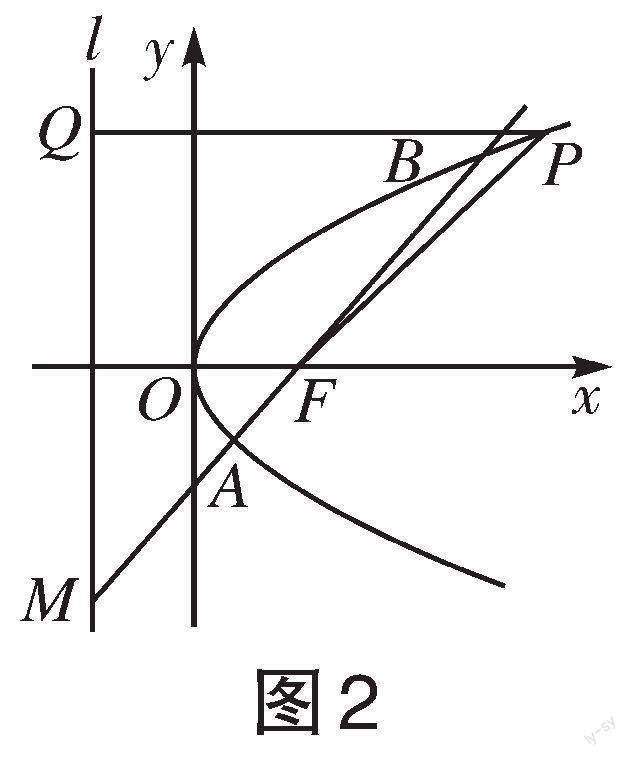
解：设[P（x，y）]，[A（x1，y1）]，[B（x2，y2）]，过点（0，1）的直线为[y=kx+1]，

点评：本题通过引入参数、用参数法求解较为简捷。应用参数法求轨迹方程时，要选择恰当的参数，参数必须能刻画动点的运动变化，并且与动点坐标有直接的内在联系，选定参数之后，即可当作已知数，运用轨迹条件，求出动点的坐标，即得轨迹的参数方程，消去参数即得轨迹的普通方程。

变式4.已知曲线[C：y=x2]与直线[l：x-y+2=0]交于两点[A（xA，yA）]和[B（xB，yB）]，且[xA<xB]。记曲线[C]在点[A]和点[B]之间那一段[L]与线段[AB]所围成的平面区域（含边界）为[D]。设点[P（s，t）]是[L]上的任一点，且点[P]与点[A]和点[B]均不重合。若点[Q]是线段[AB]的中点，试求线段[PQ]的中点[M]的轨迹方程。

分析：由于点[P]在题目中已经自带了参数，通过参数法，将题目中的条件进行化简，即可得到轨迹方程。

点评：求轨迹方程时，如果其他方法都无法解决，就要大胆设参数，通过题设条件列出动点与参数之间的关系式，列方程后，利用方程组之间的关系消参，求出动点之间的关系式和轨迹方程。参数法的主要解题思想是：设而不求，这样就可以大大减少了繁杂的运算，轻松得出轨迹方程。

五、交轨法

“交轨法”常用于求解两条动直线的交点的轨迹方程。

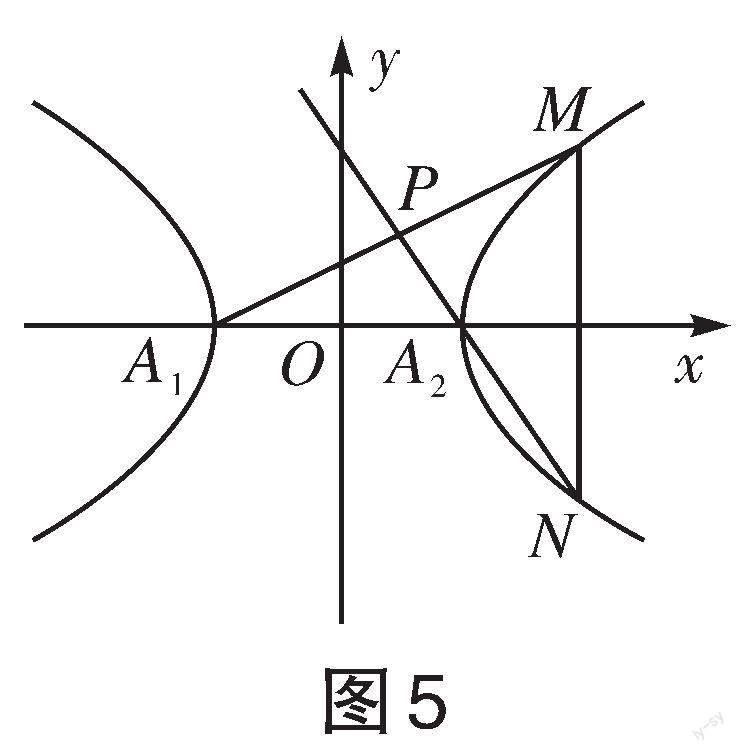
分析：知道了点[P]为两曲线的交点，那么交点方程的求解可采用两种方法。一种是直接用这两条曲线的方程求出交点方程，另一种是先列出交点参数方程的方程组，再转换成一般方程进行求解。哪一种方法更容易实施，就选择哪一种方法。

解：设[P（x，y）]，[M（x1，y1）]，[N（x1，-y1）]，又[A1（-a，0）]，[A2（a，0）]

可得直线[A1M]的方程为：

当[a=b]时，点[P]的轨迹是以原点为圆心、[a]为半径的圆；当[a≠b]时，点[P]的轨迹是椭圆。

点评：如果所求的点是两条曲线的交点，可以试着将两条曲线的方程联立起来，求出交点的轨迹方程，也可以解方程组先求出交点坐标的参数方程，再化作普通的方程。

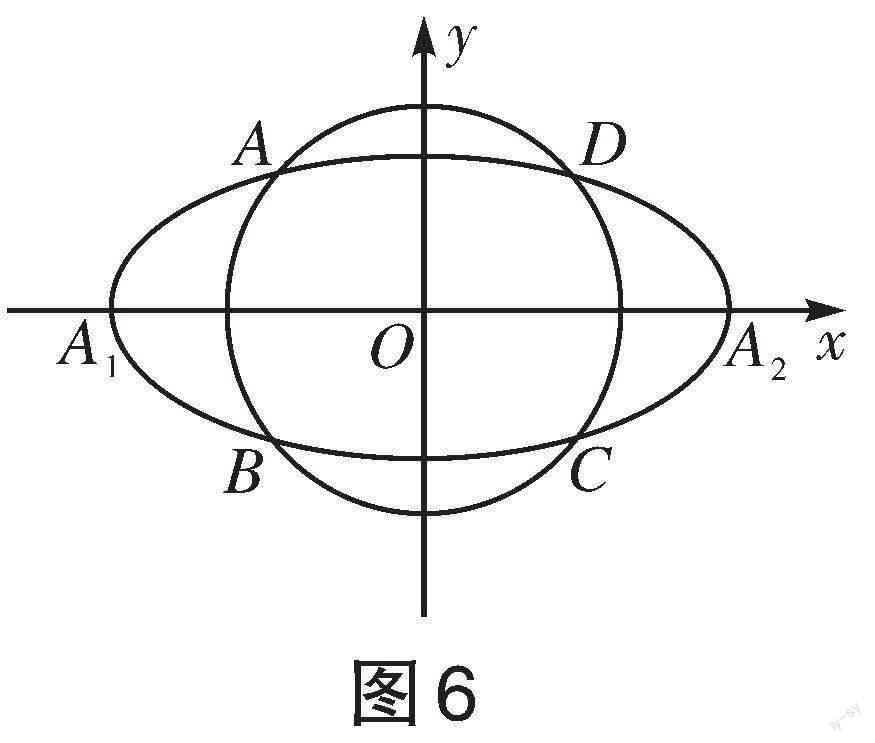
[C0]相交于[A、B、C、D]四点，求直线[AA1]与直线[A2B]交点[M]的轨迹方程。

分析：题目要求的是两直线的交点轨迹问题，故可以用“交轨法”进行求解。

解：设[A（x1，y1）]，[B（x1，-y1）]，又[A1（-a，0）]，[A2（a，0）]，

点评：什么时候选择交轨法，在审題时经常会有很明显的条件指向，比如说求某两种曲线的交点的轨迹等。

六、齐次化法

（1）求椭圆[C]的方程；

（2）过点[P（1，1）]分别作斜率为[k1、k2]的椭圆的动弦[AB]、[CD]，设[M、N]分别为线段[AB、CD]的中点，若[k1+k2=1]，是否存在一个定点[T]，使得其在直线[MN]上，若存在，求出该定点的坐标；若不存在，请说明理由。

分析：本题可以观察中点弦中点与斜率的关系，然后齐次化。

［   参   考   文   献   ］

［1］  杨健茹.高中数学探求轨迹方程的常用技法［J］.科技创新导报，2014（15）：256.

［2］  谢春娥，肖凌戆.基于优效课堂的数学复习课的课堂评价研究［J］.中国数学教育，2020（8）：42-46.