幂函数学习要重视的几个要点

巩丰贤

(山东省淄博市体育运动学校)

幂函数是重要的基本初等函数之一,也是高考命题的重要考点,其中主要涉及幂函数的概念、性质、图像以及与幂函数有关的组合函数或复合函数的性质问题.下面针对这几个要点举例说明,供同学们复习时参考.

1 幂函数的定义

形如f(x)＝xα的函数称为幂函数,其中x是自变量,α∈R,人教A 版教材《数学必修第一册》中给出了具有代表性的5个α值,即α＝1,2,3,,－1,对应的函数为,根据函数解析式求出函数的定义域,画出函数的图像,再研究函数的性质.据此类推,我们也可得出当α＝4,5,,－2,…时,相应的幂函数及性质.

例1下列函数为幂函数的是( ).

A.y＝3xB.y＝(x≠0)

C.y＝－x2D.y＝x0(x≠0)

解析对于选项A,自变量在指数位置,为指数函数;对于选项B,底数与指数中均含自变量,不属于幂函数;对于选项C,y＝－x2为二次函数,不属于幂函数;对于选项D,幂函数的指数可以为0,此时x≠0,故选D.

点评此类问题只要把握好幂函数的定义,即其中底数为自变量,指数为常数,系数为1,即可直接判断.

2 幂函数的性质

当α取不同值时,幂函数具有不同的性质,通过对这 5个函数的性质探究,不难得出幂函数的共性:幂函数的图像过定点(1,1),在(0,＋∞)上都有意义,当α＞0时,函数在(0,＋∞)上单调递增;当α＜0,函数在(0,＋∞)上单调递减.

例2已知幂函数f(x)＝,若f(a＋1)＜f(10－2a),则a的取值范围是_________.

点评此类问题的求解要注意函数的定义域,即a＋1＞0,10－2a＞0.

例3已知函数f(x)的定义域为D,给了下列三个条件:

①∀x∈D,f(x)＋f(－x)＝0;

②∀x∈D,f′(x)≤0;

③∃x1,x2∈D,x1＜x2,使得f(x1)＜f(x2).

试写出一个同时满足条件①②③的函数,则f(x)＝_____.

点评对于条件②和③,同学们可能认为其中存在矛盾.原因是错误地认为f′(x)≤0,则函数单调递减,注意f′(x)≤0是函数f(x)单调递减的必要不充分条件.

3 幂函数之间的关系

将几个幂函数的图像画在同一个平面直角坐标系中,不难发现,当α＞0时,α越大,在(0,1)上,图像离x轴越近,在(1,＋∞)上,图像离x轴越远.这些关系常常成为高考命题的重要视角.

例4已知使得方程f(x)－t＝0有两个实根,则实数m的取值范围是( ).

A.(－∞,0)∪(0,1) B.(0,1)

C.(－∞,0)∪(1,＋∞) D.(1,＋∞)

解析方程f(x)－t＝0有两个实根,即存在直线y＝t与y＝f(x)的图像有两个交点,进而可知函数f(x)不单调.

当m＜0时,函数f(x)的图像如图1所示,存在直线y＝t与y＝f(x)的图像有两个交点,即方程f(x)－t＝0有两个实根.

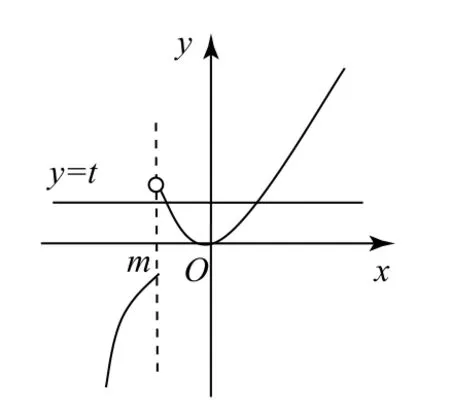
图1

当m＞1时,函数f(x)的图像如图2所示,存在直线y＝t与y＝f(x)的图像有两个交点,即方程f(x)－t＝0有两个实根.

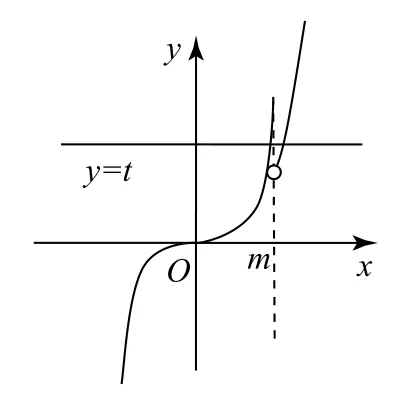
图2

综上,m的取值范围是(－∞,0)∪(1,＋∞),故选C.

点评y＝x2,y＝x3的公共点是(0,0),(1,1),在(0,1)上,x2＞x3;在(1,＋∞)上,x2＜x3.此类问题的求解关键是把握好同类函数的公共点.

4 幂函数的组合

幂函数的组合函数主要有二次函数y＝ax2＋bx＋c(a≠0)、三次函数y＝ax3＋bx2＋cx＋d(a≠0)、双曲线函数等,这些函数都是高考命题中常考的函数类型.

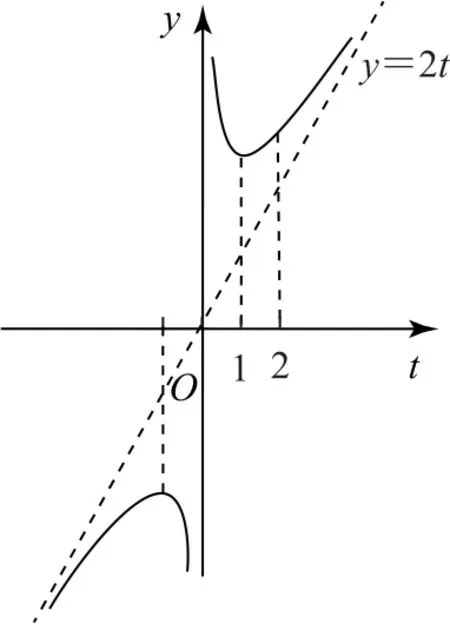
图3

点评在得出函数后,部分同学可能会直接利用均值不等式得出函数的最小值为4,但检验会发现等号成立的条件不在函数的定义域内,故应结合函数f(t)的性质求解.

5 幂函数的复合

形如y＝f[g(x)]的函数,称为复合函数,y＝f(t)为外函数,t＝g(x)为内函数,f(x)的定义域与g(x)的值域交集非空.将两个函数复合在一起,往往可得到较新颖的函数.

点评本题将两个幂函数复合在一起,通过两边取对数构造新函数,从而求函数的最值.

除了上述要点外,解题时还需关注幂函数与其他函数的综合,如,…等超越函数模型,这些函数是高考命题常常涉及的背景函数,因此要熟练掌握这些函数的图像、性质.

(完)