点在面内的多视角证明与高观点审视——一道2020年立体几何高考题引发的探究

李鸿昌

(北京师范大学贵阳附属中学,北京 550081)

题目(2020年高考全国Ⅲ卷理科第19题)如图1,在长方体ABCD-A1B1C1D1中,点E,F分别在棱DD1,BB1上,且2DE=ED1,BF=2FB1.

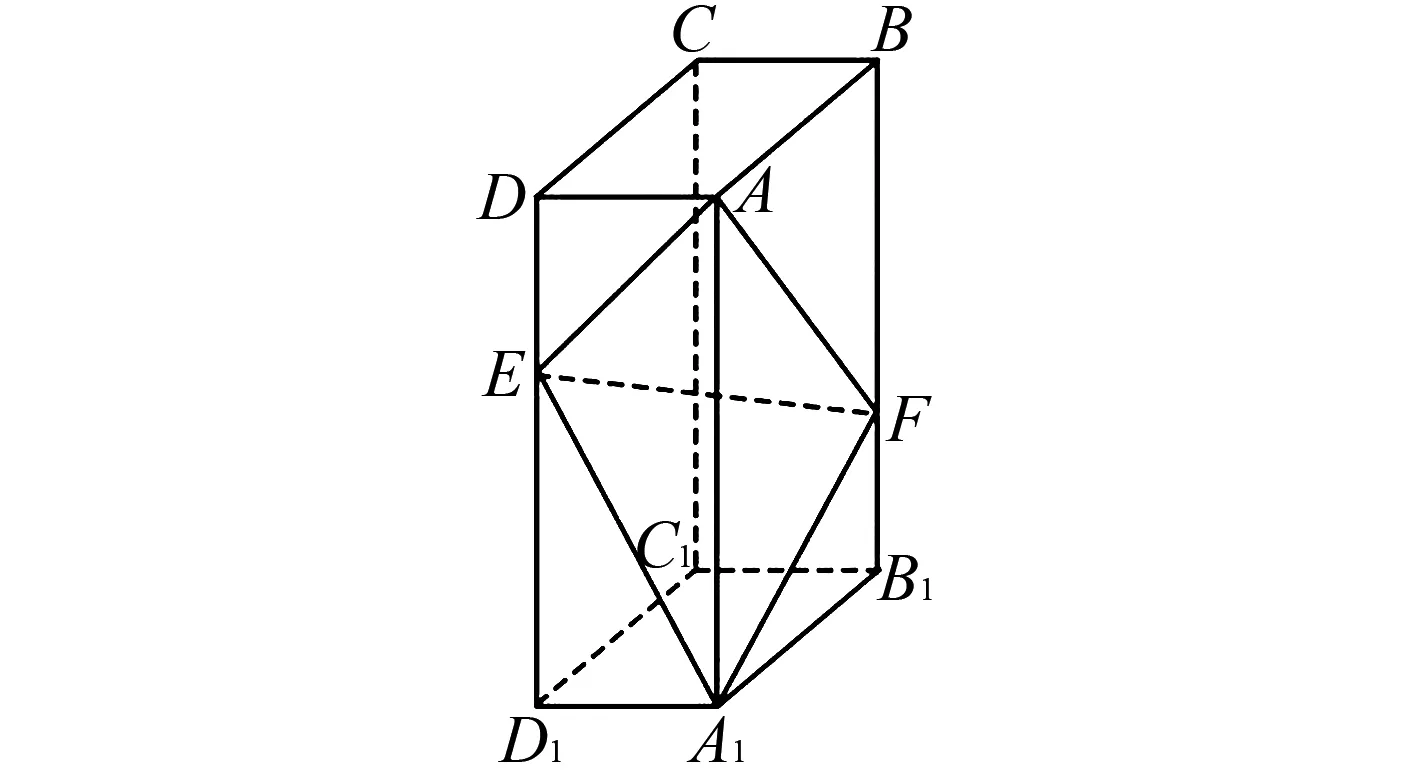
图1 2020年高考全国Ⅱ卷理科19题图

(1)证明:点C1在平面AEF内;

(2)若AB=2,AD=1,AA1=3,求二面角A-EF-A1的正弦值.

1 考题分析

第(1)问是证明点在面内,此问具有很强的创新性与开放性,给考生很大的发挥空间:可以从几何的角度进行证明,也可以从向量的的角度进行证明.第(2)问是求二面角,是常规题,建立空间直角坐标系,求出两个面的法向量即可.

下文主要探究第(1)问的多角度证明与高观点审视.

2 题目解析

视角1经过两条平行直线,或经过两条相交直线,有且只有一个平面.

解法1 如图2,连接EC1,FC1,在AA1上取一点G,使得A1G=2GA,并连接EG,GB1.

图2 解法1图

在长方体ABCD-A1B1C1D1中,易知EG∥D1A1,EG=D1A1,C1B1∥D1A1,C1B1=D1A1.

所以EG∥C1B1,EG=C1B1.

即四边形EGB1C1是平行四边形.

所以EC1∥GB1.

在长方体ABCD-A1B1C1D1中,易知AG∥FB1,AG=FB1.即四边形AGB1F是平行四边形.

所以AF∥GB1.所以EC1∥AF.

所以A,E,C1,F四点共面[1].

故点C1在平面AEF内.

解法2 如图3,连接EC1,FC1,在AA1上取一点M,使得AM=2MA1,并连接D1M,MF.

图3 解法2图

在长方体ABCD-A1B1C1D1中,易知MF∥A1B1,MF=A1B1,A1B1∥D1C1,A1B1=D1C1.

所以MF∥D1C1,MF=D1C1.

即四边形MFC1D1是平行四边形.

所以MD1∥C1F.

在长方体ABCD-A1B1C1D1中,易知ED1∥AM,ED1=AM.即四边形ED1MA是平行四边形.

所以AE∥MD1.所以AE∥C1F.

所以A,E,C1,F四点共面.

故点C1在平面AEF内.

解法3 如图4,延长AE,A1D1交于点M,延长AF,A1B1交于点N,连接MN,MN与直线D1C1交于点O.

图4 解法3图

因为2DE=ED1,BF=2FB1,DE∥AA1,FB1∥AA1,

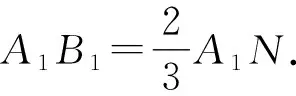
又因为D1O∥A1N,

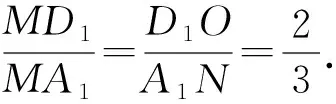
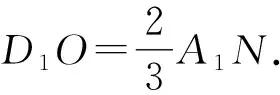
又因为A1B1=D1C1,所以D1O=D1C1.

则点O与C1重合.

即C1在直线MN上.

因为MN⊂平面AEF,C1∈MN

所以点C1在平面AEF内.

视角2向量共面定理.

由共面向量的充要条件知,A,E,C1,F四点共面.

故点C1在平面AEF内.

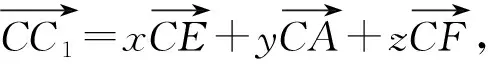
即x+y+z=1.

由共面向量的充要条件知,A,E,C1,F四点共面.

故点C1在平面AEF内.

图5 解法6图

由共面向量的充要条件,知A,E,C1,F四点共面.

故点C1在平面AEF内.

视角3 点面距.

若点到平面的距离为0,则点在平面内.

设平面AEF的法向量为n=(x0,y0,z0),

令z0=3ab,得n=(-2bc,-ac,3ab).

设C1到平面AEF的距离为h,则

即点C1到平面AEF的距离为0.

所以点C1在平面AEF内.

视角4 线面角.

若直线与平面所成的角是零角,且直线有一个点在平面内,则直线在平面内.

解法8同解法7,得平面AEF的法向量

设直线AC1与平面AEF所成的角为θ,则

即直线AC1与平面AEF所成的角为0.

又A∈平面AEF,

所以AC1⊂平面AEF的.

故点C1在平面AEF内.

视角5 法向量垂直于平面内的任意直线.

解法9同解法7,得平面AEF的法向量

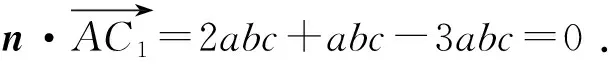
又因为点A∈平面AEF,

所以AC1⊂平面AEF.

所以A,E,C1,F四点共面.

故点C1在平面AEF内.

3 高考真题探源

在往年的高考真题中,是否出现过证明四点共面的试题呢?或者与之相似的试题呢?

其实,我们可以在往年的高考真题中找到四点共面的原型.那就是2019年全国Ⅲ卷理科第19题的第(1)问和2019年北京卷理科第16题的第(3)问[2].

(2019年全国Ⅲ卷理19)图6是由矩形ADEB,Rt△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°,将其沿AB,BC折起使得BE与BF重合,连接DG,如图7.

图6 2019年全国Ⅲ卷理19题图 图7 2019年全国Ⅲ卷理19题图

(1)证明:图7中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;

(2)求图7中的二面角B-CG-A的大小.

证明(1)由已知得AD∥BE,CG∥BE.

所以AD∥CG.

故AD,CG确定一个平面.

从而A,C,G,D四点共面．

高考真题是高考命题专家智慧的结晶,经典而具有代表性,很多的高考题都可以在往年的真题中找到原型.因此,在高三备考复习中,做真题卷,对历年高考真题进行变式、推广等研究很有必要.

4 高观点审视

4.1 平面方程

设平面的法向量为n=(A,B,C),且过点(x0,y0,z0),因为一个点和一个法向量决定一个平面,所以得到平面点法式方程

A(x-x0)+B(y-y0)+C(z-z0)=0.

在平面点法式方程中,令D=-Ax0-By0-Cz0,则得到平面一般式方程Ax+By+Cz+D=0.

4.2 求平面方程

由上文知,平面AEF的法向量n=(-2bc,-ac,3ab)且过点A(a,b,c),由平面点法式方程得

-2bc(x-a)-ac(y-b)+3ab(z-c)=0.

化简,得-2bcx-acy+3abz=0.

即为平面AEF的方程.

4.3 证明点在面内

思路1 检验点的坐标是否满足平面方程.

解法10 因为点C1(0,0,0),显然满足平面AEF的方程-2bcx-acy+3abz=0.

所以点C1在平面AEF内.

思路2计算点面距是否为0.

4.4 三向量共面的充要条件

三向量共面当且仅当它们的混合积为零,当且仅当它们的坐标构成的行列式为零.

证明设向量mi(i=1,2,3)的坐标是(ai1,ai2,ai3),i=1,2,3.此三向量共面当且仅当它们共起点时构成的平行六面体体积为零,当且仅当(m1,m2,m3)=0,当且仅当

4.5 空间四点共面的充要条件

空间四点A(x1,y1,z1),B(x2,y2,z2),C(x3,y3,z3),D(x4,y4,z4)共面当且仅当

利用空间四点共面的充要条件可得到该问题的另一高观点解法.

=0,

所以A,E,F,C1四点共面.

故点C1在平面AEF内.