一道求空间点到直线距离试题的七种解法
王恩普
(江苏省淮阴中学教育集团淮安市新淮高级中学,江苏 淮安 223001)
在“三新”背景下,教材显然是一线教师和学生的主阵地,教材的研究显得尤为重要,尤其是教材中的例题和习题,都是精编细选,深得很多命题者的青睐,因此有必要对一些典型的例习题进行深入探究.本文从不同的视角出发,对苏教版选择性必修第二册中的一道例题的解法进行了充分研究,而且在解法探究的过程中,也很自然地体现了基础性、综合性和创新性.
1 试题呈现
题目如图1,已知正方体ABCD-A1B1C1D1的棱长为1,E,F分别是BC和CD的中点.求点E到直线B1D1的距离.

图1 题目示意图
这是苏教版选择性必修第二册6.3.4《空间距离的计算》例11的改编,考查空间几何中的点到直线的距离,此题的背景是正方体,坐标表示较为简单,但是从不同的视角出发,可以发现解法多样,各具特点,因此文章对本题的解法进行了深入研究,与读者共享.
2 解法探究


图2 空间直角坐标系示意图





令x=1,则y=-1,z=4.
解得n=(1,-1,4).
故点E到直线B1D1的距离为



故点E到直线B1D1的距离为


设平面EB1D1的一个法向量为
n1=(x1,y1,z1),


令x1=2,得z1=-1,y1=-2.
所以n1=(2,-2,-1).
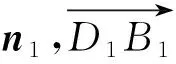
n2=(x2,y2,z2),


令x2=1,得y2=-1,z2=4.
可得n2=(1,-1,4).
故点E到直线B1D1的距离即为
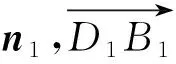
解法4 (求空间向量的模)如图3,在平面EB1D1内过点E作直线B1D1的垂线,垂足为点H,由平面向量基本定理,知

图3 解法4示意图
又H,B1,D1三点共线,则有λ+μ=1.





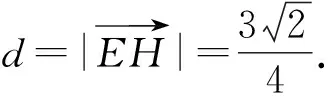



由投影向量,知
评注解法5来源于人教版教材,借助于投影向量的概念,问题解决过程简洁,易操作.

由余弦定理,知


评注解法6把空间的点到线的距离转化为平面三角形中的高,只需要求出三角形的三边长,借助于三角函数知识即可解决,从而体现了转化与化归思想.
解法7(两点距离公式)如图3,在平面EB1D1内过点E作直线B1D1的垂线,垂足为点H,由题可设H(x,x,1),则


故点E到直线B1D1的距离为

评注解法7的本质就是设出垂足的坐标,通过向量的数量积表示出垂直关系,从而求出垂足的坐标,然后利用空间两点距离公式即可求解.
3 教学启示
在新高考形势下,对学生的考查应该是全方面的,所以对于问题的解决,不能仅限于得出结果,更重要的是要在解题中提升学生的能力,并能引导学生打破常规进行独立思考和判断,提出解决问题的方案,主动从不同的角度进行探究,融合所学知识,在数学学习过程中培养学生的思维品质,提高学生分析问题、解决问题的能力[1].

