二面角问题的综合几何法运用
蔡毅锡
(佛山市南山湖实验中学,广东 佛山 528031)
在历年的高考数学中,立体几何主观解答题往往不会缺席,近三年,该题型的命题特点与考查形式呈现了一定规律.本文对此进行了总结,从结论来说,该题型提高了学生对综合几何法的掌握要求,并仍以二面角问题为难点设问.为让师生更好地应对该题型,本文提供了通过综合几何法解决简单二面角问题的解题方案,并探讨了综合几何法的学习意义与教学建议.
1 新高考下二面角问题的命题特点
1.1 立体几何主观解答题的命题特点
近三年,立体几何主观解答题一般位于高考数学试卷的第18~20题的位置,设两个小问.第一问往往是考查线面平行、面面平行、线面垂直、面面垂直等位置关系的证明.偶见考查棱锥、棱柱体积的计算,以及点到平面的距离计算,但频率较前者要小.第二问往往是考查经典线面角或二面角的相关计算,在广东省选用的全国Ⅰ卷中,往往考查二面角的相关计算,亦有“全国爱考二面角,浙江爱考线面角[1]”的说法.
1.2 立体几何主观解答题的考查形式
根据《普通高中数学课程标准》的要求,学生应能运用向量运算解决简单的几何问题,掌握基本空间图形及其简单组合体的概念和基本特征,能证明简单的几何命题并进行简单运用.
简而言之,即学生应掌握解决高中阶段立体几何问题中常用到的综合几何法和空间向量法,并体会两种方法的共性与差异.
回顾近三年的新高考,其立体几何主观解答题都能很好地贴合要求,考查了学生的综合几何法和空间向量法的掌握程度.但题目的图形载体倾向于简单几何体(柱、锥、台)或不规则几何体[2],少见长方体等易于直接建立空间直角坐标系的几何体,这使得学生不能直接建系后依靠空间向量法解决问题.下面举出两个例子说明:
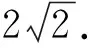

图1 2022年全国Ⅰ卷19题图
(1)求A到平面A1BC的距离;
(2)设D为A1C的中点,AA1=AB,平面A1BC⊥平面ABB1A1,求二面角A-BD-C的正弦值.
例2(2021年全国Ⅰ卷20题)如图2,在三棱锥A-BCD中,平面ABD⊥平面BCD,AB=AD,O为BD的中点.

图2 2021年全国Ⅰ卷20题图
(1)证明:OA⊥CD;
(2)若△OCD是边长为1的等边三角形,点E在棱AD上,DE=2EA,且二面角E-BC-D的大小为45°,求三棱锥A-BCD的体积.
以上是近两年数学高考全国Ⅰ卷的立体几何主观解答题.虽然图形是简单几何体,但从题目的已知条件可知,学生不能直接建立空间直角坐标系进行解题,而是需要通过综合几何法证明出关键的线线垂直后才能建系,明显提高了学生对综合几何法的掌握要求.
2 综合几何法解二面角问题
面对二面角问题,目前的教学以空间向量法为主.空间向量法对于解决二面角问题固然高效,但综合几何法解决二面角问题时,对于学习二面角这个几何图形有着较大的帮助.下面介绍综合几何法解决二面角问题的步骤、要点与示例.
2.1 解法要点
本法解决二面角问题,依然需要按照“作、证、求”四步完成.
第一步:找出与二面角其中一个半平面垂直的平面.大多数二面角问题都会存在这样一个平面,它与二面角其中一个半平面垂直,而这是使用本法的标志和开端(例如例1中,存在平面ABB1A1与二面角的其中一个半平面A1BC垂直).
第二步:利用面面垂直构造二面角的平面角.此为“作、证、求”三步中的“作”.如图3,假设第一步中,存在平面γ′垂直于二面角的其中一个半平面β,记A为平面γ′与二面角的另一个半平面α的其中一个交点.过点A作h⊥l′,其中l′=γ′∩β,h∩β=C.过点C在平面β内作CO⊥l(l指二面角的棱),连接AO,则∠AOC为二面角A-l-B的平面角(或过点A在平面α内作AO⊥l,后连接CO).

图3 二面角解法示意图
第三步:证明二面角的平面角.此为“作、证、求”三步中的“证”.
因为γ′⊥β,γ′∩β=l′,h⊥l′,所以h⊥β.
又因为CO,l⊂β,所以h⊥CO,h⊥l.
因为CO⊥l,h⊥l,CO∩h=C,
所以l⊥平面AOC.
因为AO⊂平面AOC,所以l⊥AO.
故∠AOC为二面角A-l-B的平面角.
第四步:求二面角的平面角.此为“作、证、求”三步中的“求”.
在第三步中证明了h⊥l,所以△AOC是直角三角形.直角三角形中能够运用勾股定理,也能简单地计算其中一个内角的三角函数值,这为最终解决二面角问题提供了极大的便利.
2.2 解法示例
例1第(2)问解析
过点A作AE⊥A1B交A1B于点E.过点E作EF⊥BD交BD于点F.连接AF.因为平面A1BC⊥平面ABB1A1,平面A1BC∩平面ABB1A1=A1B,AE⊥A1B(识别出平面ABB1A1垂直于二面角的其中一个半平面A1BC),所以AE⊥平面A1BC.
又因为EF,BD⊂平面A1BC,所以AE⊥EF,AE⊥BD.因为EF⊥BD,AE∩EF=E,所以BD⊥平面AEF.
因为AF⊂平面AEF,所以BD⊥AF.
故∠AFE为二面角A-BD-C的平面角.(至此处已按照方法完成了二面角的“作”与“证”,如图4)

图4 2022年全国Ⅰ卷19题第(2)问题图
因为AE⊥平面A1BC,BC⊂平面A1BC,所以AE⊥BC.又因为直三棱柱ABC-A1B1C1中易证AA1⊥BC,AE⊥BC,AA1∩AE=A,所以BC⊥平面ABB1A1.
因为AB,A1B⊂平面ABB1A1,所以BC⊥AB,BC⊥A1B.因为AA1=AB,AE⊥A1B,所以A1E=EB.

因为VABC-A1B1C1=4,AA1=2,所以S△ABC=2.
所以BC=2.
因为∠EAF=∠BA1C,EF⊥BD,BC⊥A1B,
所以△BEF∽△A1CB.

在Rt△AEF中
例2第(2)问解析
过点E作EG⊥BD交BD于点G,过点G作FG⊥BC交BC于点F.连接EF.因为平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,(识别出平面ABD垂直于二面角的其中一个半平面BCD),所以EG⊥平面BCD.又因为BC,FG⊂平面BCD,所以EG⊥BC,EG⊥FG.因为BC⊥GF,BC⊥EG,EG∩FG=G,所以BC⊥平面EFG.因为EF⊂平面EFG,所以BC⊥EF.故∠EFG为二面角E-BC-D的平面角,∠EFG=45°.(同上例,至此处已按照方法完成了二面角的“作”与“证”,如图5)

图5 2021年全国Ⅰ卷20题第(2)问题图
又因为EG⊥FG,所以EG=FG.
因为AO⊥BD,EG⊥BD,∠ADB=∠ADB,
易证△AOD∽△EGD.

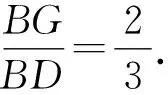
因为△OCD是边长为1的等边三角形,且BO=OD,易证△BCD是直角三角形,∠BCD=90°,∠BDC=60°.
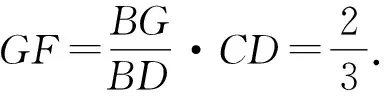
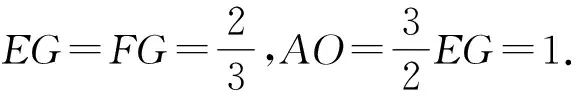
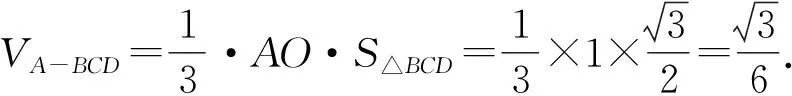
相较于代数问题,几何问题更显灵活性,学生在面对不同图形载体下的几何题目时,往往易出现不知从何入手的问题.尽管立体几何问题浩如烟海,图形载体千题千样,但在实际教学中,应该尽可能地将同类题型、问法归类整理,总结出1~2条常见且行之有效的解题思路供同学们参考,减少学生常凭灵感解题的情况.长此以往,学生通过大量成功的解题练习,既能在不断地练习中巩固基础知识、锻炼解题技巧,又能增强立体几何的学习信心.

