一道八省联考解析几何题的解法探秘

鲁和平

(浙江省嘉善第二高级中学,浙江 嘉兴 314100)

题目(2021年八省联考数学试题第7题)如图1,已知抛物线y2=2px上三点A(2,2),B,C.直线AB,直线AC是圆N:(x-2)2+y2=1的两条切线,则直线BC的方程为( ).

图1 2021年八省联考第7题图

A.x+2y+1=0 B.3x+6y+4=0

C.2x+6y+3=0 D.x+3y+2=0

1 题目解析

解法1(直译法) 将A(2,2)代入y2=2px,得p=1.

故抛物线方程为y2=2x.

设过A(2,2)的切线方程为

y-2=k(x-2).

即kx-y+2-2k=0.

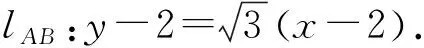
代入y2=2x,整理,得

故yB+yC=-4.

即3x+6y+4=0.

故选B.

解法2(韦达定理法)

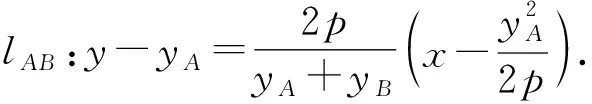
即2px-(yA+yB)y+yAyB=0.

这里p=1,xA=2,yA=2,

故lAB:2x-(2+yB)y+2yB=0.

因为直线AB与圆N:(x-2)2+y2=1相切,

①

②

由①②可知:yB,yC是方程3y2+12y+8=0的两个不等的实根,

代入2x-(yB+yC)y+yByC=0,得

直线BC的方程为3x+6y+4=0.

解法3(轨迹法) 由解法2知

3·(2xB)+12yB+8=0.

即3xB+6yB+4=0.

③

同理可得3xC+6yC+4=0.

④

由③④可知

点B与点C均在直线3x+6y+4=0上.

故直线BC的方程为3x+6y+4=0.

代入y2=2x整理,得

由两点式得直线BC的方程为3x+6y+4=0.

解法5(抛物线参数方程法)因为抛物线方程为y2=2x,设B(2t2,2t),

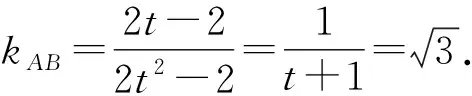
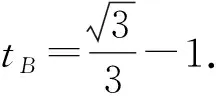
由两点式得直线BC的方程为3x+6y+4=0.

图2 张角定理图 图3 解法6图

代入y2=2x整理,得

如图3,由张角定理,得

将点E坐标代入四个选项,检验知B正确.

解法7(导数法) (1)首先证明以下命题:

已知抛物线C:y2=2px,定点A(x0,y0)∈C,动点P(x1,y1)∈C,Q(x2,y2)∈C,kAP+kAQ=0,则kPQ为定值,且等于抛物线在点A处切线斜率的相反数.

代入kAP+kAQ=0整理,得2p(y1+y2+2y0)=0.

故y1+y2=-2y0.

又因为y2=2px,所以2yy′=2px.

所以kPQ=-kA.故命题得证.

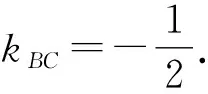
由直线的点斜式方程,得

BC的方程为3x+6y+4=0.

(2)如图4,作出点A关于x轴的对称点A1(2,-2).

图4 解法7(2)示意图

由y2=2x得抛物线的下半支的方程为

所以过点A1(2,-2)的切线的斜率为

由拉格朗日中值定理,知

由点斜式得直线BC的方程为

3x+6y+4=0.

故直线BC的方程为

整理,得x-(b+c)y+2bc=0.

所以b,c是方程3x2+6x+2=0的两根.

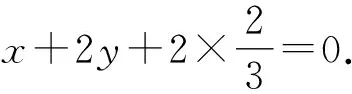
即3x+6y+4=0.

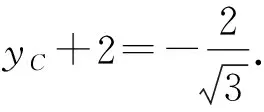
由点斜式得直线BC的方程为3x+6y+4=0

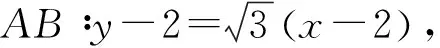
则由AB,AC构成的二次曲线方程为

化简,得3(x-2)2-(y-2)2=0.

代入上式,得(y-2)2(3y2+12y+8)=0.

将y2=2x代入,得

(2x-4y+4)·(6x+12y+8)=0.

又因为过点A的切线方程为x-2y+2=0,

且直线AB,AC构成的曲线与抛物线的交点是A,B,C三点,

所以直线BC的方程为3x+6y+4=0.

解法10(待定系数法)由抛物线,直线AB,AC构成的二次曲线方程为

①

化简整理,得

-3λx2+(λ+μ)y2+(12λ-2μ)x-4λy-8λ

=0.

因为过点A的切线方程为x-2y+2=0,

设直线BC:ax+by+c=0,

则由过点A的切线、直线BC构成的二次曲线方程可设为

(x-2y+2)(ax+by+c)=0.

化简整理,得

ax2-2by2+(b-2a)xy+(c+2a)x+(2b-2c)y+2c=0.

②

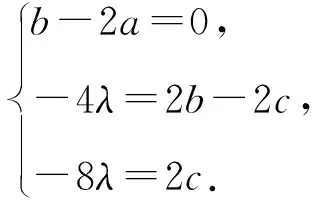
即3x+6y+4=0.

数学学习离不开解题的研究,而对于数学问题的解决不能仅停留于得出答案层面,更重要的是引导学生进行多向思维[1].同一题目从不同角度进行研究往往会有不同的发现,进而会有不同的解题方法,所以应在拓展思路的过程中培养学生的发散思维,结合题目中的已知条件发现解决问题的关键,并有效地巩固基础知识,掌握解题技巧,提高学生分析问题、解决问题的能力.