从一道联考试题谈米勒定理及其简单应用
陈艺平
(福建省龙海第一中学,福建 漳州 363100)
米勒问题涉及三角形、直线、圆、椭圆、双曲线等众多知识点,经常与角度的最值问题结合考查.借助米勒定理可以迅速求解此类角度的最值问题.
1 试题呈现
题1 (华南师大附中,广东省实验中学,广雅中学,深圳中学2022届高三四校联考第7题)在足球比赛中,球员在双方球门前的不同的位置起脚射门对球门的威胁是不同的,出球点对球门的张角越大,射门的命中率就越高.如图1为室内5人制足球场示意图,设球场(矩形)长BC大约为40米,宽AB大约为20米,球门长PQ大约为4米.在某场比赛中有一位球员欲在边线BC上某点M处射门(假设球贴地直线运行),为使得张角∠PMQ最大,则BM大约为( )(精确到米).
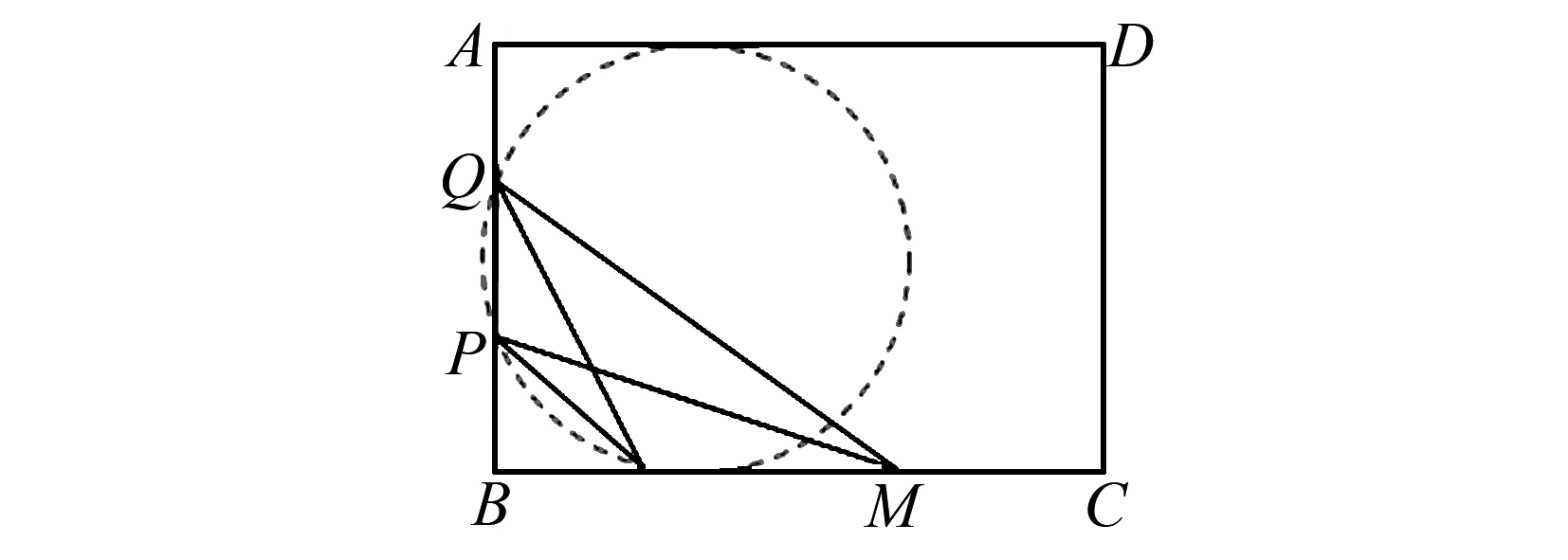
图1 2022届高三四校联考第7题图
A.8 B.9 C.10 D.11
2 试题分析
本题以5人制足球场为背景,求足球运动员最佳射门位置.显然这是一道现实生活中的问题,体现了数学来源于现实并用于解决实践问题的理念,突出了对数学建模素养的考查.试题入手宽,解法多,但是不同的解法繁简程度不一,要求考生择优选择最佳路径解决问题,突出了对数学运算素养的考查.
3 试题解析
思路1 从解析几何的角度入手.如图1所示,要使得张角∠PMQ最大,即tan∠PMQ最大.从函数的观点来看,要解决最值问题,必须引入变量,即将tan∠PMQ表示成某个变量的函数,再借助函数求最值的方法解决问题.观察图1可知,∠PMQ=∠BMQ-∠BMP,所以可以将tan∠PMQ转化成tan(∠BMQ-∠BMP).进一步借助两角差的正切公式展开并引入变量解决问题.
解法1 设BM=x,x∈(0,40],
tan∠PMQ=tan(∠BMQ-∠BMP)
当且仅当x2=96,即x≈10时,tan∠PMQ取得最大值.
此时张角∠PMQ最大,所以当BM大约为10米时,张角∠PMQ最大.
思路2 思路1虽然解法自然,但是计算量大,同时也没有看到试题背后隐含的本质.本题要寻找最佳射门位置,实则是著名的米勒问题[1].米勒是德国的一名数学家,他于1471年提出一个有趣的问题:在地球表面的什么位置,一根垂直的悬杆呈现最长?即在什么位置,视角最大?这个问题被称为最大视角问题,又称之为“米勒问题”.其数学表述如下:
已知点A,B是∠MON的边ON上的两个定点,点C是边OM上的动点,则当点C在何处时,∠ACB最大?
可以证明如下结论:
已知点A,B是∠MON的边ON上的两个定点,点C是边OM上的动点,则当且仅当△ABC的外圆与边OM相切于点C时,∠ACB最大.
该结论简称为米勒定理.主要有以下三种模型.
模型1 如图2所示,设直线a//b,直线a上有两个定点M,N.在直线b上取一个动点P,则当点P位于过点M,N的圆与直线b相切的切点时,∠MPN最大,此时PM=PN.

图2 模型1图 图3 模型2图 图4 模型3图
模型2 如图3所示,设直线a和b相交于点O,直线a上有两个定点M,N.在直线b上取一个动点P,则当点P位于过点M,N的圆与直线b相切的切点时,∠MPN最大,此时OP2=OM·ON.
模型3 如图4所示,设直线a与圆O1相切于点Q,直线a上有两个定点M,N.动点P在圆O1上运动,则当点P位于过点M,N的圆O2与圆O1相切的切点时,∠MPN最大.
运用该定理可以解决数学上一些与最大角有关的问题.因此对于本题,还可以有如下解法.

显然思路2比思路1在思维上更胜一筹,在计算上更加简捷,体现了多思少算的良好数学品质.这也体现了命题者命制本道试题的初衷——对数学建模思想的考查。
4 拓展应用

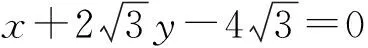

图5 2022年上海交大强基试题图

由于QP2=QF2·QF1=45,
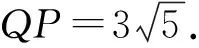

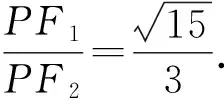
例2(2022年9月清华大学中学生标准学术能力诊断性测试)在平面直角坐标系中,A(0,1),B(0,2),若动点C在直线y=x上,圆M过A,B,C三点,则圆M的面积最小值为____.
解析如图6所示,当圆M与直线y=x相切于点C时, 圆M的面积最小.

图6 例2题解析图
由割线定理可知,OC2=OA·OB=2.
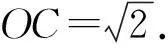
在△BOC中由余弦定理可得BC2=2.
则BC2+OC2=OB2.
所以BC⊥OC.
故BC为圆M的直径.

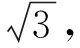
解析由已知可得b=2.
作直线l∥AC,当过A,C两点的圆与直线l相切于点B时,∠ABC最大.结合已知条件易知此时△ABC为正三角形[2].

例4 已知点P为抛物线y2=4x上一动点,A(1,0),B(3,0),则∠APB的最大值为____.
解析根据米勒定理,当点P为过A,B的圆与y2=4x相切的切点时,∠APB取最大值.

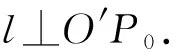
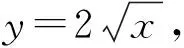
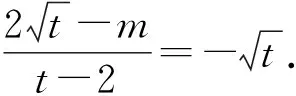

显然P0A⊥AB,
所以△P0AB为等腰直角三角形.





图7 例5题解析图
由切线定理有AP2=AF1·AF2.故AP=b.
此时P(-a,b),F1(-c,0),F2(c,0).
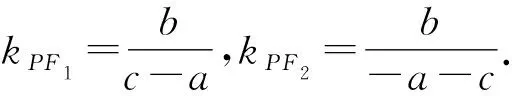

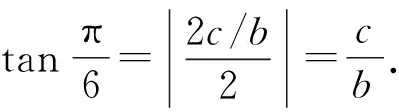



图8 例6题解析图

由于∠BPF1=∠BF2P(弦切角等于所夹弧对应的圆周角),得△BPF1∽△BF2P.

例7 已知点A(-1,0),B(3,0),点P为圆O:x2+y2=45上一个动点,则sin∠APB的最大值为____.
解析如图9所示,设△ABP的外接圆圆心为M(1,t),半径为R.当圆M与圆O相切于点P时,∠APB最大,此时O,M,P三点共线.

图9 例7题解析图

结合OP=OM+MP可得

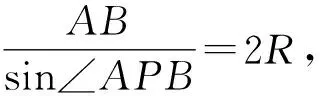


在一些现实问题中,涉及到视野的最大值问题也可以借助米勒定理解决,体现了数学建模的思想.数学建模是六大数学核心素养之一,贯穿于新教材必修一和必修二两册的教学内容当中.数学建模素养是教师在课堂教学中应该着力培养的素养,在平时的教学中教师可以适当介绍米勒问题,并与高中内容相结合,以此为抓手培养建模思想,提高数学思辨智慧,促进深度学习.

