高中物理功能关系解题探究
张海波
(安徽省泗县第一中学,安徽 泗 234300)
功能关系是高中物理学习阶段中复杂程度较大的知识内容,同时,它也是高中物理最为重要的知识内容之一.在高考中,功能关系一般都是在一些大题或者压轴题出现,很多学生在这方面都感受到了学习的困难,如果不加以解决,就会抑制学生的学习信心.所以,在开展功能关系教学时,教师需要结合实际例题来增强学生对这部分知识的学习能力.
1 动能定理应用
动能定理这个知识点是非常好用的一个公式,它的公式可以写成W=EK2-EK1,根据公式学生就能够知道合外力做的功就等于物体末动能与初动能的变化量.这个公式应用十分广泛,并且属于功能关系当中比较重要的内容,因此,在开展教学时,教师就需要对解题的策略进行探究,带领学生更加有效地理解知识点[1].
例1如图1所示,将一个小物块水平抛出,其中小物块的质量m=3 kg,初速度V0=4 m/s,抛出后刚好能够从A点进入到轨道中.已知圆弧轨道的半径为R=3.75 m,圆弧轨道的最低点是B点,并且与BD这个水平轨道平滑连接,A点与圆心O的竖直线夹角为37°,一个粗糙轨道MN,小物块与这个轨道的动摩擦因数值为0.1,其他部分均是光滑的.图中右侧还有一个r=0.4 m的半圆弧轨道,该圆弧轨道的最高点是C,并且在D点与轨道BD做平滑连接.(g=10 m/s2,sin37°=0.6,cos37°=0.8.)

图1 例1题图
(1)在B点时轨道所受到的压力为多少;
(2)如果MN轨道长度L0=6 m,求小在C点时轨道所受到的压力为多少;
(3)如果小物块刚好能到达C点,求MN轨道的长度L.
解析对于动能定理来说,首先需要确定一个过程,然后在去求出该过程的末动能与初动能,接着就是运用动能定理去求出想要的信息,再结合实际问题进行思考,以此能够做到更加高效、有益的教学.
解(1)根据平抛运动的规律,得
V0=VAcos37°,
解得小物块经过A点时的速度大小VA=5 m/s,小物块从A点经过B点,根据动能定理有
小物块经过B点时,有
解得FN=62 N,根据牛顿第三定律,小物块对轨道的压力大小为62 N
(2)小物块由B点运动到C点,根据动能定理,有
小物块在C点,有

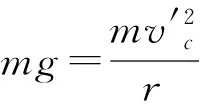
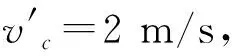
在B点到C点小物块的运动当中,根据动能定理,有
解得L=10 m.
2 机械能守恒定律应用
在只有重力或弹力做功的物体系统内(或者不受其他外力的作用下),物体系统的动能和势能(包括重力势能和弹性势能)发生相互转化,但机械能的总能量保持不变,这个规律叫做机械能守恒定律.机械能守恒定律大都是一些大题的应用,因此,具有一定的解题思路就非常得重要,在课堂上教师可以借助实际的例题,然后带领学生进行实践[2].
例2如图2所示,一重为2 N的小球被一根轻质弹簧和一根细绳共同拉住保持平衡,且此时刚好细绳处于水平位置.如果将细绳剪断,小球运动到弹簧正下方时弹簧的长度正好等于未剪断细绳时弹簧的长度.那么求:小球运动到悬点正下方时向心力的大小.

图2 例2题图
解析首先,结合机械能守恒定律的知识点,学生需要明白的是要如何运用已有的信息进行求解,而对于这道题而言,缺乏了很多的信息,因此,对于解答问题来说,就需要学生去实质性地分析探究,并且利用假设的想法去设几个未知数.
解设弹簧原长为L0,初始状态平衡时弹簧的长度为L,将弹簧与竖直方向的夹角设为θ,小球的质量设为m,开始状态为平衡态,有
k(L-L0)cosθ=mg=2N,
设小球运动到最低点时速度为v,有
线没有烧断时的位置与最低点弹簧长度相同,所以初末位置弹性势能相同,设为EP,由机械能守恒定律,有

综上可以得到,
所以,θ=60°,

所以向心力是:
F向=k(L-L0)-mg=mg=2 N.
3 能量守恒定律应用
能量守恒定律是指在一个封闭的系统当中,总能量总会保持不变,能量不会凭空出现也不会凭空消失,能量之间可以进行转换.在高中物理中的功能关系当中,能量守恒定律是非常重要的,它所涉及到的题型也比较困难和复杂,很多学生都会缺失做题的思路,所以,教师就应该带领学生去探究如何做题,培养解题的思维.
例3 如图3所示,一处滑雪道由AB和BC两段组成,AB是倾角θ=37°的斜坡,BC是半径R=5 m的圆弧面,圆弧面和斜面相切于B,与水平面相切于C,AB竖直高度差h1=8.8 m,竖直台阶CD高度差h2=5 m,台阶底端与倾角θ=37°斜坡DE相连.运动员连同滑雪装备总质量m=80 kg,从A点由静止滑下通过C点后飞落到DE上.不计空气阻力和轨道的摩擦阻力,g取10 m/s2,sin37°=0.6,cos37°=0.8.求:

图3 例3题图
解(1)A→C过程中,由动能定理
联立可得:vc=14 m/s.
(2)对C点,由牛顿第二定律,
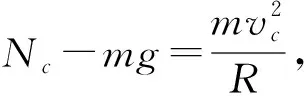
(3)设在空中时间为t,有
所以t=2.5 s,t=-0.4 s(舍).
总之,对于高中物理的功能关系题型来说,这一部分难度是非常大的,如果不加以合理的教学,很多学生都会在此受到影响或抑制,最终则会导致学习信心的下降.因此,在实际的教学中,教师要对解题的方法和思路开展教学,培养学生的解题能力.

