圆锥摆变形记之“双线圆锥摆”

高安强

(临沂华盛教育集团,山东 临沂 276017)

圆锥摆[1]是高中的圆周运动的重要物理模型,圆锥摆的变形较多,例如光滑漏斗内壁圆锥摆、粗糙漏斗内壁圆锥摆、粗糙漏斗外壁圆锥摆、光滑漏斗外壁挂绳圆锥摆、双线圆锥摆等等.很多初学者在学习圆锥摆时,因为圆锥摆及其变形内容繁多,理不清头绪而至烦恼不已,为了解决初学者的这些困扰,下面就对圆锥摆的变形之一——双线圆锥摆进行讨论和总结.

1 双线在两边

如图1,两绳在水平方向的分力之差充当向心力;竖直方向的分力与重力的合力等于零.

例题1 如图1所示,在固定的竖直杆上固定水平杆,二杆垂直,把两根轻绳初端系在水平杆的O、A两点,两绳的末端都系在同一个小球上,小球的质量为m,并且OA=OB=AB=l,现让竖直杆匀速转动,三角形OAB始终在竖直平面内,g为重力加速度,不计空气阻力,则下列说法正确的是( ).

A．当杆转动角速度增加时,OB绳上的拉力变大和AB绳上拉力减小

解析A:对小球受力分析,则

水平方向:

FOBcos60°-FABcos60°=mlcos60°ω2

①

竖直方向:FOBsin60°+FABsin60°=mg

②

由①②两式解得

当杆转动角速度ω增加时,OB绳上的拉力变大和AB绳上拉力减小,故选项A正确;

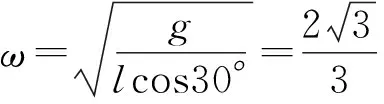
答案:A

2 一线的拉力或一线拉力竖直方向的分力等于摆球的重力

(1)如图2(a)所示,在角速度变化的过程中,因为绳a上的拉力大小不变,大小等于mg;绳b上的拉力充当向心力.

图2 竖直方向拉力或拉力的分力与重力平衡

(2)如图2(b)所示,绳上的拉力大小不变,竖直方向的分力等于重力;水平分力和筒壁的支持力的合力充当向心力;当然筒壁的支持力可能等于零.

例题2如图3所示,竖直圆桶的内壁光滑,绕中心轴做匀速圆周运动,轻绳的另一端系于圆桶上表面圆心,另一端系有一个质量为m的物体,且物块贴着圆桶内表面随圆桶一起转动,轻绳与竖直方向的夹角等于60°,轻绳的长度等于2 m,物块的质量等于1 kg,则( ).

图3 例2题图

A.小物块圆周运动的向心力等于绳子水平方向的分力

B.当ω=10 rad/s时,桶对物块的弹力等于为零

C.当ω=20 rad/s时,绳子的拉力等于20 N

D.当ω=20 rad/s时,筒壁的弹力等于390 N

答案:BC

3 双线在一边

双线圆锥摆如图4(a)、图4(b)、图4(c)所示,三种情况下的临界状态都可以利用离心趋势找出来.

图4 双线在一边

(1)当转轴不转动时,图4(a)、图4(b)、图4(c),三种情况下的小球都会紧靠在转轴上,此时AC绳拉紧而BC绳松弛.小球不离开转轴.

例题3如图5(a)所示,竖直细杆下端固定在位于地面上的水平转盘上,一质量为m的1 kg小球接上长度均为L=2 m不可伸长的两相同的轻质细线a、b,a细线的另一端结在竖直细杆顶点A,细线b的另一端结在杆的中点B,AB长度为l=L.当杆随水平转盘绕竖直中心轴匀速转动时,将带动小球在水平面内做匀速圆周运动,如图5(b).不计空气阻力,重力加速度为g.则( ).

图5 例3题目

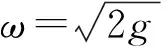
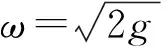
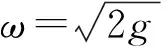
CD:对摆球受力分析如图5(c)所示,列方程

Facos30°+Fbcos30°=mLsin60°ω2

①

Fasin30°=Fbsin30°+mg

②

解得两绳上的拉力等于

Fa=30 N

Fb=10 N

故CD错.答案:A

解答双线圆锥摆的关键还是对摆球受力分析清楚,建立坐标系,在建立坐标系时,要注意两轴的方向,一定要有一个轴指向圆心,这样求出这个轴上的合外力即为向心力,另一个轴上合外力等于零.另外需要明确两个绳子出现和消失拉力的临界点.