轻绳连接体问题的力学规律与求解策略
邓贤彬


以轻绳连接体为背景的物理试题往往能够充分考查物体的受力平衡、牛顿运动定律、运动的合成与分解、动量、能量守恒和功能关系等重要力学知识(如图1所示),以及平行四边形定则、三角函数等数学知识,对同学们的理解能力和数学计算能力的要求较高。要想快速准确地求解轻绳连接体问题,就必须清楚轻绳的力学特性和轻绳连接的两个物体间具有的速度关系、加速度关系、位移关系等。下面归纳整理典型的轻绳连接体问题的求解策略,供大家参考。
一、轻绳之瞬间问题
1.轻绳的定义:没有质量,形变量微小到可以忽略不计的绳子。
2.轻绳的力学特性:轻绳不发生显著形变就能产生弹力,故形变的产生、恢复或改变几乎不需要时间,其弹力可以发生突变。
例1 如图2所示,用两段不可伸长的轻绳悬挂质量为m 的小球,小球处于静止状态时,小球左侧轻绳水平,右侧轻绳与竖直方向间的夹角为θ。以下说法中正确的是( )。
A.剪断水平轻绳的瞬间,小球的加速度为gtan θ
B.剪断水平轻绳的瞬间,小球的加速度为gsin θ
C.剪断倾斜轻绳的瞬间,小球的加速度为g
D.剪断倾斜轻绳的瞬间,小球的加速度为g/sin θ
解析:剪断轻绳的瞬间,其弹力会发生突变。分析此时轻绳的弹力情况需要根据小球以后的运动情况,因为此时轻绳的弹力应为小球以后的运动提供力学条件。
剪断水平轻绳的瞬间,小球开始做圆周运动。小球的受力情况如图3所示,将重力沿绳和垂直于绳方向分解,则T=mgcos θ,F合=mgsin θ,因此小球的加速度a=F合/m =gsin θ,选项A错误,B正确。
剪断倾斜轻绳的瞬间,小球开始做自由落体运动(水平绳无拉力),则小球的加速度a=g,选项C正确,D错误。
答案:BC
例2 如图4所示,质量为M的木块用长为L 的轻绳悬挂于O点,处于静止状态。一质量为m 的子弹以水平速度v0 高速射入木块,子弹没射出木块。不考虑一切阻力,求:
(1)子弹射入木块后,子弹和木块的共同速度v共。
(2)子弹射入木块时轻绳的拉力F。
(3)子弹射入木块后,子弹和木块上升的最大高度H 。
解析:(1)子弹射入木块的时间很短,木块的位置几乎没有变化,子弹和木块就达到共同速度。由子弹和木块组成的系统受轻绳对它竖直向上的拉力和竖直向下的重力,因而在水平方向上受到的合力为零,系统动量守恒,则mv0 = (m + M )v共,解得v共=mv0/m +M 。
(2)子弹射入木块后,由子弹和木块组成的系统开始做圆周运动,系统的受力情况如图5所示,根据运动学公式得F - (m +M )g =(m +M )(v2共/L),解得F=(m +M )g+[m2v20/(m +M )L]。
(3)子弹和木块在向右运动的过程中,因为轻绳的拉力始终不做功,只有重力做功,所以由子弹和木块组成的系统机械能守恒,当系统的速度为零时运动到最高点。根据机械能守恒定律得1/2(m +M )v2共=(m +M )gH ,解得H = [m2/2g(m +M )2]v20。
二、轻绳连接之死结、活结问题
1.“死结”:可理解为把轻绳分成两段,且不可以沿轻绳自由移动的结点。其特点是“死结”让结两侧的两段轻绳变成两根独立的轻绳,因此两段轻绳的张力一般不相等。理论上,一根轻绳可以存在无数个“死结”下的力学平衡状态。
2.“活结”:可理解为把轻绳分成两段,且可以沿轻绳自由移动的结点。其特点是轻绳在结点处发生弯曲,张力方向发生变化,但轻绳仍是同一根绳,“活结”两侧的两段轻绳的张力大小一定相等。一般情况下,处于确定的力学平衡状态下的一根轻绳只能有一个“活结”。
例3 (2020年高考全國Ⅲ卷) 如图6所示,悬挂物体甲的细线拴牢在一不可伸长的轻质细绳上O 点处,细绳的一端固定在墙上A 点,另一端通过光滑定滑轮与物体乙相连。甲、乙两物体的质量相等。系统平衡时,O 点两侧细绳与竖直方向间的夹角分别为α 和β,若α=70°,则β 等于( )
A.45° B.55°
C.60° D.70
解析:本题是轻绳连接体的平衡问题,既有“死结”,又有“活结”。选滑轮处为研究对象,滑轮处为一“活结”,因而滑轮两侧的两段细绳的张力大小相等,且等于物体乙的重力。设甲、乙两物体的质量均为m ,选O 点为研究对象,进行受力分析,如图7所示,因为T1=T2,所以其合力T 在其角平分线上,即∠1= ∠2,根据三力平衡条件可知,TOA 和T 等大反向,则∠1=β。根据几何关系得∠1+ ∠2+α =180°,解得∠1=55°,即β=55°。
答案:B
三、轻绳连接体之系统问题
例4 如图8所示,一根轻绳跨过光滑定滑轮,两端分别连接物体A 和B,物体A 和B 的质量分别为m 和M ,物体A 悬挂在空中,物体B 放于水平地面上。假设轻绳的长度不发生改变,且滑轮的大小可忽略不计。在用水平变力F 拉物体B 沿水平方向向右做匀速直线运动的过程中,( )。
A.物体A 也做匀速直线运动
B.轻绳的拉力始终等于物体A 的重力
C.物体A 做加速运动
D.轻绳对物体A 的拉力逐渐减小
解析:根据运动的合成与分解,将物体B 在初始位置的瞬时速度分解到沿绳方向和垂直于绳方向,如图9所示,则物体A 的速度vA =vB//=vBcos α。物体B 向右匀速运动的过程中,vB 保持不变,轻绳和水平方向间的夹角α 逐渐减小,cos α 逐渐增大,则vA 逐渐增大,即物体A做加速运动,选项A 错误,C正确。对物体A进行受力分析,根据牛顿第二定律得TA -mg=maA ,即TA >mg,选项B 错误。根据数学知识可知,随着α 角的减小,cos α 的值变化减慢,物体A 的速度改变变慢,即aA 减小,故TA 逐渐减小,选项D正确。
答案:CD
問题1:轻绳连接的两物体瞬时速度大小相等吗?
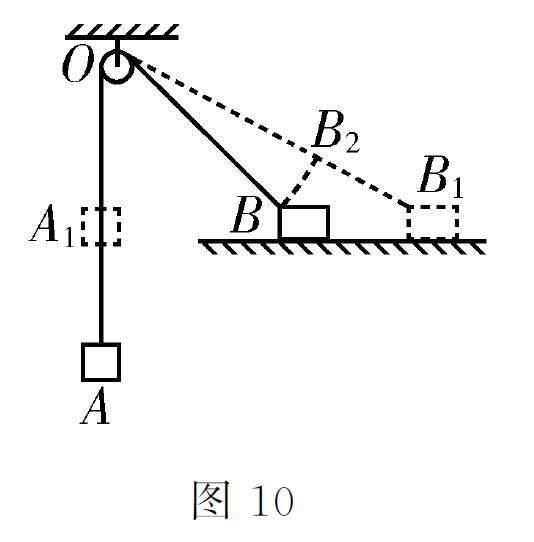
原理分析:为了研究方便,假设物体A和物体B 开始时分别处于位置A 和位置B,令经过一段时间Δt,物体A 和物体B 分别运动到图10 中的A1 和B1 位置,设该段时间内,物体A 和物体B 的位移分别为xA 和xB 。以O 点为圆心,以OB 长为半径画圆弧BB2 交OB1 于B2 点。
位移大小关系:轻绳不能伸长,根据几何关系得xA =xB//,xB >xB//。
原因分析:物体A 和物体B 在相等时间内的位移、速度大小不等的根本原因是物体B 沿垂直于轻绳方向发生了转动。
结论1:轻绳连接的两物体沿绳方向的瞬时速度大小一定相等,即vA//=vB//。
问题2:轻绳连接的两物体沿绳方向的瞬时加速度大小相等吗?
原理分析:物体A 做加速运动,对物体A 应用牛顿第二定律得TA -mg=maA ,其中aA >0。物体B 做匀速直线运动,物体B 受到重力Mg,拉力F,轻绳拉力T,地面摩擦力和支持力作用,处于平衡状态。如图11所示,以水平方向为x轴,竖直方向为y 轴,将轻绳的拉力T 正交分解,则F =f +Tcos α,N +Tsin α=Mg,其中f=μN 。如图12所示,以沿绳方向为x 轴,垂直于绳方向为y 轴,设物体B沿绳方向的加速度为aB//,则(Mg-N)sin α+(F-f)cos α-T=MaB//。联立以上各式解得aB//=0。因此aA ≠aB//。
结论2:轻绳连接的两物体沿绳方向的瞬时加速度大小不一定相等。
问题3:什么条件下轻绳连接的两物体沿绳方向的瞬时加速度大小一定相等?
原理分析:因为轻绳连接的物体沿垂直于绳方向有转动造成了两物体位移、速度大小不等,所以当轻绳连接的两物体沿垂直于绳方向上均没有转动,即两物体都只在沿绳方向上运动时,两物体沿绳方向的位移、瞬时速度、瞬时加速度大小一定相等。
结论3:当轻绳连接的两物体沿垂直于绳方向上没有转动,即两物体都只在沿绳方向上运动时,两物体沿绳方向的瞬时加速度大小和瞬间速度大小一定相等。
练习1:如图13所示,一根轻绳跨过光滑轻质定滑轮,两端分别系在物体A、B 上,物体A的质量M1 =2 kg,物体B 的质量M2 =1 kg,初始状态下物体A 离地高度H =0.5 m。将物体A 与B 由静止开始释放,取重力加速度g=10 m/s2,则物体A 由静止下落0.3 m 时的速度为( )。
A.根号下2 m/s B.3 m/s
C.2 m/s D.1 m/s
答案:A 提示:将物体A 与B 由静止开始释放后,物体A 竖直下落,物体B 竖直上升,均只沿绳方向运动,因此两物体的瞬间加速度大小、运动时间、瞬时速度大小均相等。对由两物体组成的系统应用机械能守恒定律得(M1-M2)gh=1/2(M1+M2)v2,解得v=根号下2 m/s。
问题4:既然物体B 做匀速直线运动,加速度aB =0,为什么物体B 沿绳方向和垂直于绳方向的速度都在发生变化?原理分析:将物体B 在B 点和B1 点的速度vB 、vB1 沿绳方向和垂直于绳方向进行分解,并将vB1 及其分量平移到B 点,如图14所示。从vB//矢量的末端向vB1//矢量的末端引有向线段,

