四省联考解析几何试题的分析与思考
张青松
(云南师范大学实验中学,云南 昆明 650031)
2023年2月,为加强教考衔接,实现平稳过渡,针对2023年云南、吉林、黑龙江、安徽四个省的高考考生使用新课标老高考的情况,教育部教育考试院命制了适应性测试卷,供2023年考生进行适应性考试(下文称“四省联考”).这是数学新高考模式在云南省的首次大规模亮相,意义非凡.本次试题以《普通高中数学课程标准(2017年版2020年修订)》为依据,考查了学生的关键能力,突出思维品质与创新精神;注重学用结合,创设真实灵活情境;命题设问更具开放性与探究性.整份试卷充分发挥高考“立德树人、服务选才、引导教学”的核心功能,对后期的复习备考将起到积极而深远的引导作用.
1 试题结构分析
解析几何类试题在四省联考试卷中一共有4道,其中单选题、多选题、填空题和解答题各有一道,合计27分,占整张试卷的分值比例为18%.这几道试题涉及的知识点主要有圆的参数方程、椭圆的几何性质、双曲线的标准方程、圆与抛物线的位置关系、直线与双曲线的位置关系,以及解析几何与三次函数、三角函数的融合.试题结构明了,重在检测考生的四基、四能的发展水平.具体分布见表1.

表1 四省联考解析几何试题考查目标分析
2 试题解法分析
试题1 已知点A,B,C为椭圆D的三个顶点,若△ABC是正三角形,则D的离心率是( ).


图1 长轴端点为三角形顶点 图2 短轴端点为三角形顶点
评析本题是一个椭圆离心率求解的问题,可视为人教A版选修一139页第10题的一个变式,试题如下:
已知等边三角形的一个顶点位于原点,另外两个顶点在抛物线y2=2px(p>0)上,求这个等边三角形的边长.
对于四省联考的这道试题,题目给出的条件是需要我们分类讨论研究问题的,题干给出了三个顶点,但没有明确是哪些顶点,这里就可以分为“有两个长轴顶点”和“有两个短轴顶点”这两种情况进行分析.除去考虑分类讨论这点之外,本题难度不大,因为给出的是顶点的关系,自然可以很容易找到椭圆中a和b的关系.

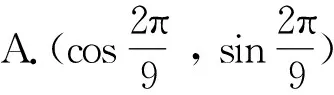



图3 动点运动图
设第ts时,P,Q两点重合,由动点运动路径的长度关系列等式如下:


故选ABD.

即f(k+3)=f(k),

试题3若P,Q分别是抛物线x2=y与圆(x-3)2+y2=1上的点,则|PQ|的最小值为____.
解析如图4,设该圆的圆心为C,由三角不等式可知|PQ|≥|PC|-|CQ|(当P,Q,C三点共线时取等,点Q在点P,C之间),其中|CQ|为半径,即|CQ| =1,所以|PQ|≥|PC|-1.问题转化为求|PC|的最小值.
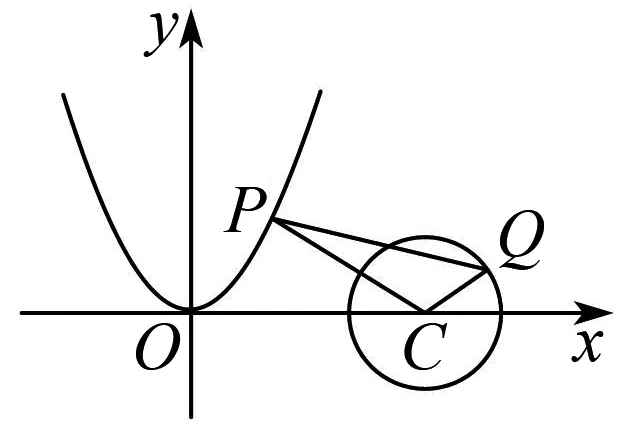
图4 试题3图

设f(x)=x4+x2-6x+9,则f′(x)=4x3+2x-6=2(2x3+x-3)=2(x-1)(2x2+2x+3).
又f″(x)=12x2+2>0,
所以f′(x)在R上单调递增.
当x∈(-∞, 1)时,f′(x)<0,f(x)单调递减;当x∈(1, +∞)时,f′(x)>0,f(x)单调递增.


解法2 (几何法计算最值)当CP与点P处切线垂直时,|PC|取到最小值.
对y=x2求导可得y′=2x.


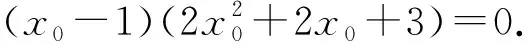
可得x0=1,所以P(1 , 1).

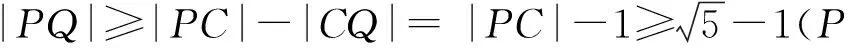

评析本题是一个双动点最值的求解问题,背景是抛物线和圆,可视为2014年福建高考理科数学第9题的一个变式,试题如下:

对于四省联考的这道试题,首先P,Q两点是不相关的两个变量,处理的思路必然是“固定一个,变化一个”.这里可先认为点P是定点,那么|PQ|的最小值就变成了“圆上动点到定点的距离最值”,这种问题就可以利用三角不等式转化为点P到圆心的距离求解,该距离减去半径就是距离最小值了.接下来问题就转化为点P到圆心的距离最小值,此时问题就转化为“抛物线上动点P到定点的距离最值”.
本文提供了两种解题方法,一种比较直接,就是纯代数方式处理,即设出点P的坐标,之后表达线段的长度并求解最值.线段长度表达式的核心部分是一个四次函数,求导后为三次函数,考生需要进行因式分解来判断导函数正负进而求解最值.而如何因式分解是本题的一个难点,可以教学生如下思考:由2x3+x-3的系数和为零,可知该三次多项式必然存在因式x-1,从而可将-3拆成-1和-2,即2x3-2+x-1,再根据试卷第22题给出的立方差公式得2(x-1)(x2+x+1)+(x-1),到此便可实现因式分解.对于系数和不为零的整系数多项式因式分解,读者可参考以下定理.

定理的证明,在一般的高等代数教材中均可找到,在此省略.
第二种思路则是利用几何关系,若定点与P连线垂直于在点P处的切线,对应的距离就是最小的,这里需要一定的观察能力或者平常学习的积累.这种方法虽然没有求导,但是也需要求解一个三次方程,总之此题是绕不过三次函数的处理的.

(1)求C的方程;
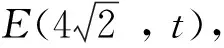
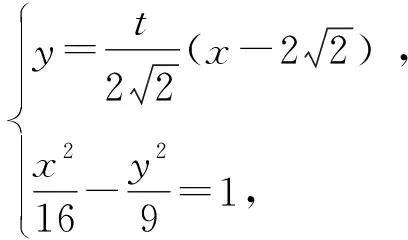

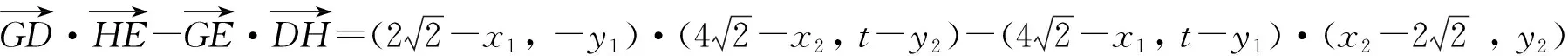

评析本题可视为2008年安徽高考卷第22题的一个变式.解题的核心思想是将线段比转化为共线向量处理,类似的思路出现于2021年全国Ⅰ卷的解析几何题,蕴含了命题人对命制试题的理解,具有很强的指导性.用向量的数量积运算,能很快剥离出运算式的韦达定理的结构,整合分类讨论.不足之处是计算量较大.
3 高考复习启示
3.1 夯实基础,提升思维
从本次四省联考的解析几何试题来看,试题倾向于考查考生的逻辑推理能力,有着“送分题少、中档题目占比大、难题梯度明显”的特点,而且在中档题目上强调更加灵活地应用所学知识和相应的数学技能.在复习备考时,首先让学生牢固掌握直线、圆和圆锥曲线的相关概念,熟悉基本图形和几何性质,建构知识体系;其次,让学生深化理解通性通法,教学时不宜过度追求一题多解,应重点关注如何审题,怎样应用所学知识处理新问题;最后,以解析几何为例,这份试卷的计算量较大,并且逻辑推理的要求也较高,因此我们在平常教学时,要同时抓学生的计算能力和数学思维.
3.2 回归课本,研究真题
有很多高考试题来自于教材例题或习题的改编,教材是最好的备考素材.教学时立足习题,尤其让学生把那些“看上去没有思路”的题多做几遍,争取能独立解决.此外,教材上的“阅读与思考”“探究与发现”等栏目也非常重要,让学生认真阅读并思考这些内容,培养他们阅读习惯的同时提升学习能力.
高考真题凝结着命题专家的智慧,是考查基础知识、基本技能和基本思想方法的载体[1],既有示范性,又有权威性.从本文的分析看,高考试题具有很强的传承性,研究往年真题,挖掘背后的命题规律,对于复习备考具有重要的指导意义.

