一道诊断性试题的多解探究及溯源推广

刘 艳

(四川省名山中学,四川 雅安 625100)

高考数学对圆锥曲线的考查一直体现基础与综合并存,应用与创新充分衔接的特点,每道圆锥曲线题都值得我们去深入探究和思考,由此引发的很多高考改编题也耐人寻味.本文以一道诊断性试题为例,对此题展开多解探究,并对问题进行溯源和推广,得到了一般性结论,最后对解析几何教学中如何提升学生核心素养方面进行反思,以期能在教学实践中更好地推进新高考改革.

1 题目呈现

(1)求椭圆C的标准方程;

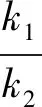
2 多解探究

2.1 第(1)问解析

2.2 第(2)问解析

2.2.1根与韦达合理搭桥,慧眼识金巧消元

解法1 由题意直线l的斜率不为零,故设其方程为x=my+4.

(3m2+4)y2+24my+36=0.

①

由Δ>0,得m2>4.

设A(x1,y1),B(x2,y2),则由韦达定理有

易知F(1,0),所以

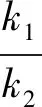
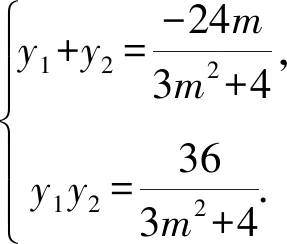
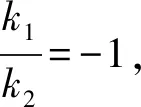
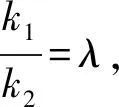
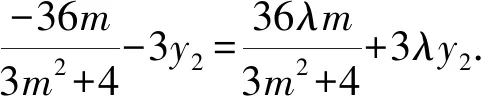
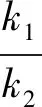
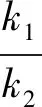
解法5由题意直线l的斜率存在且不为零,故设其方程为y=k(x-4).

(3+4k2)x2-32k2x+64k2-12=0.

又F(1,0),所以

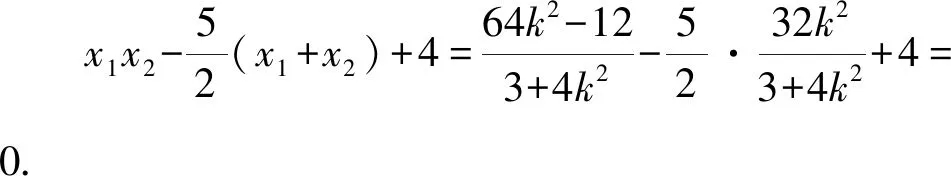
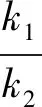
2.2.2数形结合巧移图形,齐次转化构斜率

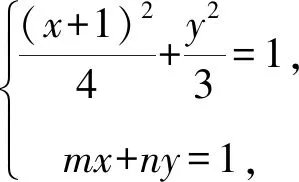
3x2+6x(mx+ny)+4y2-9(mx+ny)2=0.

整理,得(3+6m-9m2)x2+(6n-18mn)xy+(4-9n2)y2=0.

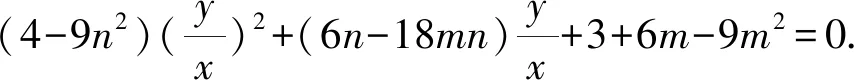
2.2.3活用条件结论齐构造,高屋建瓴妙解题

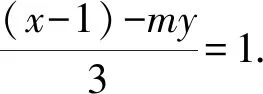
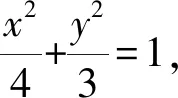
整理,得12(x-1)2+(12-3m2)y2=0.

两边同时除以(x-1)(x≠1),得

3 溯源推广

3.1 试题溯源

近年来,很多高考解析几何题均以高等几何中的有关概念和性质为指导,本题追溯到高等几何中的极点、极线内容,下面给出相关概念和定理.

定义1点P在圆锥曲线外,过点P作曲线的两条割线,分别交曲线于A,B和C,D,设AC∩BD=X,AD∩BC=Y,则直线XY为点P的极线(如图1).

图1 定义1图 图2 定义2图

定义2点P在圆锥曲线内,过点P作两条直线,分别交曲线于A,B和C,D,设AC∩BD=X,AD∩BC=Y,则直线XY为点P的极线如图2所示.

定理1 (配极原则) 如果点P的极线通过点Q,则点Q的极线也通过点P.

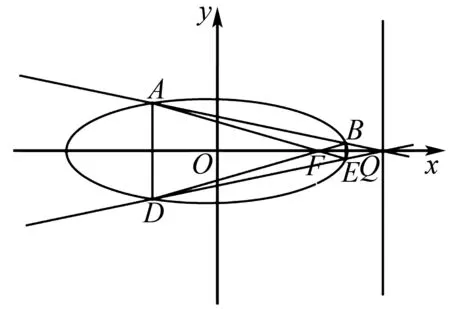
图3 定义1图

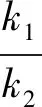
3.2 推广探究

通过以上极点极线知识分析,进一步推广得到如下结论:

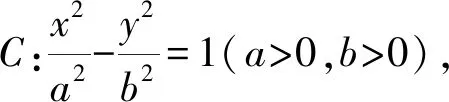
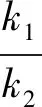
4 解题反思

4.1 多解探究,积累通性通法

通过一题多解,引导学生积累解决一类问题的通性通法,达到“解一题,会一法,通一类”的学习目的.本题中第(2)问很多同学知道用韦达定理来解决问题,但却无法整体找到两根之和与两根之积之间的关系,桥梁建立不起来,最后无计可施只能到韦达定理这一步为止了.但如果想到借助求根公式与韦达定理同时搭桥,本题也能迎刃而解.如果能再借助图形分析猜想直线AF,BF的倾斜角互补,再验证一下它们的斜率之和,本题也能顺利解决.所以,在圆锥曲线解题中,韦达定理虽然经常用,但很多学生只通其一不通其二,在遇到这种所谓的非对称结构运算问题时,学生如果没有经验,考试时是难以过关的.而齐次构造是处理斜率问题的通性通法,如果学生能灵活处理好条件结论中的代数关系,此题也能很好地解决[2].

4.2 把握本质,重视思想运用

素养的培养更重要的是要注重数学思维的培养,领悟知识背后的本质,重视知识背后的数学思想的渗透.高中解析几何内容兼具几何与代数双重特性,在教学时应不拘泥于套路形式,应突出和把握问题的本质.比如本题中韦达定理学生学得太死了,导致学生感觉用韦达定理解决不了这个问题,其实本题运用的本质是消元和转化思想,如何消元,如何将已知转化出来为我所用或者将未知转化为已知,处理方法有很多种,思路打开了,问题也就能解决了.