圆锥曲线的弦对顶点张直角的一个定值性质

刘才华

(山东省泰安市宁阳第一中学,山东 泰安 271400)

已知抛物线C的方程为y2=2px(p>0),焦点为F.已知点P在C上,且点P到点F的距离比它到y轴的距离大1.

(1)试求出抛物线C的方程;

这是一道高三年级模拟试题,我们通过探究,对试题作进一步的推广,得到圆锥曲线的弦对顶点张直角的一个定值性质,性质的证明需用到如下引理:

引理1 设直线l与抛物线y2=2px(p>0)相交于A,B两点,则OM⊥ON(O为坐标原点)的充要条件是直线l过定点(2p,0)[1].

对于抛物线,我们有如下命题:

证明由题意及引理1知直线MN过定点E(2p,0),设过点E的直线方程为x=my+2p,交抛物线于M(x1,y1),N(x2,y2).

y2-2pmy-4p2=0.

则y1y2=-4p2.

y2-2pmy-p2=0.

则y3+y4=2pm,y3y4=-p2.

=2p(1+m2).

命题1得证.

对于椭圆,我们有如下命题:

(a2+b2)2(b2m2+a2)y2+2mab2(a4-b4)y-4a4b4=0.

过点F(c,0)的直线方程为x=my+c,交椭圆于A(x3,y3),B(x4,y4).

(b2m2+a2)y2+2cmb2y-b4=0.

对于双曲线,我们有如下命题:

(a2+b2)2(b2m2-a2)y2+2mab2(a4-b4)y-4a4b4=0.

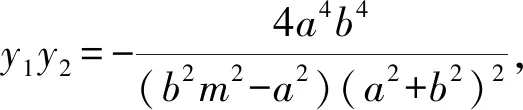
过点F(c,0)的直线方程为x=my+c,交双曲线于A(x3,y3),B(x4,y4).

(b2m2-a2)y2+2cmb2y+b4=0.