谈杨辉三角及其蕴藏的数列问题

张利河

摘要：“杨辉三角”是中国悠久数学文化的代表之一.其蕴含着丰富的数学规律，其中，从杨辉三角的斜看或横看，各列各行的数字排列规律代表着不同数列，这些独自看来互不相关的不同数列，不同的通项公式以及求各公式，却在杨辉三角中直观地显而易见地得到答案.将这些数列与杨辉三角以及组合数之间的特性放在一起学习，从中寻找彼此间密切的联系，以拓宽学生数学视野，构建完整知识体系，达到融会贯通事半功倍的效果.

关键词：杨辉三角；二项式系数；数列问题

中国古代数学曾经有自己光辉灿烂的篇章，“杨辉三角”便是这灿烂的篇章中的光辉一页，是中国悠久数学文化的代表之一.杨辉三角看似简单的数字排列，却蕴含着众多精彩绝伦的数学结论，以及博大精深的数学文化.杨辉三角将二项式系数用直观图形表示出来，能将很多繁杂的数学问题得到简便解决.

杨辉三角的结构性质：

（1） 杨辉三角每一行左右两端的数相等，即Crn=Cn-rn.

（2） 杨辉三角每一行除头尾两数都是1外，其余的各数都等于其“肩上”相邻两数之和，即Crn+Cr-1n=Crn+1.

（3） 杨辉三角第n行为（a+b）n展开式的二项式系数，第n行第m列数为Cm-1n.

在杨辉三角的结构性质中，从杨辉三角的斜看或横看，各列各行的数字排列规律代表着不同数列，这些独自看来互不相关的不同数列，不同的通项公式以及求各公式，却在杨辉三角中直观地显而易见地得到答案.下面谈谈几个不同的数列是怎样不约而同地出现在杨辉三角当中.

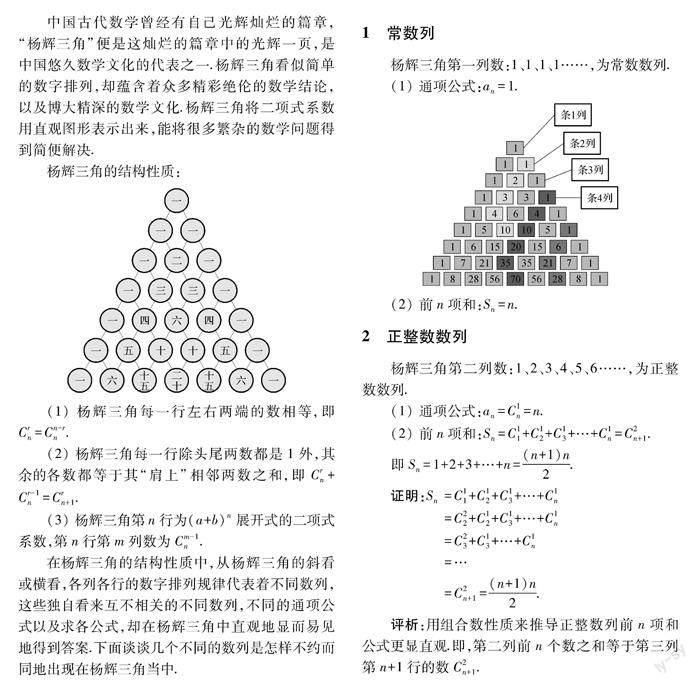
1常数列

杨辉三角第一列数：1、1、1、1……，为常数数列.

（1） 通项公式：an=1.

（2） 前n项和：Sn=n.

2正整数数列

杨辉三角第二列数：1、2、3、4、5、6……，为正整数数列.

（1） 通項公式：an=C1n=n.

（2） 前n项和：Sn=C11+C12+C13+…+C1n=C2n+1.

即Sn=1+2+3+…+n=（n+1）n2.

证明：Sn=C11+C12+C13+…+C1n

=C22+C12+C13+…+C1n

=C23+C13+…+C1n

=…

=C2n+1=（n+1）n2.

评析：用组合数性质来推导正整数列前n项和公式更显直观.即，第二列前n个数之和等于第三列第n+1行的数C2n+1.

3三角形数

杨辉三角第三列数：1、3、6、10、15、21，为三角形数，三角形数特点就是这些数能够组成各个等边三角形的点的数目，所以将这样的数称为三角形数.

（1） 3.1通项公式：an=C2n+1=（n+1）n2.

即，三角形数第n个数第三列第n+1行的数C2n+1.

（2） 前n项和：Sn=C22+C23+C24+C25+…+C2n+1=C3n+2=（n+2）（n+1）n6.

用数列“累加法”可推导出该数列的通项公式，若用杨辉三角可直观看出该通项公式就是第二列的前n个数之和，即，C11+C12+C13+…+C1n=C2n+1.求该数列的前n项和若用数列知识求解显得繁杂，可在杨辉在杨辉三角上其结论也是一目了然.即该数列的前n项和就是第四列的第n个数C3n+2.

4四面体数

杨辉三角第四列数：1、4、10、20、35、56……，为四面体数，四面体数就是构成一个四面体所需要的点的数目，四面体数每层为三角形数.即，四面体数列第n个的数an为杨辉三角第4列数第为n+2行的数C3n+2，

（1） 通项公式：an=C3n+2=（n+2）（n+1）n6，

（2） 前n项和：Sn=C33+C34+C35+C36+…+C3n+2=C4n+3=（n+3）（n+2）（n+1）n4×3×2.

评析：三面体数1、4、10、20、35、56…，该数列的前n项和若用数列知识求解更显得繁杂，可在杨辉在杨辉三角上其结论也是一目了然.即该数列的前n项和就是第5列的第n个数C4n+3.

由上述可知，杨辉三角的前四列数分别表示四个不同的数列，第一列数是通项为1的常数列；第二列数为正整数数列，且第一列数的前n项和为该数列通项公式；第三列数为三角形数，且第二列数的前n项和为该数列通项公式；第四列数为四面体数，且第三列数的前n项和为第四列数的通项公式.四个不同的数列在杨辉三角中可看出有着密切联系，那就是它们前一列数的前n项和就是下一数列的通项公式.这些不同的数列，用同一个组合数式子：Crr+Crr+1+Crr+2+…+Crr+n=Cr+1r+n+1，就可非常直观地表明它们的通项公式和前n项和公式联系.假如从斜看杨辉三角已经展其的神奇魅力.那么从横看杨辉三角一样有其独特风采.

5杨辉三角第n行的数列有下列特点

（1） 第n行的数字之和为2n即，C0n+C1n+C2n+C3n+…+Cnn=2n.

（2） 第n行所有数字的平方和恰好是第2n行的中间一项的数字，即（C0n）2+（C1n）2+…+（Cnn）2=Cn2n.

证明：

（1） 因为（1+x）n=C0n+C1nx+C2nx2+…+Cnnxn

令x=1，可得C0n+C1n+C2n+C3n+…+Cnn=2n.

（2） 因为（1+x）2n=（1+x）n（1+x）n=

（C0n+C1nx+C2nx2+…+Cnnxn）·（Cnnxn+Cn-1nxn-1+Cn-2nxn-2+…+C0n），

则由xr项和xn-r项相乘即可得到xn这一项的系数为：

（C0n）2+（C1n）2+…+（Cnn）2=Cn2n，

而Cn2n是二项式（1+x）2n的展开式中第n+1项的二项式系数（即xn的系数），

故（C0n）2+（C1n）2+…+（Cnn）2=Cn2n.

6杨辉三角揭示了11为底的幂的值

11n=（10+1）n=C0n10n+C1n10n-1+C2n10n-2+C3510n-3+…+Cnn，觀察杨辉三角每一行数字特点可直观看出，将杨辉三角每一行的数字“紧密”地排成一排构成一个整数，这个数就是11n的值，如果各行当中出现大于等于10的时候，将十位数加到它左侧数字上留下个位数，依此类推，如果出现了大于等于100的数的时候，同样进位处理即可.这也是杨辉三角的漂亮之处.如：

例：如图所示，下列关于杨辉三角的说法中正确的有（）

A. C22+C23+C24+…+C211=220.

B. 1+C16+C27+C38=C39.

C. 将杨辉三角每一行中所有的1去掉，留下新数列2，3，3，4，6，4，5，10，10，5，…，则该数列的前57项和T55=4 150.

D. 由“11=111，121=112=，1331=113=”猜想：117=19 487 171.

解：（1） 因为C22+C23+C24+…+C211=C312=220，故A正确.

（2） 因为1+C16+C27+C38=C55+C56+C57+C58=C69=84，故B正确.

（3） 杨辉三角去掉1之后，留下的各行数个数成首项为1的等差数列，除去第一行，剩下的每一行剩下的项数分别为1，2，3…，构成一个等差数列，令项数之和为n（n+1）2=55，n的最大整数为10，即刚好为杨辉三角第11行，因为杨辉三角前11行数字之和S11=1+21+22+23+…+211=212-1，这11行中共去掉了23个1为T55，

T55=212-1-23=4 072，故C错误.

（4） 因为杨辉三角第7行数为1、7、21、35、35、21、7、1，将它们“挤压”到一起.出现两位数的时候将十位数加到它左侧数字上可得，117=19 487 171，所以D正确.故选：ABD.

7斐波那契数列

将杨辉三角各向左对齐，换一角度“斜”向看，斜线和依次为：1、1、2、3、5、8、13、21、34……这些数构成斐波那契数列.

a1=1，a2=1，a3=2，an=an－1+an－2（n≥3）即，

8莱布尼茨三角形

莱布尼茨三角形是第一行为1，第二行为两个12，两腰的数字依次是其行行数的倒数，从第二行开始，下一行相邻两个数的和恰好等于上面的数.

评析：根据莱布尼茨三角形的数字排列秩序，可发现其与杨辉三角形也有着的密切联系.观察莱布尼茨三角形的数字排列规律，可发现莱布尼茨三角形与杨辉三角形也有着的密切联系.将莱布尼茨三角第n行所有数字提出公因数1n+1后，其留下的三角形上各数恰好为将杨辉三角各数的倒数，即1（n+1）Crn+1（n+1）Cr+1n=1nCrn-1.

杨辉三角，这些表面看上去只是一堆排列整齐的数字，它可是一个数学的宝藏.杨辉三角中所蕴藏了很多优美的结论，让世界各国数学家而着迷.印度数学家称它为“须弥山之梯”.在伊朗，它是“海亚姆三角”.各个不同时期数学家发现的一些数学规律在杨辉三角中悄然“融会”，并将这些抽象的数学规律在杨辉三角中轻松“贯通”.比如上述例举一系列重要数列同时在杨辉三角中找到身影.杨辉三角外形之整齐对称美，更有内在美，这是一种有文化有内含有韵味的气质美，杨辉三角作为我国灿烂悠久的历史文化，其魅力不仅在过去而且在当今依然不减，杨辉三角还有什么不为人知的神奇的性质，有待所有数学爱好者继续探索和发现.