杨辉三角的“前世今生”
黄 雨 苏里阳
(1.淮南第二中学 2.淮南市教研室)
杨辉三角是我国数学史上一颗璀璨的明珠,是我国为数不多的居于世界前列的数学成就,它的发现比欧洲的帕斯卡三角形早了近600年,是非常值得中华民族自豪的.而今天的数学学习者中大多数人已经不知道杨辉三角的发现者是谁,对杨辉三角的知识背景知之甚少.人教A版教材选择性必修三第39页有个专题是《杨辉三角的性质及应用》,但由于教师和学生的不重视,忽视对中国传统文化的继承和发扬,导致最近的一次数学测试中,命题者问杨辉三角是谁发现的,92.8%的人凭惯性思维选择是杨辉,一个5分的选择题,平均分仅有0.36分.故笔者认为有必要在这里探讨一下杨辉三角的知识背景、性质及应用.
一、争论
学术界和网络上都存在着对杨辉三角发现者的争论,有人认为是杨辉、有人认为是贾宪、还有人认为要早于贾宪.
首先我们要明白一个规则:史学家研究历史通常来自两个方面,一个是文字,一个是文物.既无文字记载,又无文物印证,仅凭猜测和想象是无效的.
杨辉三角原本叫“开方作法本源”图(如图1(1)),由元代数学家朱世杰推广成“古法七乘方图”(如图1(2)),近代数学家华罗庚等人称其为杨辉三角.南宋数学家杨辉在《详解九章算法》中曾记载“出释锁算书,贾宪用此术”.此段话记载在明《永乐大典》中,因为八国联军的入侵,《永乐大典》所抄录杨辉原著被掠走,今存英国剑桥大学博物馆,国内仅存杨氏专著数十页.
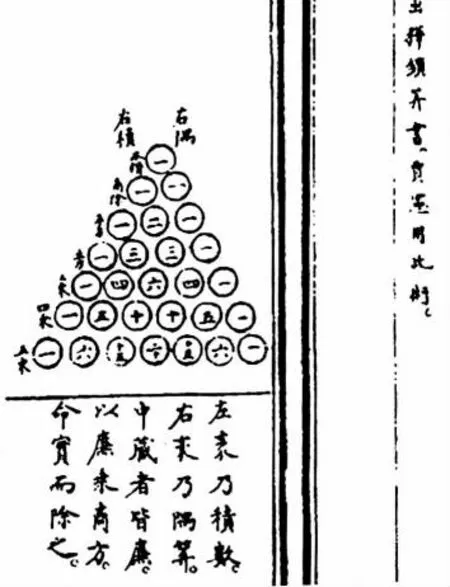
图1(1)
贾宪,北宋人,身世所知甚少,有文字记载:近世司天算,师从楚衍,运算亦妙,有书传于世.贾宪的学术专著久佚,幸赖南宋杨辉所著算法较多,保存了很多贾宪的方法,如释锁开方与增乘开方.贾宪开方作法本源图,恰是二项六次式的展开式系数表,图下有五句话说明,“左袤乃积数,右袤乃隅算.中藏者皆廉,以廉乘商方,命实而除之.”大体说,贾宪是用这张表所示系数借以开方,所以他名此表为“开方作法本源”,这些名词在释锁开方中也都出现过.
从上述文献中我们可以发现,现有史料中有明确记载的就是贾宪首先使用了“开方作法本源”,并为之命名.
二、性质
杨辉三角有很多有趣的性质,笔者就常见并重要的性质结合组合数的运算进行分析.其中m,n∈N.
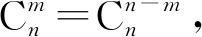
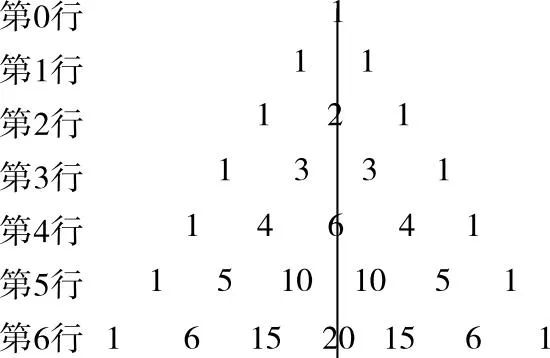
图2
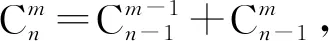

图3
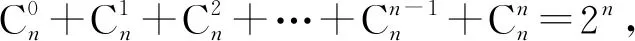

图4
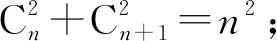
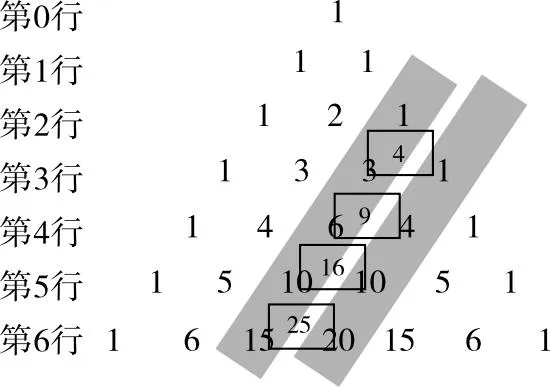
图5
5.将杨辉三角左对齐,对角线求和得到斐波那契数列,如图6.
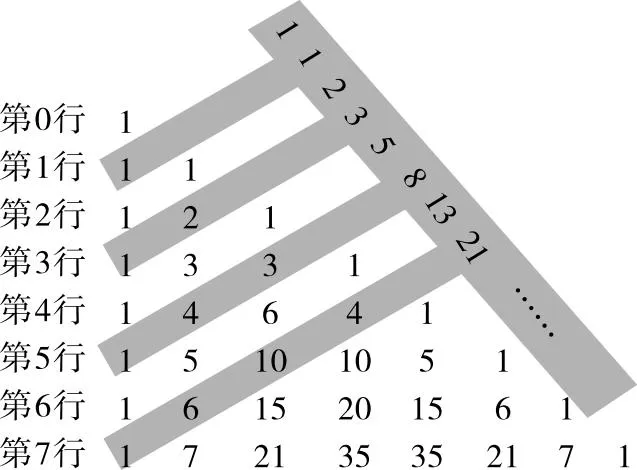
图6
斐波那契(Fibonacci,约1175—1250),中世纪意大利数学家,是西方第一个研究斐波那契数的人,并将现代书写数和乘数的位值表示法系统引入欧洲.

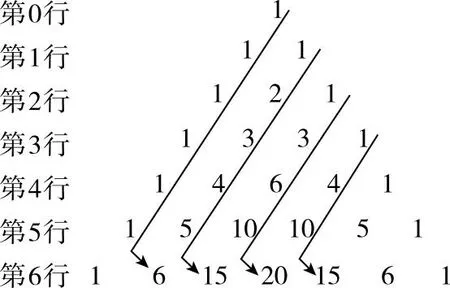
图7
7.将杨辉三角中的奇数涂黑,得到谢尔宾斯基三角形,如图8.

图8
8.除了第二层自然数列包含了素数以外,其他部分的数字都完美避开了素数,如图9.

图9
9.可以被特定数整除的数字形成了奇妙的分形结构.如图10(1)—(4),分别是能被2,3,4,5整除的数涂黑后的分形结构图.

图10(1)


图11
三、应用
【例1】如图12,在杨辉三角中,斜线l的上方从1按箭头所示方向可以构成一个“锯齿形”数列:1,3,3,4,6,5,10,…,则这个数列的第19项为

图12
( )
A.55 B.110 C.58 D.220

【点评】本题利用了杨辉三角的第4条性质,斜向第三列为三角形数列,易解.
【例2】杨辉三角中的第5行除去两端数字1以外,均能被5整除,则具有类似性质的行是
( )
A.第6行 B.第7行
C.第8行 D.第9行
【解析】由题意,第6行为:1 6 15 20 15 6 1,第7行为:1 7 21 35 35 21 7 1,
故第7行除去两端数字1以外,均能被7整除,故选B.
【点评】本题利用了杨辉三角的第9条性质,易解.
【例3】以下数表源于“杨辉三角”的原理,该表由若干行数字组成,从第二行起,每一行的数字均等于其肩上两数之和,表中的最后一行仅有一个数为
( )
1 2 3 4 5 …… 2013 2014 2015 2016
3 5 7 9 ………… 4027 4029 4031
8 12 16 ……………… 8059 8060
20 28 …………………… 16116
A.2017×22015B.2017×22014
C.2016×22015D.2016×22014
【解析】由题意,共有2 016行,第1行的第1个数字为(1+1)×2-1,第2行的第1个数字为(2+1)×20,第3行的第1个数字为(3+1)×21,…,第2 016行的第1个数字为(2016+1)×22014,故选B.
【点评】类比得到杨辉三角性质的过程,进行归纳推理,得出结果.
【例4】如图13所示是竖直平面内的一个“通道游戏”,图中竖直线段和斜线段都表示通道,并且在交点处相遇.若有一条竖直的线段为第一层,第二条竖直线段为第二层,以此类推.现有一颗小球从第一层的通道向下运动,在通道的交叉处,小球可以落入左右两个通道中的任意一个,记小球落入第n层的第m个竖直通道(从左往右计)的不同路径数为A(n,m)(m,n∈N*).
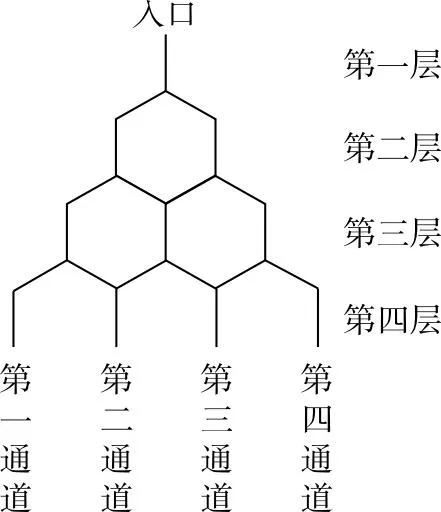
图13
(1)求A(3,2),A(3,3),A(4,3)的值.
(2)猜想A(n,m)的表达式(不必证明),并求不等式A(10,m)≤84的解集.
【解析】(1)A(3,2)=2,A(3,3)=1,A(4,3)=3;
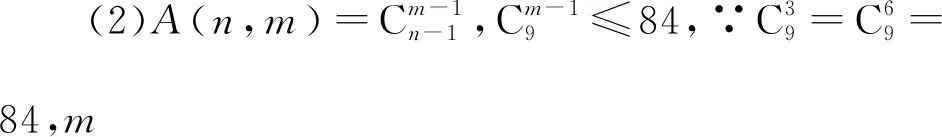
【点评】利用杨辉三角中的数与二项式系数的关系.
【例5】如图14,把杨辉三角左对齐排列,将同一条斜线上的数字求和,会得到一个数列{an},其中a1=1,a2=1,a3=2,a4=3,…设数列{an}的前n项和为Sn.
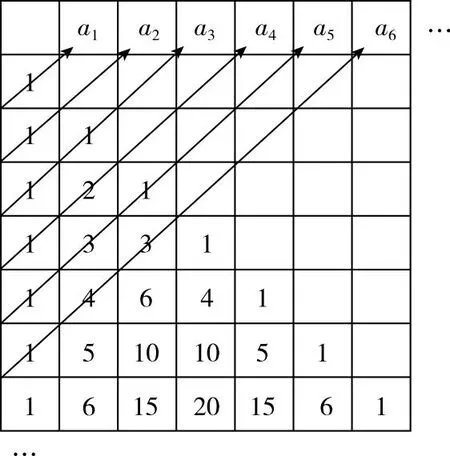
图14
(1)求a8的值,并写出an,an+1,an+2满足的递推关系式(不用证明);
(2)记a2022=m,用m表示S2020.
【解析】(1)由杨辉三角的性质可知,此数列为斐波那契数列.
故a8=21,an+2=an+1+an.
(2)因为a3=a2+a1,
a4=a3+a2,
a5=a4+a3,
……
a2021=a2020+a2019,
a2022=a2021+a2020,
相加得a2022-a2=S2020,
所以S2020=m-1.
【点评】本题利用杨辉三角的第5条性质,构成斐波那契数列.
杨辉三角还有很多有趣的性质,读者可以查阅资料,发掘更多有趣的内容.杨辉三角的应用也非常广泛,在信息技术、概率统计等领域都有其身影,希望读者能继承我国数学传统文化,感悟数学价值,并发扬光大,让世人知晓.

