定比分点解答题,巧用坐标不联立
——谈“定比点差法”在解析几何解答题中的妙用
唐 洵
(福建省福清第三中学)
近年高考圆锥曲线的解答题中,有一类定比分点的问题,既可以通过联立直线与圆锥曲线得到答案,也可以使用“定比点差法”进行求解;相比联立而言,“定比点差法”侧重于点坐标的转化与应用,具有计算量小、目的性强的优点,根据此方法可以解决与定点、定线、定值、定比相关的四类问题.
1.预备知识讲解——兵马未动,粮草先行
(1)一个定义:
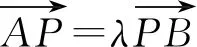
说明:①若λ>0,则点P在线段AB上(不含端点位置);特别地,若λ=1,则点P为线段AB的中点;②若λ<-1,则点P在线段AB的延长线上;③若-1<λ<0,则点P在线段AB的反向延长线上;其中①中的点P为线段AB的内定比分点,②③中的点P为线段AB的外定比分点.
(2)一个结论:
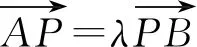
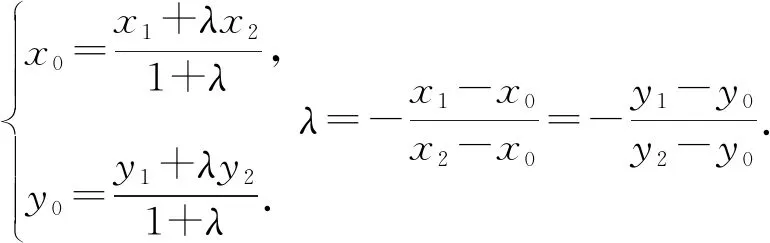
(3)一种方法:
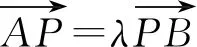
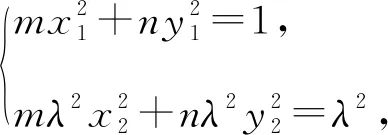
两式相减可得,m(x1+λx2)(x1-λx2)+n(y1+λy2)(y1-λy2)=1-λ2,
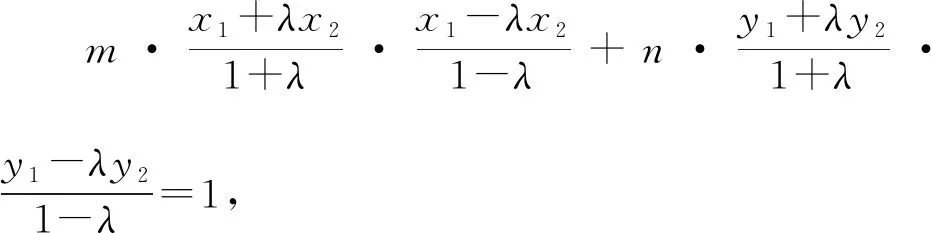
形如这样的方法叫作“定比点差法”,它可以看作是点差法的延伸,无论是椭圆、双曲线还是抛物线中,若遇到定比分点问题,都可以考虑使用该法进行解题.
2.高考真题引航——脚踏实地,付诸实践
下面先让我们来看看“定比点差法”在近两年高考解析几何解答题中的应用.
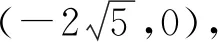
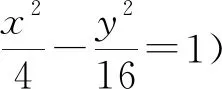
(2)记C的左、右顶点分别为A1,A2,过点(-4,0)的直线与C的左支交于M,N两点,M在第二象限,直线MA1与NA2交于点P,证明:点P在定直线上.
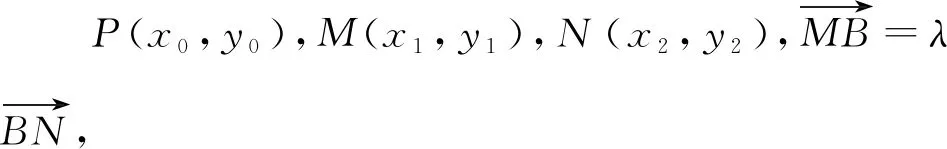
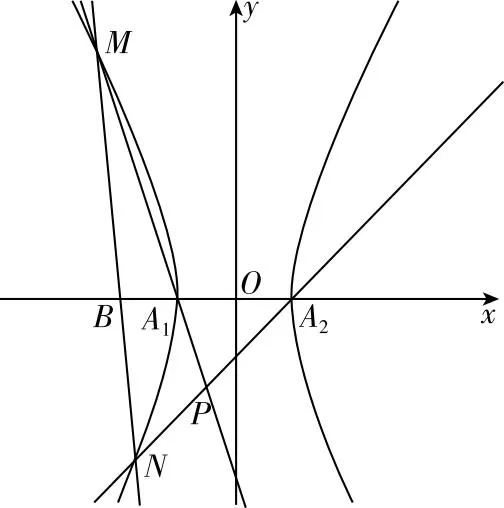
图1 2023新高考Ⅱ卷21题配图
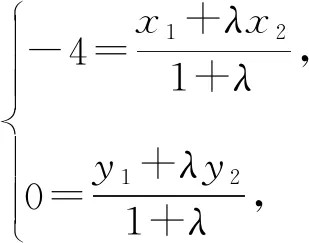
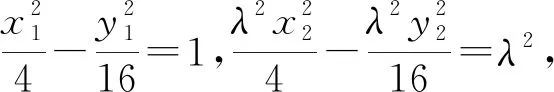
整理得x1-λx2=λ-1,
而x1+λx2=-4-4λ,
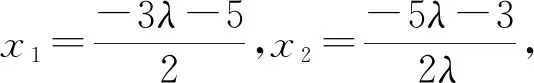
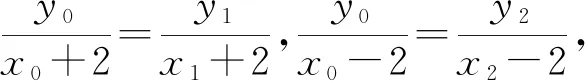

故点P在直线x=-1上.
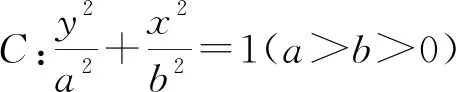
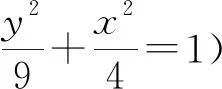
(2)过点(-2,3)的直线交C于P,Q两点,直线AP,AQ与y轴的交点分别为M,N,证明:线段MN的中点为定点.
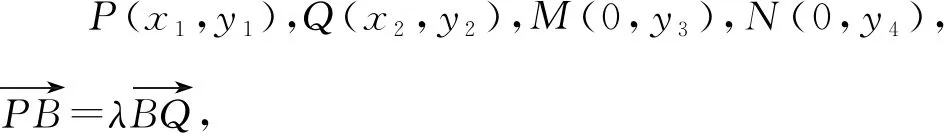
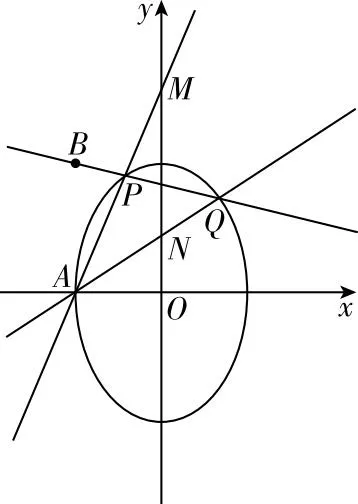
图2 2023全国乙卷理20文21题配图
由①可得,x1+2=-λ(x2+2) ③.
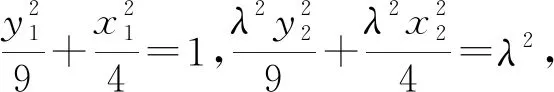


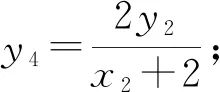
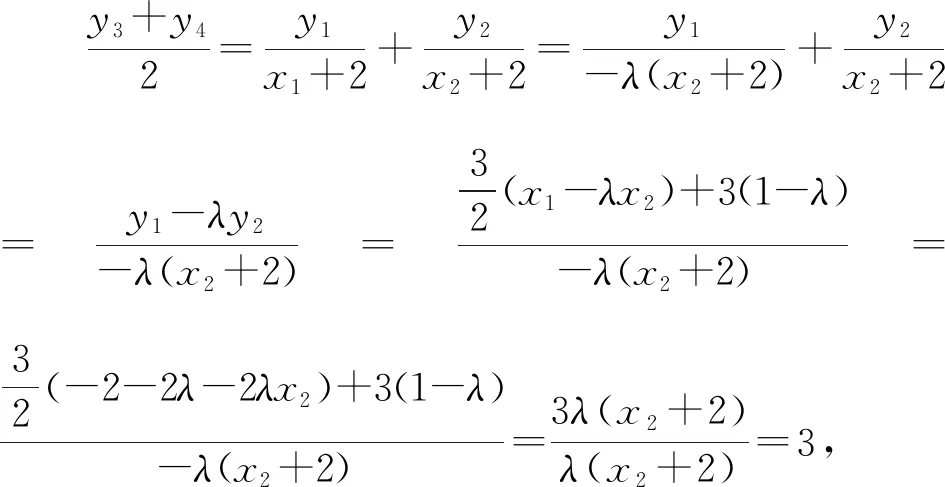
故线段MN的中点坐标为(0,3).
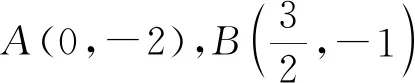
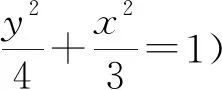


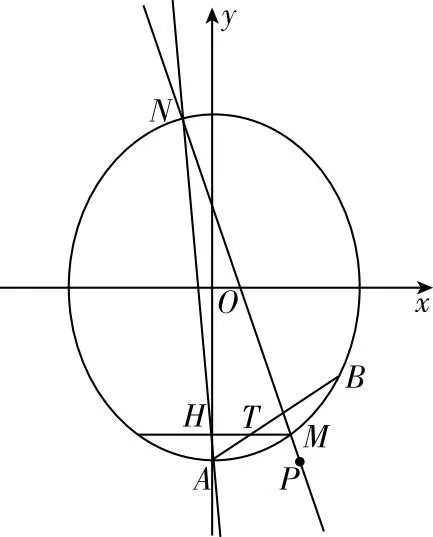
图3 2022新课标乙卷理20文21题配图
由①②③可知,y1=-λy2-2λ-2,
【题4】(2022新课标甲卷理20文21)设抛物线C:y2=2px(p>0)的焦点为F,点D(p,0),过F的直线交C于M,N两点.当直线MD垂直于x轴时,|MF|=3.
(1)求C的方程;(答案:y2=4x)
(2)设直线MD,ND与C的另一个交点分别为A,B,记直线MN,AB的倾斜角分别为α,β.当α-β取得最大值时,求直线AB的方程.
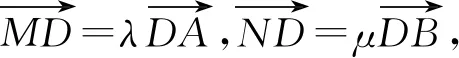
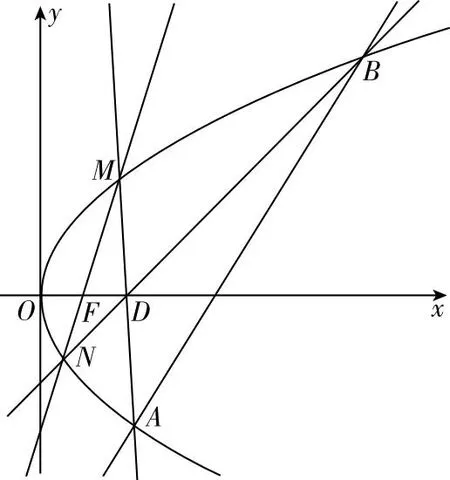
图4 2022新课标甲卷理20文21题配图
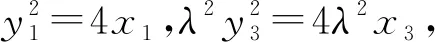
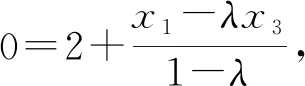


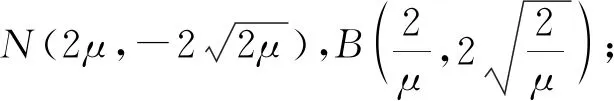
而MN为焦点弦,故x1x2=1,
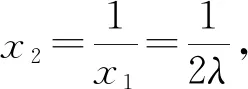
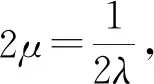
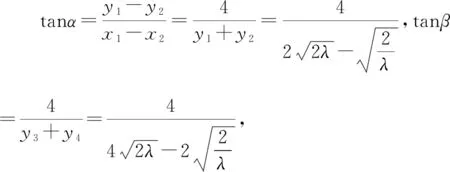
即tanα=2tanβ,要使α-β最大,显然tanβ>0,

3.四定问题展示——百花齐放,精彩纷呈
通过上述高考试题可以看出,“定比点差法”的应用极为广泛,涉及三类圆锥曲线,事实上,我们主要利用该方法来处理“四定”问题,下面结合几个模拟题进行展示.
3.1 定点问题

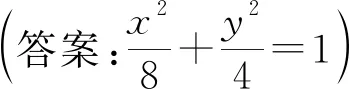
(2)记点A关于x轴的对称点为M(异于B点),试问直线BM是否过定点?若是,请求出定点坐标;若不是,请说明理由.
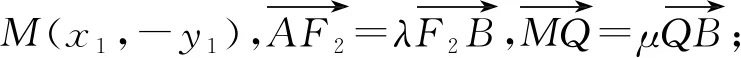
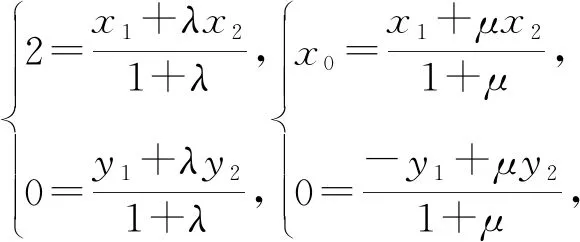
则y1+λy2=y1-μy2=0,故λ=-μ.
而M(x1,-y1),B(x2,y2)在椭圆C上,

两式相减整理得,x0(x1-μx2)=8-8μ,
即x0(x1+λx2)=2x0(1+λ)=8+8λ,
解得x0=4,故直线BM过定点(4,0).
3.2 定值问题
【题6】(2023岳阳一模)已知直线l1:y=2x和直线l2:y=-2x,过动点E作平行l2的直线交l1于点A,过动点E作平行l1的直线交l2于点B,且四边形OAEB(O为原点)的面积为4.
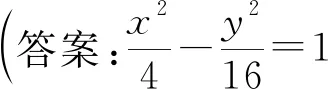
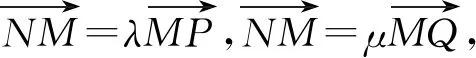
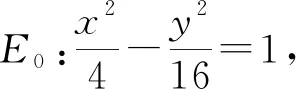
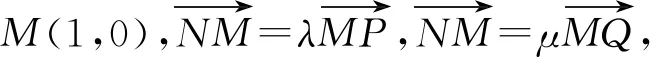

则λx1=1+λ,μx2=1+μ,
两式相加得,λx1+μx2=2+λ+μ,
相减可得,λx1-μx2=λ-μ;
同理可得,λy1-μy2=0.
因为点P,Q在曲线E0上,
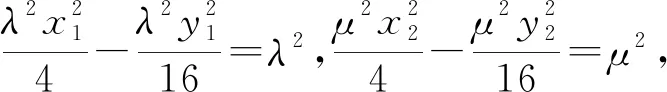

3.3 定线问题
【题7】(2023淄博一模)已知抛物线C:y2=2px(p>0)上一点P(2,t)到焦点F的距离为3,A,B为抛物线C上异于原点的两点.延长AF,BF分别交抛物线C于点M,N,直线AN,BM相交于点Q.
(1)若AF⊥BF,求四边形ABMN面积的最小值(答案:32);
(2)证明:点Q在定直线上.
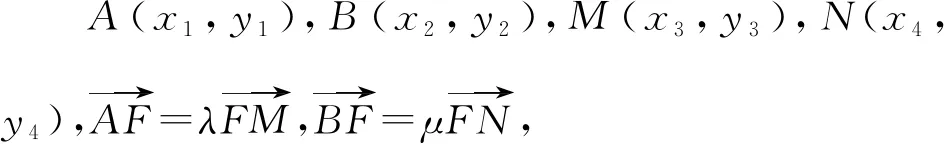
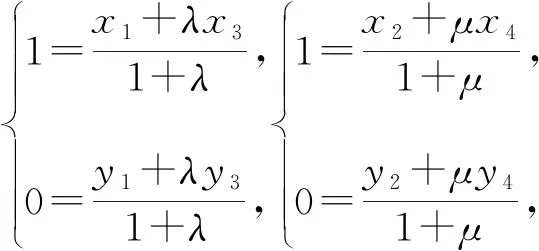


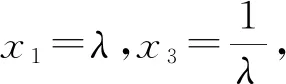

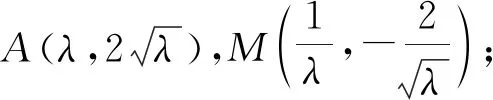
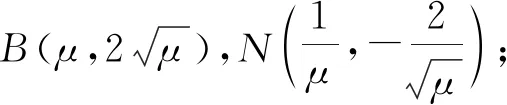
由两点弦方程可知,
直线AN:4x=(y1+y4)y-y1y4,
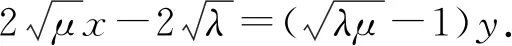
同理可得,
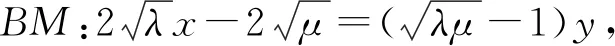
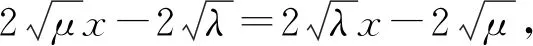
3.4 定比问题
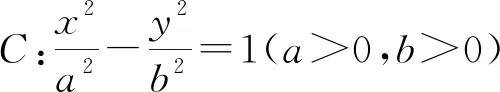
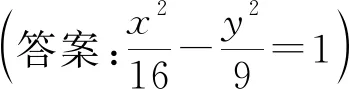


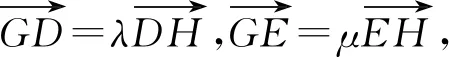
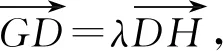
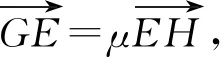
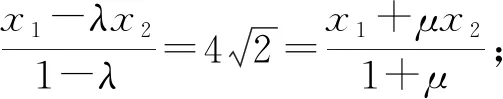
由于x1,x2是变量,故-λ=μ,即λ+μ=0,
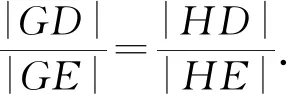
4.题后反思小结——锦上添花,画龙点睛
问题1:当题目给出哪些信息时,可以使用“定比点差法”?
答:若能从题设条件中挖掘出A,B,P三点共线,其中A,B为圆锥曲线上的动点,P为已知定点时,可以考虑使用“定比点差法”.
问题2:在利用A,B,P三点共线构建向量关系式时,要注意什么?为什么?

问题3:你能谈谈“定比点差法”的大致步骤吗?
答:①作图觅关系:绘制相关图形,在图形中寻找出三点共线的条件,其中有两个动点在圆锥曲线上,一个点为已知定点;
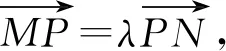
③依题乘系数:根据题设条件乘以相应的系数,若是只有一组三点共线,则一般情况下将点N满足的圆锥曲线的方程乘以λ2即可;若是有两个关系式,则一般需要将其中两个点的坐标方程分别乘以λ2,μ2;
④作差再替换:将两个方程对减,利用平方差公式分解后,再结合②中结果,根据问题的导向进行变形,此时可以使用整体替换变形,不需要求出每个点的坐标,如题5,6,8;也可以分而治之击破,即用λ,μ等未知量表示每个点的坐标,如题1,2,3,4,7.

