第三届跨区域命题征集活动成果展示(二)

本刊编辑部

【原创创新试题组】

( )

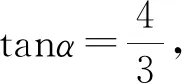
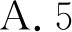
图1

【原创2】将给定的数列{an}依顺序按一定的个数用括号将其分组,可以得到以组为单位的序列(a1,a2,…,ak,…,ap),(ap+1,ap+2,…,ap+k,…ar),(ar+1,ar+2,…,ar+k,…as),…称为数列{an}的一个分群数列(其中k,p,r,s∈N+),称ak为第1群的第k个数,ap+k为第2群的第k个数,ar+k为第3群的第k个数,以此类推.已知数列{an}的通项公式为an=2n-1(n∈N+),将数列{an}按照2,3,2,3,…的个数分组得到分群数列,则此分群数列第409群的第2个数是________,若此分群数列第n群的所有的数之和为2 324,则n=________.

【原创3】“东南西北”是我们小时候经常玩的一种简单游戏,从开始玩起我们就一直称呼它为“东南西北”,取一张两面全白的正方形纸,左右对折然后展开,再上下对折然后展开,这样形成一个“田”字型,中间有两条折痕,将正方形的四个角对折进去,在中心点汇拢,形成一个新的正方形,然后整个儿翻过来,再将四个角对折进去,在中心点汇拢,这时候应该有八个小三角形两两拼成一个大三角形.如图3构建数学模型,则二面角E-AB-F的大小为

图2

图3

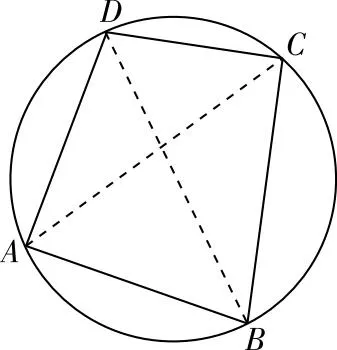
图4

图5

( )

【原创5】试题:已知函数f(x)=(x-2)ex+ax+2(其中e为自然对数的底数).

(1)当x∈[0,+∞),f(x)≥0恒成立,求实数a的取值范围;

【答案详解及创新点分析】

【原创1】

【命题意图】本题考查三角函数、解三角形、基本不等式知识点

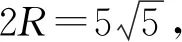
设四边形周长为l=AB+AD+BC+CD,

BD2=AB2+AD2-2AB·AD·cosα,

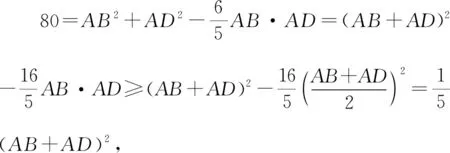
∴(AB+AD)2≤400,即AB+AD≤20,当且仅当AB=AD=10时取到最大值.

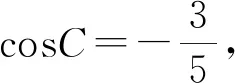
设∠ADC=β,

在三角形ACD中,AC2=CD2+AD2-2CD·AD·cosβ=125-100cosβ①,

在三角形ABC中,AC2=AB2+BC2-2AB·BC·(-cosβ)=125+100cosβ②.

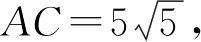
【创新点分析】该题将数学文化和三角函数、解三角形及基本不等式有机结合在一起,本题利用三角函数和解三角形列出式子,利用基本不等式求解.难度适中,有一定的综合性.

(原创命题人:高洪波 新疆哈密市第十五中学)

【试题评语】本题将生活实际和三角函数、解三角形及基本不等式有机结合在一起,难度中等,通过三角函数和解三角形列出式子,观察等式结构形式,利用基本不等式求解.

(评语老师姓名、单位:魏清泉 青岛市教育科学研究院)

【原创2】

【命题意图】本题以新定义题型考查数列的知识,考查数学阅读理解能力与逻辑推理、数学运算的核心素养.

【解题思路】(1)按照分群数列的定义,数列{an}为1,3,5,7,9,… (1),数列{an}的2,3分群数列为(1,3),(5,7,9),(11,13),(15,17,19)… (2),将数列(1)重新分群,按每个群含5个元素的方式得到分群数列:(1,3,5,7,9),(11,13,15,17,19)… (3),对照分群数列(2)与(3),容易知道分群数列(3)中的每个群是分群数列(2)中的2个群组成,由409=2×204+1,可知分群数列(2)的第409群的第2个数是分群数列(3)的第205群的第2个数,由5×204+2=1 022,可知分群数列(3)的第205群的第2个数是数列(1)的第1 022个数,由于等差数列:1,3,5,7,9,…的通项公式an=2n-1,由2×1 022-1=2 043,所以分群数列(2)的第409群的第2个数是2 043.

(2)对n分偶数和奇数两种情况进行讨论.

若n为偶数,则n=2k,则数列(2)的第n群的数是数列(3)的第k群的第3,4,5个数,由于数列(3)的第k群的第5个数是10k-1,所以数列(2)中的第n群的元素之和为(10k-5)+(10k-3)+(10k-1)=30k-9=15n-9,令15n-9=2 324,无整数解,不符合题意;

若n为奇数,设n=2k+1,则数列(2)的第n群的数是数列(3)的第k+1群的第1,2个元素,由于数列(3)的第k+1群第1个元素是10k+1,所以数列(2)中的第n群的元素之和为(10k+1)+(10k+3)=20k+4=10n-6,令10n-6=2 324,得n=233,符合题意.综上,n=233.

【创新点分析】本题通过“分群数列”的新定义问题,旨在回归数列问题的本质:即对一组按一定顺序排列的数的规律性的认识,通过观察、联想、归纳、分析、论证,反映了人们对周围世界的认识过程,展示了知识发生发展的思维过程.在考查角度和维度上,一方面考查了学生的数学阅读理解能力,另一方面拓展了学生对数列的进一步认识.在题型选择上,以双空题的形式,便于学生的发挥数学直觉,灵活应用本题隐藏的数字排列规律.在设问上,遵循递进原则,第一问是考查数感,通过5个数的重新组合,发现规律,实现思维的跃迁;第二问分为n是奇数和偶数两种情况,考查了学生思维的严谨性和全面深刻性,对思维提出了更高的要求.

(原创命题人:师斌 新疆哈密市第十五中学)

【试题评语】对数列进行新定义,是数列题目创新的一种重要方法.双空题遵循从特殊到一般的出题思想,层层递进,符合知识发生发展的思维过程.

(评语老师姓名、单位:魏清泉 青岛市教育科学研究院)

【原创3】

【考查维度】考查了数学建模、直观想象、数学运算等核心素养.

学生面对实际问题不会分析,缺少数学建模能力,平时课堂落实数学建模核心素养有所欠缺,实际问题缺乏合适的素材,课堂时间紧,不能抽出足够多的时间让学生参与到对实际问题进行建模,从而使得学生在分析问题和解决问题的能力方面不足,知识综合运用能力较差,通过这道题,以试题的考查为导向,引导课堂教学回归到新课标要求引导学生多动手动脑,增强学生的分析问题和解决问题的能力.

(原创命题人:徐敏 江西省莲花中学)

【试题评语】本题以“折纸”为载体,角度新颖,来源生活,主要考察了直观想象能力与数学建模能力.考察了二面角的求解,构思较为巧妙.

(评语老师姓名、单位:魏清泉 青岛市教育科学研究院)

【原创4】

【命题意图】本题以分段函数为背景,考查函数与方程,考查学生逻辑推理核心素养,考查转化与化归思想和数形结合思想.

【创新点分析】函数较多考查的是单调性,本题题干简洁精练,同样考查了函数的单调性和多变量转换成单变量及数形结合思想.但本题还涉及函数与方程之间的关系,法一直线与曲线相切,法二多变量的处理,让人不易想到,怎么联系所求与题干便能充分调动学生的思考,考查学生的转化与化归思想,|x1-x2|≤2转化成|x1-x2|max≤2.本题是一道难得的好题,对学生的思维能力有要求.

(原创命题人:朱冰 江西省瑞金第一中学)

【试题评语】本题以分段函数为背景,考查函数与方程、转化与化归、数形结合思想,突出考查函数的单调性、逻辑推理能力,试题难度中等.

(评语老师姓名、单位:魏清泉 青岛市教育科学研究院)

【原创5】

【命题意图】本题考查了已知不等式恒成立求参数的取值范围、导数在证明数列不等式的应用、数列的项和关系及不等式的同向可加性,突出考查了导数在研究函数单调性的应用.考查了抽象概括能力、推理论证能力和运算求解能力,考查了函数与方程思想和转化与化归思想,体现了数学抽象、数学运算和逻辑推理等数学核心素养.

【解题思路】(1)由f(x)=(x-2)ex+ax+2知f(0)=0,f′(x)=(x-1)ex+a,

要使f(x)≥0在[0,+∞)上恒成立,至少满足f′(0)=-1+a≥0,即a≥1.

另一方面,当a≥1时,f′(x)=(x-1)ex+a≥(x-1)ex+1.

记g(x)=(x-1)ex+1,则g′(x)=xex,

显然g′(x)≥0在[0,+∞)上恒成立,故g(x)在[0,+∞)上单调递增,

故g(x)≥g(0)=0,故f′(x)≥0在[0,+∞)上恒成立,从而f(x)在[0,+∞)上单调递增,

故f(x)≥f(0)=0.

故实数a的取值范围为[1,+∞).

(2)由(1)知(x-2)ex+x+2>0对一切的x∈(0,+∞)恒成立,

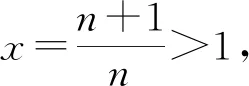
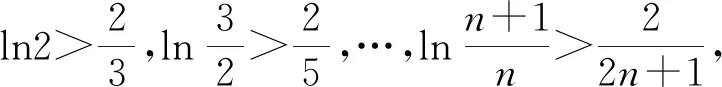
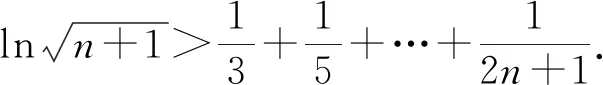
证毕.

【方法技巧】对于已知不等式恒成立求参数范围的题型,常见的方法有两种:一是最值法,即直接构造函数,再研究它的相应最值来解决;二是分离参数法,即把参数分离到不等式的一边,再研究分离后函数的最值,实现求解.小技巧是可以用点效应对参数范围进行限制,但要注意逻辑的完备性.对于数列不等式的证明问题,一般思路是将不等式的两边理解为两个数列的前n项和(分别记数列{an},{bn}的前n项和为Sn,Tn),要证明Sn

【高考风向】本题与2022年全国新高考Ⅱ卷第22题的设计思想类似,这类题能很好地考查学生分析问题与解决问题的能力.

(原创命题人:谢小平 江西省瑞金第一中学)

【试题评语】本题以数列和导数为载体,考查导数研究函数单调性的应用、不等式恒成立、导数证明不等式等,考查了抽象概括、推理论证和运算求解能力,考查数学抽象、数学运算和逻辑推理等素养,难度较大.

(评语老师姓名、单位:魏清泉 青岛市教育科学研究院)