立足核心素养 培养关键能力
——2023年全国乙卷解几大题的多解、推广及变式探究
王东海
(安徽省合肥市肥东县城关中学)
直线与圆锥曲线的位置关系问题一直是高考的热点和难点,在这类考题的命题中往往都是探求一些特殊结论,这些结论看似特殊,实则往往都具有普遍性.我们在解答考题后要深入拓展到一般情况,还要注意探寻其他圆锥曲线的对偶性质.下面以2023年高考全国乙卷(理科)第20题的圆锥曲线试题的变式探究为例进行说明.
1 真题呈现
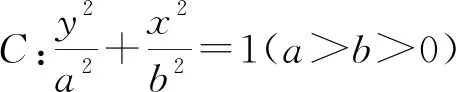
(Ⅰ)求C的方程;
(Ⅱ)过点(-2,3)的直线交C于P,Q两点,直线AP,AQ与y轴的交点分别为M,N,证明:线段MN的中点为定点.
【分析】该题考查了学生的逻辑推理、数学运算、直观想象等数学素养,具有很好的选拔功能.第(Ⅰ)问求椭圆方程,难度较低.
第(Ⅱ)问证明定点既可用常规的直曲联立处理,又可采取齐次化加以解决,还能使用定比插参的技巧求解.考题简洁但具有较大探究空间.
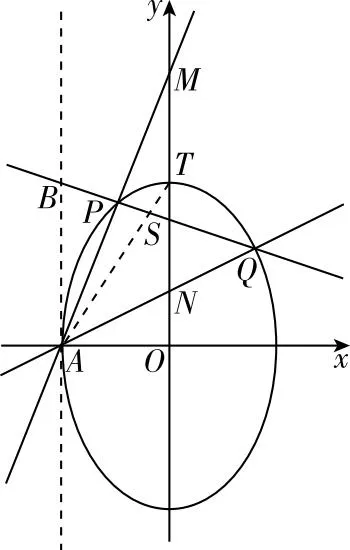
图1 考题曲线图
2 解法探究
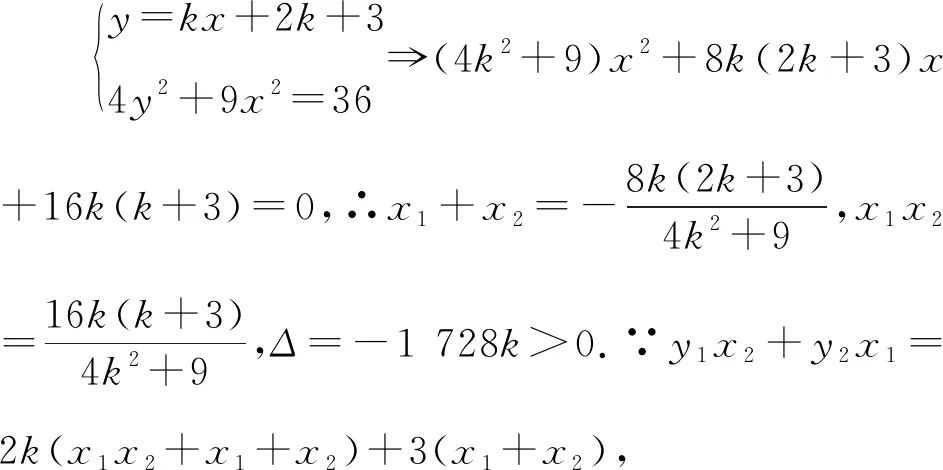
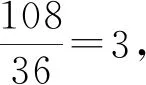
【评注】先设出直线并与椭圆联立,再设而不求结合韦达定理表示出M,N中点的纵坐标,最后消去参变量可得中点为定点,这是处理此类问题的通解通法.但对学生计算能力要求较高.
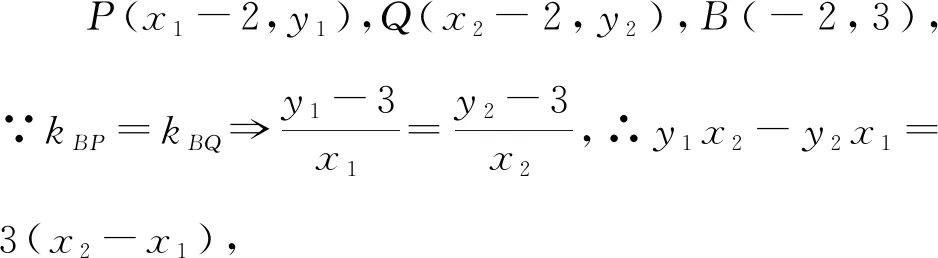
【评注】此解法直曲不联立,而是通过巧妙设点,利用点在椭圆上等坐标间的运算处理此题.此解法在设出P,Q两点的坐标时采取向左平移2个单位的设法,是解题的关键.

【评注】考虑到点P,Q在椭圆上,从而设点时采取半角换元的设点方法,可使计算量变少.
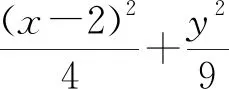
【评注】本解法先将整个图形向右平移,使得两直线AP,AQ的斜率之和易求,再用齐次化技巧表示出斜率之和,从而与之关联的中点坐标可以求出.

【评注】利用过两条直线的曲线系恰为考题所给椭圆,对比两者之间系数,从而得中点为定点.
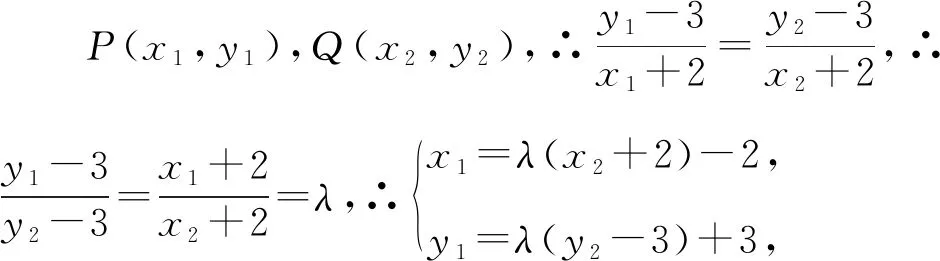
【评注】本解法先将三点共线所得比例设为定比λ,再用λ表示出所求中点纵坐标,后消去λ即可得中点为定点.
3 背景探究
近年来,命题者开始挖掘高等几何中一些素材来命制高考中的圆锥曲线试题,而这其中被关注的较多的是具有极线背景的圆锥曲线试题.本题有着丰富的射影几何背景,克莱因曾说:基础数学的教师应该站在更高的视角来审视、理解初等数学问题,只有观点高了,事物才能显得简单明了.为了将原理阐述清楚,下面先共同来探讨一下本题涉及的概念和性质:
3.1 调和点列和调和线束
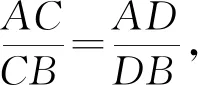
【调和线束定义】如果直线上点列A,B,C,D为调和点列,则此直线外一点M分别与这四点相连接形成的四条直线称为调和线束.
【定理1】任意一条不经过点M的直线与调和线束中的每一条直线都相交,那么四个交点依然成调和点列.
3.2 极点、极线
【代数定义】设两点C,D的连线与圆锥曲线Γ相交于A,B,若线段AB被C,D调和分割,则称C,D是关于圆锥曲线Γ的一对调和共轭点.而一点P关于圆锥曲线Γ的所有调和共轭点的轨迹为一条直线p,此时称直线p为点P(关于Γ)的极线,点P称为直线p(关于Γ)的极点.简称极.
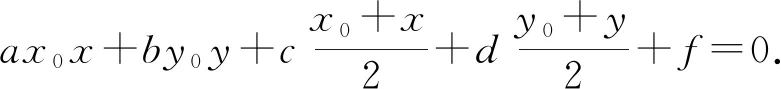
【性质2】点P是圆锥曲线G的一个极点,它对应的极线为l,过点P任意引一条直线交l于点Q,交G于点A,B,若点A是位于P,Q间的点,则P,Q必调和分割线段AB.
运用上述背景知识,此题可以高观点低运算进行处理:
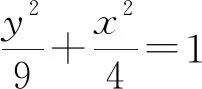
这道高考题是利用直线截调和线束所得交点仍成调和点列这一极点极线的性质,并考虑高中生能力可做来进行命题的.掌握了这一命题背景,还可利用y轴以外的其他直线去截调和线束,从而命制多个考题.比如用x轴、其他直线去截调和线束等.
4 变式探讨
4.1 条件变式

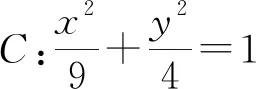
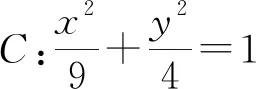
简证:采用下面拓展推广的结论3证法,得变式1,2,3的线段MN的中点分别为定点A,T,T.
4.2 类比变式

【变式5】过抛物线C:y2=4x外一点B(-2,1)的直线与C交于P,Q两点,过B点作椭圆C的两条切线,切点分别为A,T两点,过T点作平行于AB的直线l,直线AP,AQ与l的交点分别为M,N,证明:线段MN的中点为定点.
【变式6】过点B(-4,3)的直线交圆C:(x-2)2+(y-1)2=1于P,Q两点,过B点作圆C的两条切线,切点分别为A,T两点,过T点作平行于AB的直线l,直线AP,AQ与l的交点分别为M,N,证明:线段MN的中点为定点.
简证:也采用下面拓展推广的结论3证法,得变式4,5,6的线段MN的中点分别为定点T.
5 拓展推广
由上面的分析,可得线段MN的中点为定点T.那么此结果是偶然还是必然呢?考虑将考题第(Ⅱ)问推广至一般情形,可得下面结论:
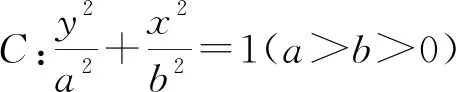
若将上面的椭圆变为焦点在x轴上的椭圆,则可得:

若再将截调和线束的直线x,y轴推广至一般的平行线时,则可得:

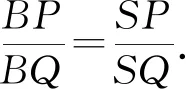

图2 结论3曲线图
6 逆向探究
若将结论3的条件与结论反过来,考虑其逆命题是否成立?

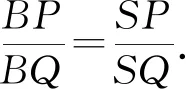

图3 结论4曲线图

图4 例题1曲线图
7 类比探究
将椭圆的结论3,4类比到双曲线及抛物线,可得以下几个结论:
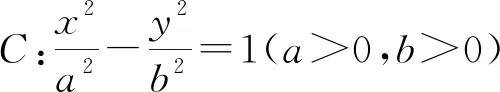
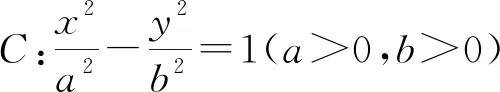
【结论7】过抛物线C:y2=2px(p>0)外一点B(m,n)的直线与C交于P,Q两点,B点关于C的极线交C于A,T两点,过T点作平行于AB的直线l,直线AP,AQ与l的交点分别为M,N,则线段MN的中点为定点T.
【结论8】过抛物线C:y2=2px(p>0)外一点B(m,n)的直线与C交于P,Q两点,过B点作抛物线的两条切线,切点分别为A,C,过P点作平行于AB(AC)的直线l,直线AC与l的交点为T,且P关于T的对称点为N,则直线QN必经过定点A或C.
8 高考溯源
在圆锥曲线的考查中,此类定点问题近几年经常出现,时常会成为学生心中的“痛点”,但如果掌握了极点极线的相关理论,则能够比较轻松地啃下这个“痛点”.

(Ⅰ)求椭圆C的方程;
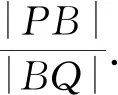
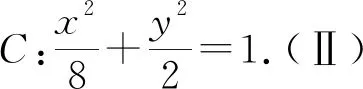
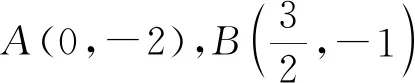
(Ⅰ)求E的方程;
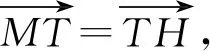
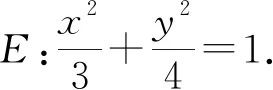
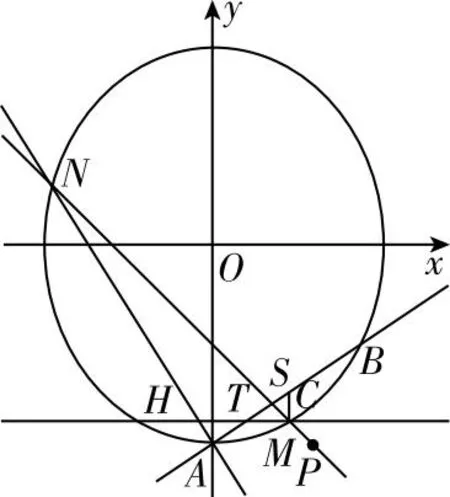
图5 例题2曲线图
9 结语
在数学学习中,时常会遇到各种各样的问题,这时我们不能满足于将问题解决了就万事大吉,而是要进一步进行探究.我们可以将问题一般化,进行拓展研究,还可以进行变式研究,怎么样能让学生深刻掌握.总之,探究必须植根于具体问题之中,探究是一个计划、行动、反思,再计划、再行动、再反思的过程.探究是一把金钥匙,能够帮助我们打开智慧殿堂的大门,教学中要为学生提供探究的机会,让学生在探究中体会到学习的快乐,让探究成为一种习惯.

