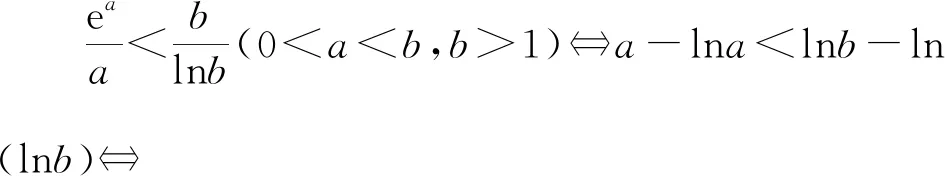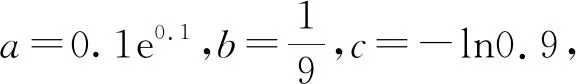指向“通性通法”的一类数式大小比较问题
张隆亿
(福建省永春第一中学)
章建跃博士指出,解题教学中注重“通性通法”是一种追求长期利益的有效途径.其中,“通性”指的是数学概念所蕴含的基本性质,它们是解决问题的关键特征.而“通法”则强调利用这些基本性质所提供的思想方法来解决各类问题.在解题教学中,深入理解数学概念的本质和背后的通性,学生不仅能够解决当前问题,还能够应用这些通性通法解决更广泛和复杂的问题,也使他们在数学学习和实际生活中受益终身.

命题手法1 已知方程f(a,b)=0,比较a,b的大小
这类试题以方程f(a,b)=0为条件,比较a,b的大小.一般以选择题形式进行考查,往往以指数、对数函数和不等式为载体,考查数学抽象、逻辑推理、数学运算等核心数学素养,注重考查思维品质和关键能力,具有良好的区分度.将方程f(a,b)=0转化为m(a)=n(b),观察方程左右两边结构,通过放缩同构为不等式g(a)≤g(b).构造函数y=g(x),结合函数y=g(x)的单调性将不等式g(a)≤g(b)转化为a,b的大小,从而达到化繁为简的目的.
【例1】(2020新课标Ⅰ理科12题)若2a+log2a=4b+2log4b,则
( )
A.a>2bB.a<2bC.a>b2D.a 【分析一】方程2a+log2a=4b+2log4b左右两边式子结构比较相近,结合选项比较a与b2,2b的大小,变形为2a+log2a=22b+log2b<22b+log22b,不等式两边的结构相同,构造函数f(x)=2x+log2x,所以不等式可化为f(a) 【评析】本解法将方程2a+log2a=4b+2log4b转化为2a+log2a=22b+log2b,观察方程左右两边结构,通过放缩同构为不等式2a+log2a=22b+log2b<22b+log22b.构造函数f(x)=2x+log2x,结合函数y=f(x)的单调性将不等式f(a) 【分析二】设t=2b,则方程2a+log2a=4b+2log4b可化为2a+log2a=2t+log2t-1.构造函数f(t)=2t+log2t-1-2a-log2a,则函数y=f(t)在(0,+∞)上为增函数且有零点t=2b.由f(a)=-1<0,f(2a)=2a(2a-1)>0得a<2b<2a,所以b 【评析】本解法将方程f(a,b)=0转化为含参数t的方程g(t)=0,构造函数y=g(t),则函数y=g(t)有零点t,结合函数y=g(t)的单调性及零点存在定理确定零点的范围,从而得到零点t=2b与a的大小关系,从而达到化繁为简的目的. 命题手法2 已知不等式f(a,b)<0,比较a,b的大小 这类试题以方程f(a,b)<0条件,常将变量a,b分离,同构为g(a) ( ) (1)积型aea (3)和差型ea+a 命题手法3 已知不能直接比较大小的确定常数a,b,c,比较a,b,c的大小 ( ) A.a C.c 【评析】本题是三个不能直接比较大小的含指数、对数的确定常数比较大小的选择题.解法中挖掘出了公共的常量0.1,将三个数转化为三个函数值,再通过两边取对数得到lna-lnb=0.1+ln(1-0.1),构造函数f(x)=x+ln(1-x),x∈(0,0.1],结合函数f(x)=x+ln(1-x),x∈(0,0.1]的单调性,得到f(0.1) 在教学中,我们经常发现,学过和练过的知识在考试中却无法取得高分.究其原因:我们在讲练习时注重具体题型和技巧,却忽视了培养学生的“通性通法”,导致学生的学科素养没有得到有效提升,造成教与学脱钩,教学效率低下.因此,我们应该遵循“课程标准”,重视基础知识、基本技能的掌握途径,提升数学核心素养.这样的改进不仅能够带来眼前的利益,也能为学生的长远发展打下坚实的基础.数学竞赛亦如此,2022年全国高中数学联合竞赛加试试题(A卷)第一题:如图,在凸四边形ABCD中,∠ABC=∠ADC=90°,对角线BD上一点P满足∠APB=2∠CPD,线段AP上两点X,Y满足∠AXB=2∠ADB,∠AYD=2∠ABD.证明:BD=2XY. 这道平面几何题对学生的要求体现了近年来数学竞赛对平面几何能力的要求,强调了基本知识、定理和方法的应用.然而,赛后反馈显示,许多学生在面对条件“∠AXB=2∠ADB,∠AYD=2∠ABD”以及“∠APB=2∠CPD”时感到束手无策,不知所措.这提醒我们在平时训练学生时要更加积极地探索解题思路的合理性,尽管存在多种思路与方法,但通性通法应成为首选. 通过对近年来高考和高考模拟中数式比较题的分析,我们可以发现这样的规律:对数函数模型、三角函数模型等典型函数模型的数式大小比较问题,频繁出现在各类考试的选择题中,难度有大有小.虽然形式看起来可能有很多变化,但万变不离其宗.如果我们能从数式大小比较问题的通性通法入手,深入了解构造函数法适用条件及解题步骤,然后运用函数的单调性,突破数式大小比较解题障碍点.学生通过运用“通性通法”,能够灵活应用已学知识解决问题,不仅在短期内取得好成绩,还能培养数学素养和解题能力,为长期发展打下基础.此外,我们在教学中不仅要关注一题多解,更需要关注多题一解,注重通性通法,淡化技巧,回归数学本质,鼓励学生勤动手、勤反思,多操作、多思考,提升了数学核心素养,感受了“用数学的眼光观察世界,用数学的思维思考世界,用数学的语言表达世界”的精神内涵.


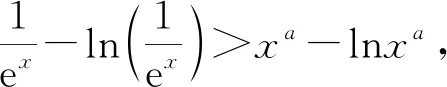
1.利用x=lnex,x=elnx(x>0)进行幂指、幂对转换同构
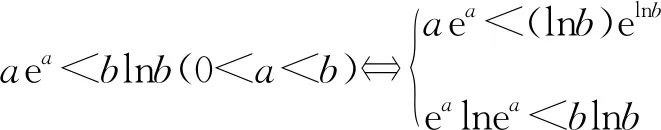
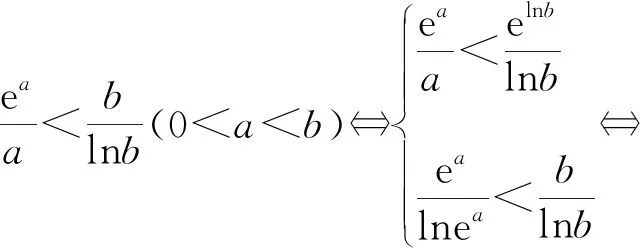
2.对等式、不等式两边取指数、对数进行同构