自主探索 引导发现

陈方

摘 要：本文以“自主探索”为主线，引导学生通过观察、操作、交流、探索等活动发现数学规律，建构“三角形边的关系”模型，让学生在亲身经历中体验了数学发现之美、抽象之美，充分发挥了学生的主体作用，培养了学生数学素养，提升了教学有效性.

关键词：自主探索；数学发现；数学素养

在小学数学课堂，虽然师生互动频繁，但是师生互动大多以“师问生答”为主.“师问生答”看似“以生为主”，体现了学生的主体价值，然实际上却依然延续着“以师为中心”的教学模式，学生的思路被教师牵着走，学生的学习形式依然为被动接受，学生探索数学和发现数学的能力也没有得到实质性的提升［1］.基于此，教师在教学中应设计一些自主探索活动，以此激发学生深度思维，提升学习品质.

在探索“三角形边的关系”时，笔者以实践活动为主线，通过实验、观察、分析、抽象等教学活动，引导学生通过自主探索建构数学模型，以此激发学生数学意识，培养学生数学能力.

1 教学分析

在探索该内容前，学生已经知晓三角形有3条边、3个顶点、3个角，知晓什么是“首尾相连”，这些内容为本节教学的顺利开展做好了知识上的准备.探索“三角形三边关系”的实验易于操作和理解，符合学生的认识水平，这也为开展自主探索活动，培养学生独立思考能力提供了良好的契机.加之小学生动手能力强，想象力丰富，敢于探索和交流，这些优秀的品质和能力都为建构高效课堂提供了重要保障.

2 课前互动

师：现在我们一起玩个游戏好不好.（听说玩游戏，个个兴奋不已）

师：现在跟着老师一起做，双手张开，十指相对，然后从拇指依次打开，是否能够打开呢？（学生与教师一起动手游戏）

生齐声答：可以.

师：很好，如果像这样，中指弯曲，其他手指两两相对，这时有两个手指打不开了，猜一猜会是哪两个呢？

生2：食指.

生3：无名指.

生4：小拇指.

师：现在我们该怎么办呢？

生5：我们可以动手做啊，试试不就知道了吗？

师：很好！其实学数学有时和玩游戏一样，当难以得到结论时，不妨动手试一试，可能会收获意外的惊喜哦！

【设计意图】教师在课前设计游戏环节，其目的主要有两个：一是为学生建构一个平等的、自由的、和谐的学习氛围，活跃了课堂氛围，拉近了师生距离；二是引导学生在遇到问题时可尝试通过“动手做”来解决问题，培养学生“实践出真知”的探索精神.

3 教学过程

片断1 提出问题，初步探索

3.1 回顾旧知，提出问题

师：大家看一下，这些是什么图形？（教师PPT展示三角形图形）

生齐声答：三角形.

师：根据已有经验说一说，三角形中都有什么呢？

生1：三角形有3条边、3个顶点、3个角.

师：很好，今天我们就先来研究3条边.

师：3条边相当于什么呢？直线？线段？

生齐声答：线段.

师：这样问题就转化为研究3条线段，那么是不是任意3条线段都可以呢？（有的学生回复“是”，有的学生回复“不是”）

师：看来这个问题大家存在不同的看法，那么接下来我们要怎么办呢？刚刚游戏环节我们是如何处理的呢？

生齐声大：动手试.

3.2 动手实验，初步探索

师：老師为大家准备了5根长度和颜色均不同的小棒，现在将小棒看成线段，开启探究之旅.该实验以小组合作的方式进行，请各组组长安排好实验员和记录员.实验步骤：① 分别测量5根长度并记录（按照颜色做好登记）；② 任意选3根“拼一拼”，记录实验结果及实验数据.实验过程大家都清晰了吗？

生齐声答：清楚了.

接下来教师预留时间让学生实验、记录、发现.

【设计意图】在教学中，教师从学生已有认知出发，带领学生回顾了三角形的特征，引出本节重点研究的内容“3条边”.在教学中明确三角形都有3条边，并强调“3条边”也就是“3条线段”，为后面探究长度扫清了障碍.另外教师伺机设问，诱发学生对“任意长度的线段”进行猜想，引出本节课研究的主题.在猜想中学生产生了分歧，继而激发学生“动手试”的热情，为接下来的动手实验做好了知识准备和情感基础，有助于提升实验效果.在初步探索阶段，教师将主动权交由学生，为学生营造了自主探索和合作交流的教学环境，鼓励学生通过“动手试”去感知三角形三边的关系，同时要求学生记录实验结果，继而为后面探索三角形边的关系提供了数学依据.

片断2 展示交流，深入探索

师：各组基本已经实验完毕了，你们的实验结果是什么？

生2：有些可以拼，有些不可以拼.

师：是吗？（生点头表示赞同）

师：好的.现在我们一起来分析实验结果.

师：现在我们分别拿出1cm、2cm和4cm的小棒，结合你们的实验结果说一说，你们有没有围成三角形呢？

生3：实验结果是“不能”.

师：大家现在重新动手做一做，真的不能围成吗？（生继续实验）

生3：还是不能.

师：是吗？为什么我拼成了呢？（教师投影展示自己的拼图结果，图1）

师：我这个不是三角形吗？

生4：不是，三角形的三边是首尾相连的.

师：哦！我竟然把“首尾相连”忘记了.如何将两根短的小棒继续往下压是不是就可以了呢？（教师动手操作，并投影展示实验过程）

师：已经压到了极限，还是不行，看来1cm、2cm、4cm这三根小棒确实围不成.

师：如果用1cm、2cm、3cm这三根小棒拼呢？

生5：这个也拼不成.

师：具体说一说，为什么不能拼呢？你有什么发现？

生5：因为两根短的小棒拼在一起刚好和长的小棒一样长，我们也尝试让两个短的拱起来一点，但是一动两个小棒就分开了，所以不能围成三角形.

师：说得很好，我们一起动手做一做，验证一下，是不是这样呢？（教师让学生动手拼，为后期揭示三角形边的关系打下坚持的基础）

师：刚刚我们分别用1cm、2cm、4cm和1cm、2cm、3cm拼都失败了，谁来提供一组能够围成三角形的数据呢？（教师让学生从自己的汇总表里查询）

生6：用2cm、3cm、4cm能够围成.

师：很好，我们一起“拼一拼”.（教师继续投影展示实验过程）

师：我们成功了吗？

生7：成功了.这个图形有3条边、3个顶点、3个角，3个小棒首尾相连，符合三角形的特征.

【设计意图】通过刚刚的实验，学生得到不同的实验数据.为了便于学生发现规律，教师将实验结果分为“不能围成”和“围成”两种情况进行讨论.对于不能围成的情况，教师又将其分为了两种情况，分别为两边之和小于第三边和两边之和等于第三边.对于两边之和小于第三边的情况，是明显围不成的，在此环节重点强调“首位相连”的问题.对于两边之和等于第三边，教师引导学生在操作、观察、实验的基础上，用自己的语言进行表达，其目的引导学生关注三边间的长度关系，为后面建构三边关系模型架桥铺路.有了前面两种不能围成的经验，学生在理解围成的情况自然也就水到渠成了.相信，通过以上探究，不仅深化了学生对三角形定义及特征理解，而且也让学生对三根小棒的长度关系有了一定的感知，有利于后期的探索发现.

片断3 探索发现，建构模型

3.3 引导思考，揭示主题

师：看来现在有3条线段还不够，还需要满足一定的条件，那么这个条件会和什么有关呢？

生8：与线段的长度有关.

师：很好，现在我们再重新回顾一下刚刚共同实验的过程：第一次我们拿出了3根长度分别为1cm、2cm和4cm的小棒，结果不能围成；第二次又用1cm、2cm、3cm三根小棒拼，结果又失败了；第三次用长度分别为2cm、3cm、4cm的拼，终于围成的三角形.（教师板书实验数据及结果，便于学生对比）

师：这些小棒代表三条边，研究小棒的长度关系其实就是研究三角形三边的关系，这也就是我们今天要研究的重点.

师：观察图形并结合以上数据，思考一下：若想围成三角形，3条线段的长度到底有什么样的关系呢？（学生独立思考后，进行小组交流）

3.4 互动交流，建构模型

师：谁来分享一下你们的交流结果？

生9：我发现两条短的线段的长度之和要大于那条长的线段.

师：能够具体说一说吗？

生9：在第一种情况中，三条线段的长度分别为1cm、2cm、4cm，两条较短的线段之和为3cm，小于4cm，没有围成三角形.利用这种方法我又验证了其他两种情况，发现第二种情况是两个较短的线段之和等于第三条线段，没有围成三角形，而第三种情况，两条较短的线段的长度之和为5cm，大于4cm，围成了三角形.

师：很好.思考一下：是否可以将“两条短的线段之和”改成“任意两条线段之和”呢？

生10：可以，任意中就包含两条短的，而若两条短的相加都比长的长，那么一长一短相加肯定比短的长.

师：很好！请大家思考一下，对于第三种情况，如何用数学式子来表示这样的关系呢？

生11：2+3＞5，2+4＞3，3+4＞2.

师：你们同意他的想法吗？

生齐声答：同意.

师：现在请大家从实验结果中任选两组能够围成三角形的数据，看看是否也满足以上的条件呢？（生积极验证）

师：是否满足呢？

生齐声答：满足.

师：现在请大家再根据自己的结果分析一下，有没有不能围成的三角形也满足以上条件呢？（生又继续验证）

这样通过观察、实验、对比，最终总结归纳出了三角形边的关系，即任意两边的和大于第三边.

3.5 结合教材，巩固强化

接下来，教师让学生完成相应的教材练习，教师巡视学生练习情况，从练习反馈来看，大多学生可以熟练应用三角形三边的关系解决问题了.

师：今天所学内容大家还有什么疑问吗？（生表示没有疑问，已经理解和掌握了今天所学内容）

师：现在我就来考考大家，看看大家是不是真的没有问题了呢？

师：现在任意画一个三角形，已知三角形的三边长分别为a，b，c，你能用数学式子来表示它们的关系吗？

生12：这个简单，把刚刚具体数换成字母就可以了，也就是a+b＞c；a+c＞b；b+c＞a.

师：太棒了，看来大家个个都是学数学的小能手.

【设计意图】数学概念、公式、定理等内容的形成往往需要一个逐步抽象的过程.为了提升学生的数学抽象能力，教师有必要在教学中安排一些自主探究活动，引导学生通过观察、实验、对比等数学活动，将感性认知升华至理性结论，以此提升学生发现数学的能力［2］.在以上建构数学模型的过程中，教师分三步展开，先是提出问题，明晰并不是任意三条线段都能围成三角形，由此引发对线段长度的思考；接下来通过数据分析，建构数学模型；最后借助具体应用，引导学生化特殊为一般，以此深化学生对数学模型的理解.

片断4 应用模型，体验价值

师：既然大家已经熟练地掌握了本节所学的内容，接下来我们体验一下，在生活中有哪些重要的应用吧.（教师PPT给出题目）

问题1：小明爸爸准备钉一个三角木架，他选取了两根长度分别为50cm和35cm的木条，现在还剩下四根长度分别为85cm、15cm、100cm、50cm的木条，他一时不知道选哪个好，你能帮帮他吗？

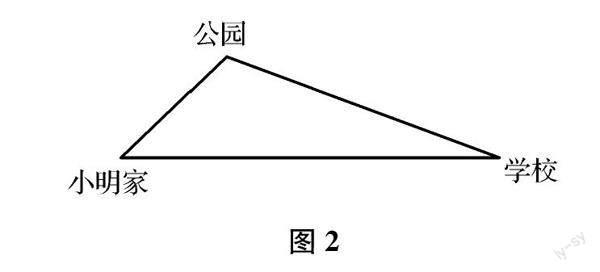
问题2：如图2，如果你是小明，你会选择哪条路回家呢？

【设计意图】引导学生利用所学知识解决现实问题，既体现了数学的应用价值，又提升了学生灵活应用数学的能力，有助于提升学生数学应用意识，激发学生数学热情.

4 教学思考

在教学三角形边的关系时，教师打破了“師讲生听”的教学模式，在教学中以自主探索为主线，引导学生发现了数学规律，建构了数学模型［3］.在教学中，教师从学生已有经验和已有认知出发，借助游戏、实验等活动环节紧紧地吸引了学生的注意力，为精彩的课堂生成奠定了坚实的基础.同时，教师在设计自主探索环节时，遵循学生的认知发展规律，设计了不同层次的探究活动，如先让学生通过“动手拼”直观感知不是任意三条线段都能围成三角形；接下来，引导学生对围成和不能围成的情况进行分析，启发学生关注三条线段的长度关系；最后，通过对比分析，逐渐建构数学模型.另外，在教学中，教师巧妙地应用设问，诱发学生进行深度思考.如在教学中两次重点强调了“任意”，一是“是否任意三条线段都能围成三角形”，以此引导认知冲突，激发学习动机；二是对“是否需要满足任意两边之和大于第三边”，这样通过设问，诱发学生进行反思、质疑，有助于知识的深化.

总之，教师要从学生出发，结合学生实际学情精心设计数学活动，引导学生在活动中学会观察、学会探索，学会抽象，以此落实学生数学核心素养.

参考文献：

［1］ 熊灿梅.探究式教学在小学数学教学中的应用［J］.中国校外教育，2014，505（35）：41.

［2］ 吴善虎.让“以学为中心”的课堂真正落到实处［J］.江苏教育研究，2017（12）：3941.

［3］ 康文平.浅谈小学数学课堂教学有效性的探究［J］.数学大世界（教师适用），2011（11）：71.

［4］ 韩方廷.新课标下初中数学课堂教学有效性策略分析［J］.中国教育学刊，2019（S1）：5456.

［5］ 梁全才.如何实现小学数学课堂的有效教学［J］.数学学习与研究，2022（26）：149151.

［6］ 夏玉钦.实现数学课堂教学有效性的五大要领［J］.课程·教材·教法，2009，29（12）：5257.