指向学习单元的高中数学可视化教学实践探究

范云

摘 要：数学新授课的教学一般是以学科章节进行，而高三复习课旨在为学生自主构建知识体系，在掌握了一般的章节知识的前提下，将学习内容前后联系，融会贯通，自主整合出解决一类问题的方法和模式，将学习过程从学科章节的学习走向学习单元的整体掌握.在此过程中，可视化的教学工具可以起到很好的辅助作用，帮助学生构建高阶思维，完善认知结构.

关键词：学习单元；可视化教学

高中数学学习内容有一定的难度和深度，学生学习困难的主要原因是学习内容错综复杂，没自主建构知识体系，还停留在老师讲授、自己被动接收的状态.因此，在教授复习课时，教师需要把章节知识重新整合，融合有关联的内容，使得数学教学具备整体性和前瞻性.在此过程中，教师还要注重培养学生自主整合知识以及综合分析问题、解决问题的能力.当学生的探究遇到瓶颈时，需要充分尊重学生的主体地位，可以借助可视化的教学工具，從而激发学生的学习兴趣，同时引导学生积极思考，培养高阶思维，形成自身的知识体系.

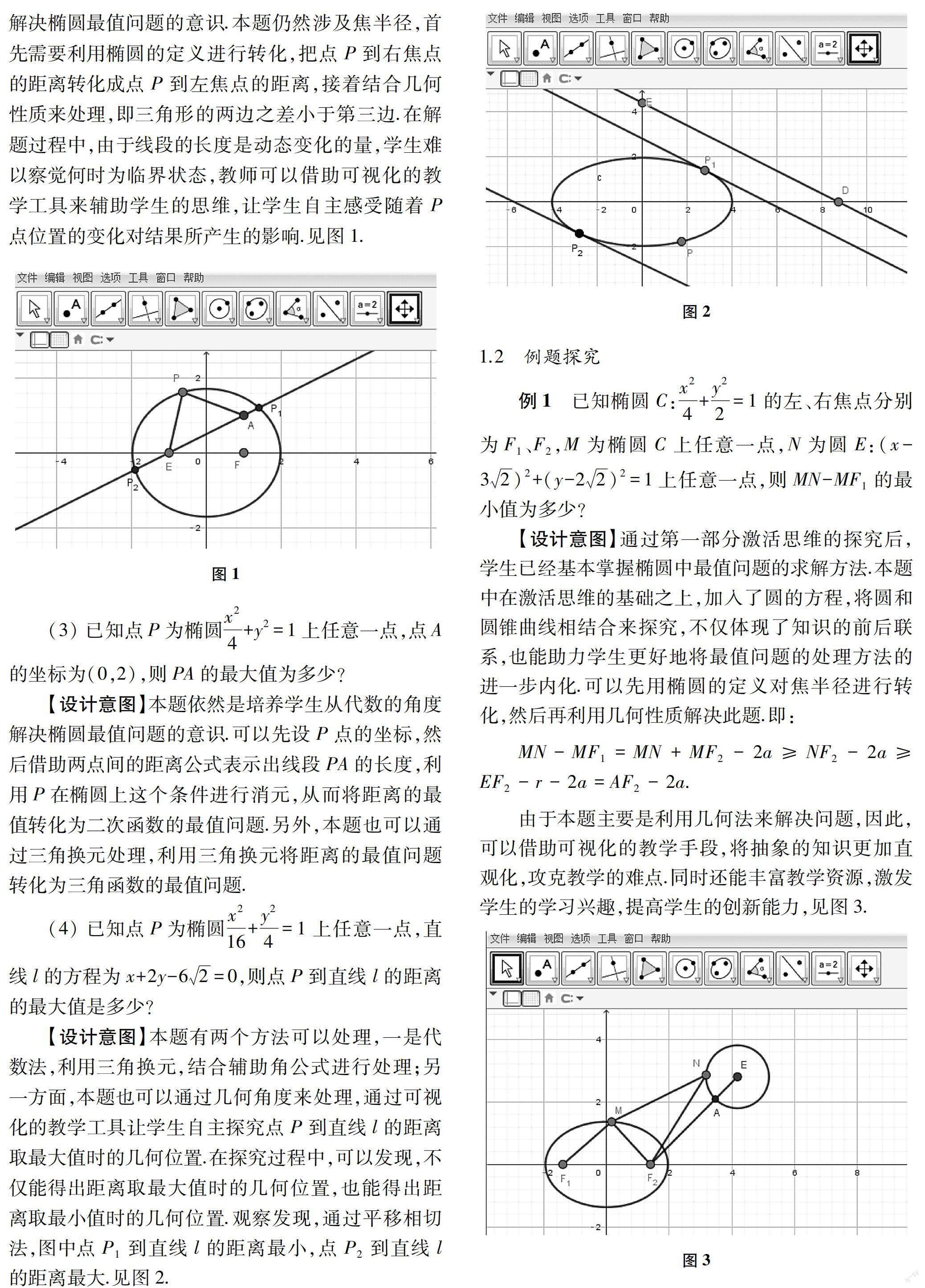
1 实践探究本文以椭圆一章的学习为例，椭圆属于圆锥曲线的一部分，在高考中的考察要求较高，新授课中椭圆的学习章节一般分为椭圆的标准方程、椭圆的几何性质、直线和椭圆的综合应用这三个部分.在复习课时，教师需要更新教学理念，将三个部分的内容进行重新整合，不受章节知识的限制，从中提取出学生学习的难点内容进行归类，比如离心率、定点问题、定值问题等等.其中，最值问题也是难点之一，该问题灵活性、综合性较强，处理起来涉及到章节前后知识点的联动，因此适合进行单元整合教学.

由于最值问题处理起来的难度较大，教师可以引导学生在适当的时候进行可视化探索，利用合适的可视化教学工具更加直观地进行数形结合，突破思维的障碍.常用的可视化教学工具有思维导图、几何画板、GeoGebra软件等等，教师需要对其进行对比分析，选择合适的工具进行使用.由于GeoGebra软件数形结合紧密，功能强大，所以本文在涉及到需要进行可视化的环节选择这款软件辅助教学.以下是“椭圆中的最值问题”一课的教学过程及其设想.

1.3 小结

综上所述，上述最值问题的处理过程中涉及到了椭圆的定义、点和椭圆的位置关系、直线和椭圆的位置关系，这些内容贯穿了整个椭圆章节的学习.如果不进行单元整合，学生学习起来会缺乏着力点，显得知识点非常分散，也难以总结出处理这一类问题的通性通法.因此，在高三复习课中帮助学生重构学习单元至关重要，这是提升学生分析问题、解决问题能力的重要一环.

通过对通性通法的总结探索，可以发现，处理最值问题主要分为两个途径，分别是代数法和几何法.涉及到几何法的探究时，对学生的作图能力、数学抽象能力、直观想象能力要求很高.由于徒手作图的精确性有偏差，另外不能很好地体现动态的变化过程，因此，借助可视化的教学手段，可以更加直观地探究何时取得最值，突破学生想象力的瓶颈，更好地帮助学生自主构建认知结构.

2 总结与反思

2.1 深入研究学习单元，促进高效复习

高中数学知识内容较多，难度较大，学生在学习过程中若不能发现前后联系，并把问题归类处理，就会陷入课堂能听懂，但课后不会解题的尴尬局面.因此，要想实现学生数学能力的突破，老师需要深入研究学习单元的内容，结合新课标的理念，对相关知识点进行有机融合，梳理学生学习过程中会遇到的困难，将困难进行分类，明确教学目标，找到解决一类问题的通性通法.设置教学目标时注重对学生能力的培养，对思维深度的拓展，让学生形成自主的单元学习体系.

2.2 利用可视化手段，丰富教学资源

在传统的数学课堂中，老师轻演示重讲授、轻过程重结果，导致学生自主思考的能力较弱，不利于长远的发展.目前，信息化已经渐渐融入日常课堂教学，数学课堂也是如此.由于数学学习对学生抽象能力要求较高，教师可以利用可视化的教学工具进行辅助教学.

可视化工具很多，老师课前需要做大量的准备工作，厘清不同教学工具之间的区别和联系，选择最适合本堂课教学的可视化工具.需要注意的是，可视化工具的使用上不是越多越好，比如本课中涉及纯代数法的内容并没有进行可视化的展示，因为任何工具在教学环节中都是起辅助作用，当这个环节不需要时，不能强行使用，这样反而会冲淡教学内容，影响教学效果.

可视化工具在教学中的恰当使用可以丰富课堂教学资源，激发学生的学习兴趣，帮助学生更加直观地理解抽象知识，深化解题思路.最终，帮助学生发掘解题规律，提高学习效率.

3 结束语

高三的数学复习课有着时间紧、内容深、难度大的特点.按章节学习已经不能完全满足教学需求.老师需要对教学内容进行重新整合，针对学生学习的难点进行一一突破.注重前后知识的整体性和连贯性，帮助学生解题规律模型化.在学生遇到学习的瓶颈时，借助可视化的教学工具辅助教学，以培养学生的高阶思维，更好地满足当代学生发展的需求.

参考文献：

［1］ 张志勇.高中数学可视化教学：原则、途径与策略——基于GeoGebra平台［J］.数学通报，2018，57（7）：21-24，28.

［2］ 陈雷.深度学习理念下的物理大单元教学［J］.文理导航（中旬），2022（1）：25-27.