做好数学实验 促进概念建构——《三角形的认识》教学

文|程伟伟

【教学内容】

苏教版四年级下册第75、76 页。

【教学过程】

一、激活经验，实验感知

1.寻找三角形，激活经验

师：课前请大家收集资料，寻找生活中的三角形。有几位同学还拍了视频，我们一起来欣赏一下。

生：我佩戴的红领巾是三角形的。

生：我玩的魔方的面是三角形的。

生：我的自行车有一部分是三角形的。

师：老师也收集了一些图片（课件出示四张图片：金字塔、罗马教堂、南京长江大桥、水云阁）。这些建筑物上都有三角形，看来三角形在生活中的应用还真不少！今天我们进一步来研究它。（揭示课题）

2.动手实验，建构概念

（1）初次实验，引发猜想

师：看了这么多的三角形，想不想动手实验？你们可以用身边的材料创造一个三角形，同桌合作。

（2）交流经验，提出猜想

师：介绍一下这些三角形是怎样创造出来的。

生：我用直尺在纸上画了一个三角形。

生：我在钉子板上用橡皮筋围了一个三角形。

生：我用3 根火柴棒摆了一个三角形，摆的时候要注意把小棒连起来。

师：怎样连起来？

生：把火柴棒的头和尾连起来。

师：这种连法叫作首尾相接。

师：这些形状和大小各不相同的三角形都有哪些共同特征？

生：它们都有3 条边。

生：还有3 个角。

师：你们觉得在数学上什么样的图形是三角形？

生：有三条边的图形叫作三角形。

生：我们不同意，有三条边和三个角的图形才是三角形。

师：大家提出了两种不同的猜想，哪一种更合理？在数学上，由几个例子得到的结论只能作为猜想，还需要举出更多的例子去验证。下面请同学们继续探究吧！

（3）实验探究，寻找反例

（学生分小组进行验证实验，教师巡视、指导）

师：有三条边的图形到底是不是三角形呢？有没有找到反例？

生：找到了，我们画的这个有三条边的图形就不是三角形（如下图）。它的三条边是曲线，而三角形的三条边应该是直直的线段。

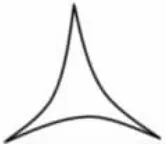
师：这个反例充分说明了第一种猜想是错误的。那有三条线段和三个角的图形就一定是三角形吗？

生：也不一定，我们摆的这个图形就不是三角形（如下图）。

师：是的，一看就知道它不是三角形，第二种猜想也是不成立的。那怎样才能围成一个三角形？

生：（边说边动手修改反例）三角形应该是一个封闭图形，这些火柴棒的头尾依次连起来才能围成一个三角形。

师：同学们很会动脑筋！不仅能找到反例，还能动手修正反例。

（4）交流思辨，建构概念

师：回顾刚才的验证实验，谁能完整地说一说什么样的图形是三角形？

生：三条线段连在一起的图形叫作三角形。

生：三条线段首尾相接围成的图形叫作三角形。

师：（手指着黑板上的三角形）这三条线段就是三角形的3 条边，三条线段首尾相接就形成了三角形的3 个顶点和3 个角。看来，三角形与“3”有着不解之缘呢！

师：再来考考你们。这是三角形的顶点，它的对边在哪？另外两个顶点和对边在哪里？大家伸出手指比划一下。

3.画图反思，拓展概念

师：下面的方格纸上有2 个定点。你能再找1 个点，以这3 个点为顶点，画一个三角形吗？你有什么发现？

（学生独立完成操作，并组织交流汇报）

师：任选1 个点一定能和给定的2 个点画一个三角形吗？

生：不一定，这个点不能和给定的2 个点在同一条直线上。

师：为什么不能？

生：如果这个点和2 个定点在同一条直线上，那么这三条线段就会重合在一起，是不可能围成三角形的。

小结：围成三角形的3 个顶点是不能在同一条直线上的。

二、迁移经验，实验建构

1.初步猜想，感悟高

师：刚才我们认识了三角形，了解了三角形的特征。三角形里还有很多知识等着我们去研究呢！请看（出示下图），长颈鹿迷路了，你能把它送回家吗？

生：因为长颈鹿高，所以高的房子才是它的家。

师：那这座房子有多高呢？

生：从房顶到地面的距离就是房子的高。

师：房子的这个面是三角形（点击课件，去房子，出现三角形），你们觉得什么是三角形的高？

生：三角形的顶点到对边的距离就是三角形的高。

师：其他同学也这么想吗？这只是猜想，我们还需要验证一下。

2.动手实验，概括高

师：（动手演示三种情况）以下哪一条线段可以表示三角形的高呢？为什么？

生：线段①不是高，因为它没有从顶点出发。

生：线段③也不是高，因为它不垂直。

生：线段②是三角形的高，因为它垂直于底边。

师：在小组内讨论一下什么是三角形的高。

生：三角形的顶点到对边的垂直线段是三角形的高。

师：一般情况下三角形的高要画成虚线，并标上直角符号。（课件演示高和底的概念）

师：（课件演示三角形的旋转）这个三角形原来的底在哪？它对应的高呢？观察一下底的方向和高的方向，发生了什么改变？

生：看来底不一定在下面，三角形的高也不一定是竖直方向的，但三角形的高一定是从顶点向对边作的垂直线段。

3.联系旧知，理解高

师：同学们真了不起，能找准对应的底和高。想不想动手画一条高？

师：别急，我们先来看看怎么画高。（课件演示）

师：学会了吗？（出示题目）现在以这条边为底，谁想上来试一试？其他同学在作业纸上画。

师：其实，像这样画高的方法我们早就学过了，请看大屏幕，想起来了吗？（课件演示点到直线的画法）

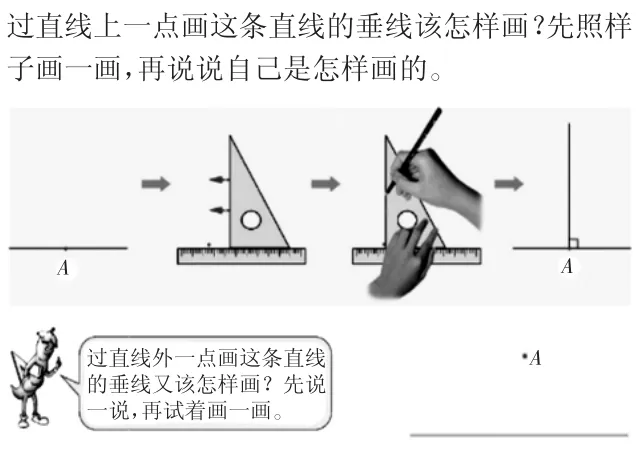
生：画高本质上就是四年级学过的画直线外一点到这条直线的垂直距离。

师：你们真厉害，立马能把以前学过的知识迁移过来。如果把三角形的底边看成一条直线，那直线外一点在哪？就是三角形的顶点。从直线外一点向这条直线画的垂直线段就是三角形的高。

师：刚才我们以这条边为底画出它的高，那三角形只有一条高吗？

生：不，三角形有3 个顶点，所以它有3 组对应的底和高。

三、变化实验，建构关系

1.画一画：画出下面三角形底边上的高。

师：观察这四个三角形底边上的高，你有什么发现？

生：前三个三角形是锐角三角形，它们的高在图形内部，第四个是直角三角形，它的高是另一条直角边。

师：观察得真仔细！三角形的高有的在图形内部，有的在边上，还可能在哪？

生：三角形的高还可能在图形外部。

师：这仅仅是我们的猜想，需要验证一下。

2.变一变：方格纸上有2 个点，再找1 个点，画一个高是3 厘米的三角形。

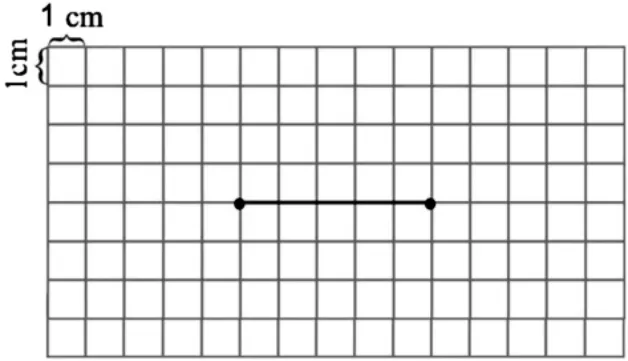
师：你能找到几个这样的点？你能画几个这样的三角形和高？你有什么发现？

生：可以找到无数个这样的点，画出无数个高是3 厘米的三角形。

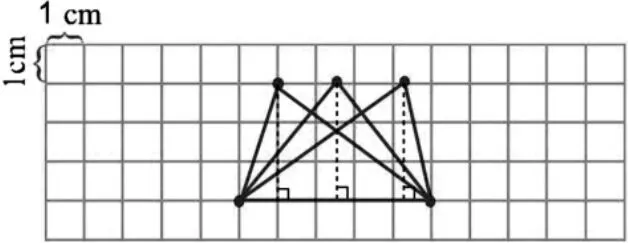
师：仔细观察这些三角形和它们的高，你们有什么发现？

生：这些三角形底一定，高也一定，但形状却不相同。

生：这些三角形底的位置不变，但是高却随着顶点慢慢地向右移动。

（教师利用几何画板动态演示，顶点沿着底边的平行线逐渐向右移动，底边上的高也随之向右移动，直至与直角边重合的情况）

师：如果顶点继续向右移动，这个三角形的高将会发生怎样的变化？（教师边说边继续演示高出现在三角形外的情况）

生：三角形的高可能在图形内部，可能在直角边上，还可能在图形外部。

师：通过实验验证，发现我们刚才的猜想是正确的。那这个点只能在上面吗？

生：还可以在下面。

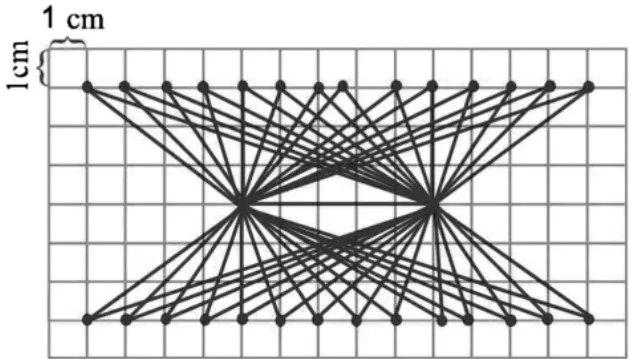
师：在数学上，我们把这样的三角形叫同底等高的三角形。

四、回顾反思，结构延伸

师：通过开展数学实验，你对三角形有哪些新的认识？我们是怎样研究三角形的特征和高的？你又有哪些体会和收获？