如何说明对数的存在性与唯一性?——从一线教师对沪教版教材的困惑谈起*

李 卓 魏 梦 (江西师范大学数学与统计学院 330022)

从2020年秋季学期起,上海开始使用上海教育出版社出版的高中数学新教材(以下简称新教材)．伴随着新教材的使用,上海各个区都开展了关于高中数学新教材的教研活动．应M区高中数学教研员Y老师的邀请,研究者参加了M区高一新教材对数定义的教研活动,在研讨交流环节有几位一线教师都提到了新教材中对数相关内容的编排方式及其带来的困惑.在与Y老师交流后,我们试图通过对教材的研读来回应并消解一线教师的困惑．下面首先介绍新教材中运算与函数相对独立的编排方式;其次梳理这种编排方式给一线教师带来的困惑;然后尝试回应并消解一线教师的困惑;最后厘清新教材采用这种编排方式的原因．

1 新教材的编排方式

旧教材将对数与对数函数合并在同一章节(图1),新教材明确区分“运算”与“函数”将“幂、指数与对数”作为独立的一章(图2),放在“幂函数、指数函数与对数函数”一章之前．

图1 旧教材的编排方式 图2 新教材的编排方式

2 一线教师的困惑:新教材很难说明对数的存在性与唯一性

在教研活动的研讨交流环节,一线教师提出了以下有代表性的困惑:

赵老师的困惑:旧教材的编排方式是指数函数→对数→对数函数,指数函数在对数的前面,按照旧教材的编排方式,ax=N中x的存在性与唯一性可以利用指数函数说明;新教材的编排方式是对数→幂函数→指数函数→对数函数,指数函数放在了对数的后面．按照新教材的编排方式,在讲对数时,很难说明ax=N中x的存在性与唯一性．其中,唯一性可以用反证法证明,但是存在性不能证明,而存在性是唯一性的前提,先有存在性才能有唯一性,先说明存在性才能证明唯一性．

钱老师的困惑:在使用旧教材时,对于ax=N这个方程,它的解是否是存在且唯一的是由指数函数来保证的．现在在使用新教材讲对数时没有指数函数了(这位教师表达的意思是:新教材把指数函数放在了对数的后面,高一学生在学习对数的时候还没有学习指数函数),很难说明ax=N这个方程的解x是存在的而且是唯一的．

赵老师和钱老师谈完自己的困惑后,其他教师也纷纷表示有类似的困惑．

在实际课堂教学中,很多一线教师采用了赵老师和钱老师提到的用指数函数图象说明ax=N这个方程的解x是存在且唯一的[1-3]．例如南京师范大学附属中学张萍老师在说明x存在唯一时便是利用指数函数[1]．教学实录如下:

师:2b=3,这样的指数b有没有呢?

生:2b=3这个问题和指数函数y=2x有关,我们可以作出它的图象来观察．

师:作出y=2x与y=3的图象(图3),发现它们有交点,且只有一个,那么指数b在哪里呢?

图3 y=2x与y=3的图象

生:交点的横坐标就是指数b．

师:看来满足2b=3的指数b唯一确定．

用反证法可以证明唯一性．

求证:方程ax=N(a>0,且a≠1)总有唯一的解．

②测PH值法：取等浓度的二种溶液各少许，分别测其PH值，PH值大者N a2CO3，PH值小者 N aH CO3；

又x1-x2>0,根据幂的基本不等式及其推论(图4):

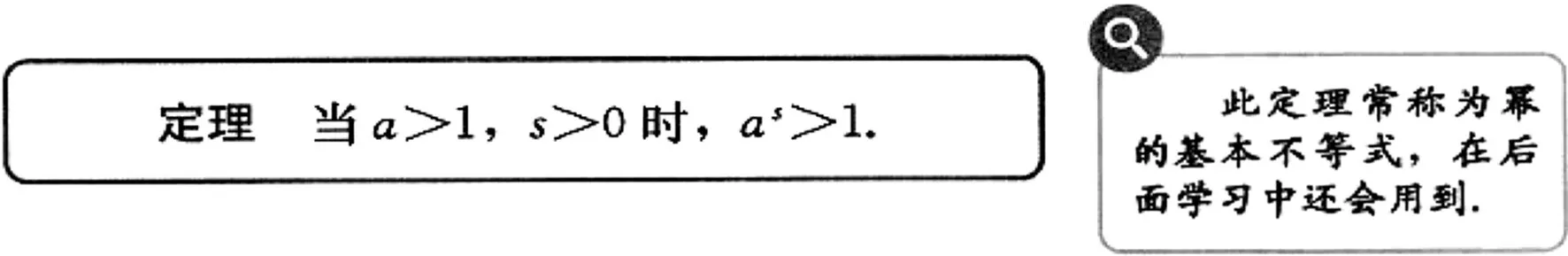
图4 新教材中幂的基本不等式

当a>1时,ax1-x2>1,与ax1-x2=1矛盾;

当0

所以假设不成立,即方程ax=N(a>0,且a≠1)总有唯一解．

3 从惑到识:高中数学新教材很难说明对数的存在性与唯一性吗?

针对ax=N中x的存在性与唯一性,新教材的配套教参是这样写的:

本研究从存在性和唯一性出发,在a>0的条件下,说明这是使方程ax=N存在唯一解所应满足的条件．教学中虽应说明这部分的内容,但是要把握好度,对存在性和唯一性不必证明,只需直观了解即可．

由此可知,教师在教学中可以以直观的形式向学生说明ax=N中x的存在性与唯一性．

x122x24

比如取指数为1.5,用计算器计算知21.5=2.828,由于2.828比3小,就把指数再变大一点,重复这个过程就可以找到一个指数x0,使得 2x0=3．上海交通大学附属中学陶磊老师便是采用了类似的做法[4]．教学实录如下:

师:10x=2 018,这样的指数存在吗?

生(部分学生):存在．

师:你们觉得存在,好像有人没有回答,可能还有点不知道应该怎么说．那我们大概估算一下,你觉得存在的话,这个x大约是多少?10的多少次方,3次方好像小了一点,4次方好像大了一点,差不多3到4之间．那我在3到4之间列个表,看看这个表,x大约在哪?

x3.13.23.33.43.53.63.73.83.9410x1 258.91 584.91 9952 5123 1623 9815 0126 3107 94310 000

生:3.3到3.4之间．

师:非常好,好像还是不够精确是吧．如何寻找更精确的一点呢,还可以怎么样?

生:细化．

师:很好,你们用的词很好,细化．说得非常形象,那这回呢?大约在哪?

x3.3013.3023.3033.3043.3053.30610x1 999.861 92 004.4722 009.092 013.722 018.372 023.02

生:3.304到3.305之间．

师:3.304到3.305之间,可以想象如果我不断地细化,我总能找到近似值．

高中数学课程标准修订组组长、原东北师范大学校长史宁中教授指出:“无论是教材的编写,还是教学的设计,都可以考虑改变传统的设计思路,不是对每一节课或每一个知识点进行设计,而是把一些具有逻辑联系的知识点放在一起进行整体设计．把这些内容前后照应进行教学设计,就可以在关注知识技能的同时,思考知识技能蕴含的数学本质、体现的数学思想,最终实现学生形成和发展数学核心素养的目标[5]．考虑到对数部分ax=N中x的存在性与唯一性和指数函数之间的逻辑联系,在讲ax=N中x的存在性与唯一性时,教师可以在举例的基础上简单提一下:后续学习指数函数之后可以更进一步明晰ax=N中,x为什么是存在且唯一的;讲到指数函数的时候再用上文赵老师、钱老师提到的用指数函数的知识进一步说明ax=N中x的存在性与唯一性．

为什么新教材的配套教学参考书说明对存在性和唯一性不必证明,而只需直观了解即可呢?我们认为主要是因为在高中阶段无法严谨地证明ax=N中x的存在性与唯一性．因此我们认同新教材编写人员的观点,教学中只需让学生能够体会到ax=N中x是存在且唯一的即可．

此外,我们认为不宜采用赵老师、钱老师提到的用反证法证明ax=N中x的唯一性．因为证明过程中,会用到幂的基本不等式．而新教材引入幂的基本不等式的目的是为了后面证明幂函数、指数函数和对数函数的严格单调性,并不是为了证明ax=N中x的唯一性

4 追根究底:高中数学新教材为什么要采用运算与函数相对独立的编排方式?

一线教师的困惑主要是新教材的编排方式带来的,因此有必要搞清楚为什么新教材要采用运算与函数相对独立的编排方式．新教材主编之一、原华东师范大学校长王建磐教授在新教材培训时是这样解释的:运算与函数相对独立,桥归桥路归路．新教材把“幂、指数与对数”作为独立的一章(第3章),出现在“幂函数、指数函数与对数函数”一章(第4章)之前,把“三角”作为独立的一章(第6章),出现在“三角函数”一章(第7章)之前,把“运算”与“函数”明确区分,在运算上能下足功夫,讲清来龙去脉．也就是说,采用新的编排方式,运算讨论的就是运算性质等,函数讨论的就是纯粹的函数,包括函数的定义、函数的图象与性质等,这样学生的认知结构中对于函数的概念应该是非常清晰的．