初中数学单元整体教学设计策略初探

石礼芹 (江苏省淮安市金湖县教师发展中心 211600)

《义务教育数学课程标准(2022年版)》指出:“要改变过于注重以课时为单位的教学设计,推进单元整体教学设计,整体分析数学内容本质和学生认知规律,合理整合教学内容,促进学生对数学教学内容的整体理解与把握,逐步培养学生的核心素养．”[1]著名教育家陶行知先生说过:“我以为好的先生,不是教书,不是教学生,乃是教学生学”．单元整体教学提倡“通过结构化的长程设计,帮助学生建立清晰的知识结构并获得研究问题的方法．”这正是一种“教学生学”的教学方式．

笔者对基于整体观的教学曾做过一些尝试．关于单元整体教学的意义和价值,课标和众多文献已有较深入的阐述,在这里不再赘述,现将笔者在“单元整体教学设计”方面的所学与所想整理出来,与大家共享．

1 单元整体教学设计的常用策略

单元整体教学要求教师全面把握教材,厘清教学内容之间的联系,这种联系可以是不同单元知识在学习路径、研究方法上的一致性,也可以是同单元知识在新知生长点、逻辑关系等方面的关联性．以此为基础,可以选择不同策略进行单元整体设计．本文结合5个案例,谈一谈单元整体教学设计的常用策略．

1.1 侧重从新旧知识之间的联系入手进行单元整体教学设计

策略一 沿袭学习路径进行单元整体教学设计

数学知识是相互联系的,许多知识虽然分布在不同的年级、章节和单元中,但它们在知识结构上存在着相似性,这样的新知可以沿袭旧知的学习路径展开单元整体教学[2]．

案例1苏科版教材(下文所涉及的内容均出自苏科版教材)八年级下册“9.3 平行四边形的概念、性质和判定”．

由于它的结构与“等腰三角形的概念、性质和判定”高度相似,所以可以沿袭以往的学习路径进行单元整体教学．设计如下:

先请学生回顾等腰三角形的学习路径(图1):

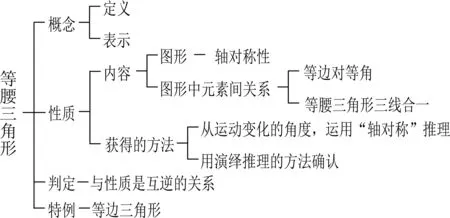
图1 等腰三角形的学习路径

类比出平行四边形的学习路径(图2):

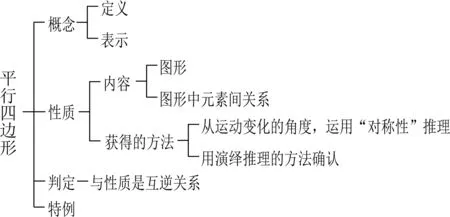
图2 平行四边形的学习路径

虽然平行四边形与等腰三角形分属两册教材,但它们的知识结构相似,都是“概念—性质—判定”,所以沿袭等腰三角形的学习路径进行本节内容的单元整体设计,会使教与学的思路都更加清晰,易于学生探究并获得结构化的知识．

策略二 借鉴研究方法进行单元整体教学设计

章建跃博士指出:“数学应有一套具有普适性的思考结构．”[3]这里的“普适性的思考结构”就是研究问题的思路和方法．许多新知识的学习不需要全新的尝试,是有现成的方法可以借鉴的．

案例2九年级下册“5.2 二次函数的图象和性质”．

一次函数、反比例函数是学习二次函数的基础.为使新旧知识有更密切的衔接,在教学“一次函数图象和性质”时,改变教材中的研究顺序,从特例y=2x和y=-2x入手,先“由数想形”画出图象,再“由形思数”明晰它们的性质,然后概括出正比例函数y=kx(k≠0)的图象和性质,继而将y=kx(k≠0)的图象进行上(下)平移,探索一次函数y=kx+b(k≠0)与y=kx(k≠0)在图象特征和函数性质方面的联系与区别．整个探究过程应用的主要研究方法是数形结合、有序分类和由特殊到一般．

二次函数的图象和性质可以借鉴这个研究方法,从特例y=x2和y=-x2开始,用“数形结合”和“有序分类”的方法得到它们的图象与性质,再“一般化”概括出y=ax2(a≠0)的图象与性质,继而通过将y=ax2(a≠0)的图象平移,探索y=ax2+c(a≠0)的相关知识．在小结时,引导学生推想:若将y=ax2(a≠0)的图象向左(右)平移,或先向上(下)、再向左(右)平移,得到的函数的图象和性质将如何研究?

这里将研究方法“明示”给学生(图3),在教学环节的推进过程中让学生感受研究方法的普适性．

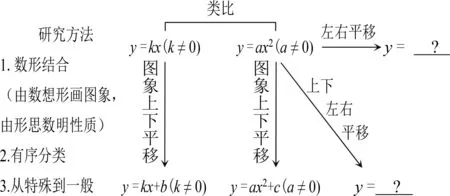
图3

奥苏伯尔说:“有意义学习就是将新知识与已有知识建立起非人为(内在)的和实质性的联系．”以上两个案例就是引导学生进行有意义的学习,在新旧知识联系的过程中,感受学习路径和研究方法的可复制性．在这样的学习中,学生们普遍感到学习的难度降低了,效率提高了,对数学知识的整体性印象变得深刻了．

1.2 侧重从新知识内部的联系入手进行单元整体教学设计

有一些知识与前面章节的联系不太紧密,而本单元内知识之间却有独特的关联性,像这样的内容可以因课而异,选用不同策略开展单元整体教学．

策略三 设置恰当情境,以点带面

案例3九年级下册第7章“锐角三角函数”中“7.1 正切”“7.2 正弦、余弦”．

本单元的两节内容有两个共同点.一是它们(sinA,cosA,tanA)都以实际问题为背景,学生可以从已有知识出发探索并认识它们;二是它们的本质属性相似:直角三角形中,某两边的比值随锐角度数的变化而变化,当这个锐角的度数确定时,这两边的比值有唯一的值与其对应．对于这样的内容,可以设置恰当情境,围绕核心问题,以点带面进行单元整体教学．福建省永春华侨中学谢雅礼老师的做法如下[4]:

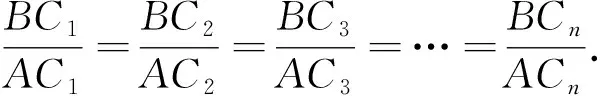
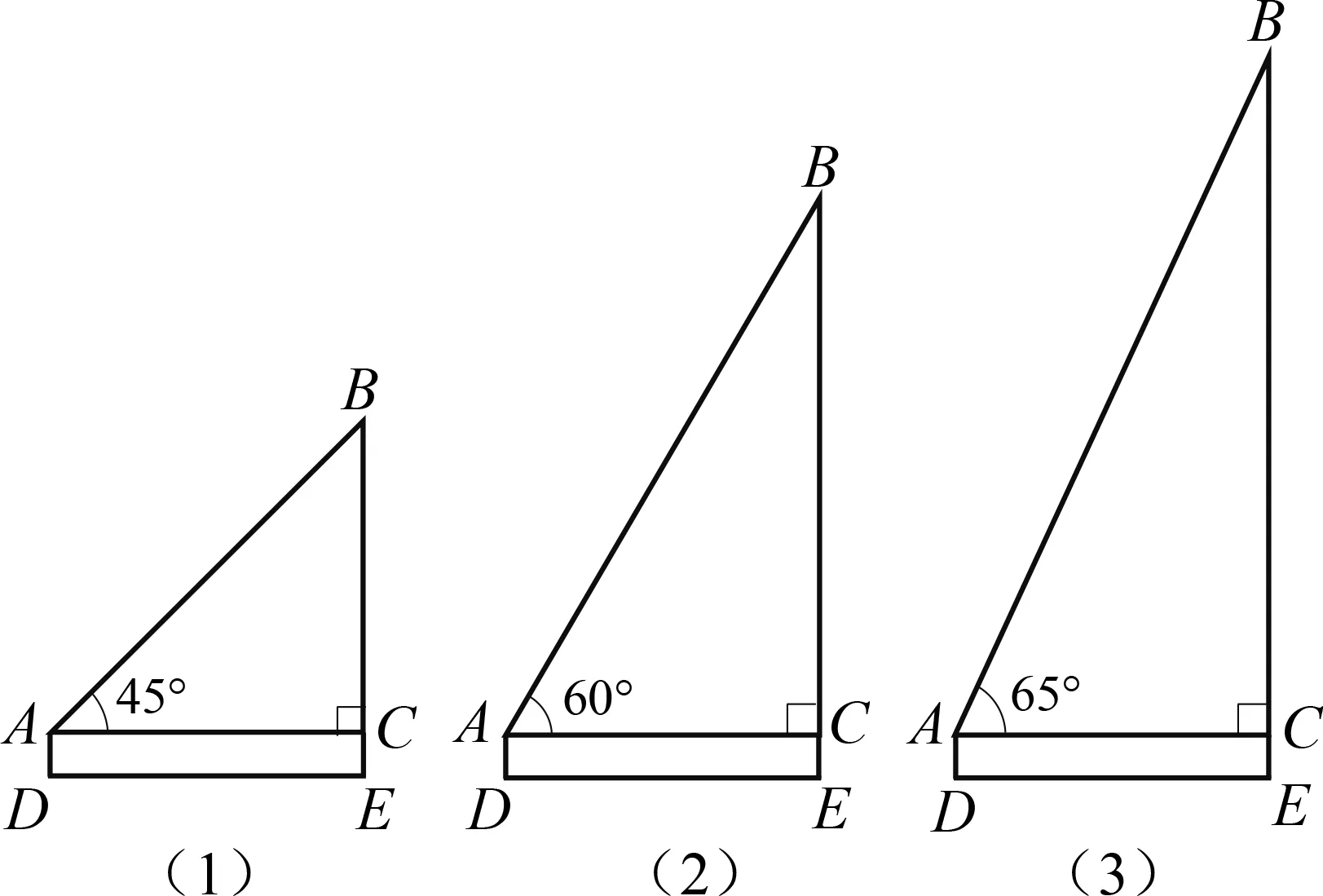
图4

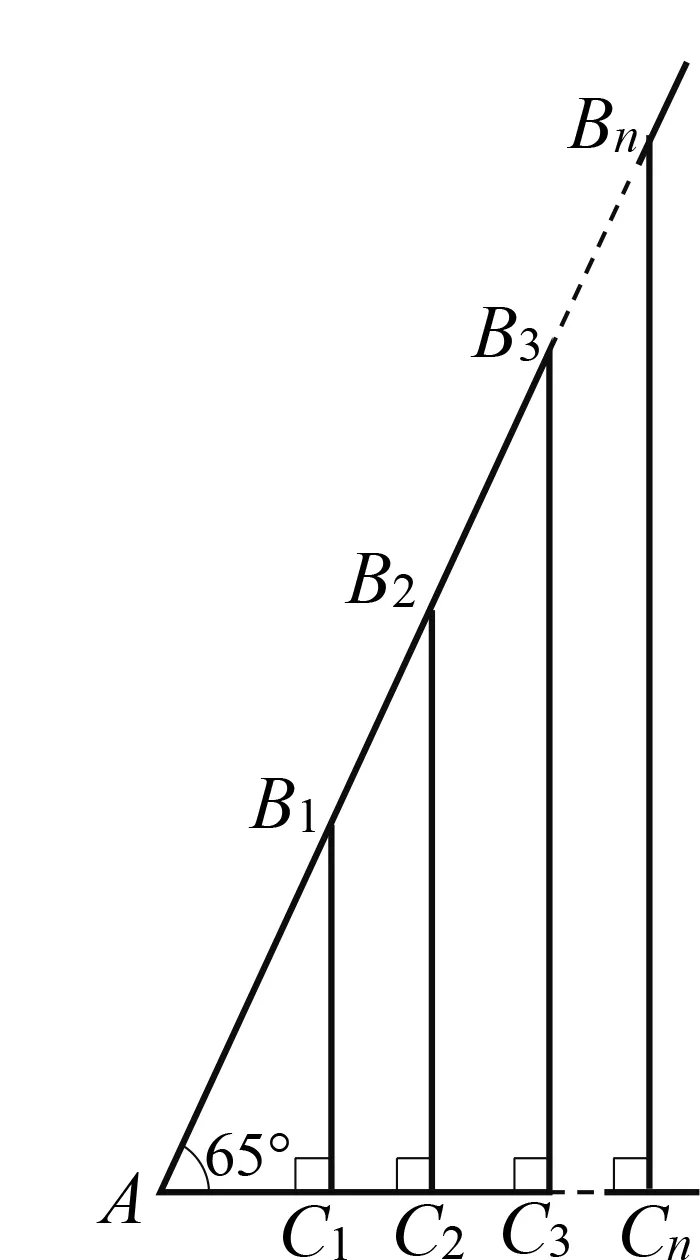
图5

本案例中教师设置恰当情境,引出一个核心问题:在∠A=65°的直角三角形中,a与b的比值是否为定值?教学过程中学生围绕这个核心点进行探讨,他们积极参与,举一反三;教师则以点带面,层层推进,使学生顺利领会了本章要学习的锐角三角函数概念．这样的设计不但让学生感受到知识的整体性,还培养了学生的推理能力和应用意识．

策略四 寻找生长基点,串珠成线

数学中很多新知识都是在同一个旧知的基础上“生长”出来的,找准这个“生长点”,就可以将这部分知识串珠成线进行单元整体教学设计．

案例4七年级下册第8章“幂的运算”中“8.1 同底数幂的乘法”“8.2 幂的乘方和积的 乘方”．

研读这几节的内容会发现,“乘方的意义”就是本章学习的生长点．可以设计以下环节,展开本节单元整体教学．

环节1 出示教材中8.1节的引入题,列式后讨论108×102的计算方法．在此环节中,注意引导学生回到乘方的意义中去明晰算理．

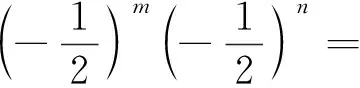
环节3 分两个步骤进行．(1)练习巩固:做教材中的练习题,巩固同底数幂乘法的运算性质．(2)提问:“底数a还可以表示什么,你能不能编出不同的题?”这个问题有开放性,学生可能会有多种答案,如底数为多项式、底数为乘积式、底数为幂的形式;教师因势利导,引导学生用整体思想理解掌握形如(a+b)m(a+b)n(m,n是正整数)这类题目的计算方法,重点讨论形如(ab)n(n是正整数),(am)n(m,n是正整数)这类题目的运算性质．

可以看出,“同底数幂的乘法”的运算性质依据的是“乘方的意义”;积的乘方(ab)n(n是正整数)的运算性质依据的也是“乘方的意义”;幂的乘方(am)n(m,n是正整数)的运算性质可以依据“同底数幂的乘法”,也可以直接依据“乘方的意义”获得．可见,“乘方的意义”是这些知识的生长点,围绕它展开整体教学,在知识的自然生成中完成整体教学,使得数学学习变得简洁又清楚．

策略五 顺应发展过程,逐步推进

数学知识是逻辑连贯的,可以顺应知识的发展过程,采用一脉相承、逐步推进的方式进行单元整体教学设计．

案例5九年级上册“1.2 一元二次方程的解法”．

教材中安排了四种解法的教学任务,分别是直接开平方法、配方法、公式法和因式分解法．整体分析教学内容,可以发现前三种方法是紧密联系的:配方法是将一元二次方程配方后,直接开平方求解;求根公式是先将一元二次方程的一般式进行配方,再用直接开平方法获得方程的解．可见,直接开平方法是解一元二次方程的起点,配方法以直接开平方法为基础,公式法以配方法为基础．从直接开平方法到配方法再到公式法是顺次渐进的过程．这部分内容可以设计如下问题串逐步推进教学．

问题1:求一元二次方程ax2+bx+c=0 (a≠0)的解,我们一般从最简单的特例出发开始研究,尝试解x2=1,依据是什么?

问题2:解(x-2)2=1,这里体现了什么思想?

问题3:你会解x2-4x=5吗?可以从上面的式子中受到什么启发吗?如果是2x2-8x=7呢?

问题4:你能尝试解ax2+bx+c=0(a≠0)这个方程吗?

从问题1到问题4的设计顺应知识的发展过程,让学生在知识的层层推进中,充分理解一元二次方程ax2+bx+c=0(a≠0)的解法:起点是直接开平方法,最终落脚于公式法,感受数学知识的逻辑连贯性;同时也让学生感受到数学强大的简化功能:以一个有限的模式(求根公式)驾驭无穷的具体(各个一元二次方程),体会数学的逻辑美、统一美和简洁美．

2 单元整体教学设计要注意的几个问题

2.1 要注意实施的适切性、灵活性

单元整体教学的目的是在高立意下,帮助学生学会用整体的、联系的、发展的眼光看问题,形成对知识的整体化、结构化的认识．但在实施的过程中,教师要注意适切性,做到区别对待:对于认知水平和学习基础好的班级,可以一步到位;对于学习基础比较薄弱的班级,则要灵活运用、分步实施．

如案例2,在基础薄弱的班级实施教学时,不宜按原来的计划同步教学,要放缓节奏.可以按照课标中“整体设计,分课时实施”的建议,将此设计按照教材中的编排体系细分为三个课时:第一课时,要复习一次函数的图象与性质的研究方法,注意将“从最特殊的开始研究”这种思路和“由数想形”的方法渗透给学生;第二课时,要重点将“由数思形”、分类讨论的思想渗透给学生;第三课时,在有关一次函数的复习活动中,引导学生回忆起从“特殊”到“一般”的研究思路和方法,进而领会探索y=ax2+c(a≠0)等函数的图象和性质可以y=ax2(a≠0)的图象和性质为基础和起点．虽然内容拆分开来了,但它们是在整体教学设计思想的统领之下展开的.随着教学任务的顺次完成,对教学内容的整体理解和把握得以分步落实．

2.2 要提炼并展现结构化的板书

结构化的板书有利于让学生获得结构化的认识．由于单元整体教学重视知识的结构化,注重知识的关联、方法的迁移,所以与之配套的板书也要相应地结构化．首先,注意知识的整体性．要将分散的知识进行整体加工,做到串珠成线、连线成网,帮助学生建立较完整的知识体系．其次,要注意将研究方法等“明示”给学生．“教学生学”就要将研究思路、研究方法、解题思想等通过板书“有痕”地展示给学生,帮助他们积累经验,使他们在学习新知时有方法可借鉴、有思路可沿袭,让主动学习成为可能．如前文中图2、图3所示,结构性越强的板书对学生的视觉冲击力越大,及时将它们展现给学生,更容易在学生的大脑中形成完整的知识网络,也有利于思路和方法的类比迁移．

2.3 要发挥小结的梳理回顾作用

做单元整体教学课堂小结时,不仅要对本课知识进行小结,更要站在整体观的角度,引导学生对新旧知识的结构联系、路径迁移、方法借鉴等加以小结．在零碎信息的梳理中,形成系统的知识网络;在研究方法的回顾中,积累数学研究的活动经验．此环节中,教师可以设计如下问题:

(1)本节课上你学到了哪些知识?

(2)本节课让你感受最深的是什么?

(3)本节课的哪些研究思路对你今后学习有帮助?

(4)课后准备对哪些方面进行进一步研究?

(5)对自己的表现是否满意?还有哪些困惑?

学生可以选择上述问题中感兴趣的话题,反思本节课的学习．其中,问题(3)(4)具有延伸性,有利于培养学生用类比迁移的方法研究新问题的意识．

3 结语

课标指出:“通过合适的主题整合教学内容,帮助学生学会用整体的、联系的、发展的眼光看问题．”可见,进行单元整体教学既是学生发展的需要,也是课标的要求．那么究竟如何整合教学内容?如何选择单元整体教学设计策略呢?这是一个见仁见智的问题．总之,进行单元整体教学设计时,教师要整体把握教学内容,厘清逻辑关系,找到新旧知识的联结点,找准问题研究的切入点,在宏观把握、高位立意的基础上,选用合适的策略进行精细化的设计,以帮助学生建立能体现数学学科本质、对未来学习有支撑意义的结构化的数学知识体系和学习经验．