依托CiteSpace,实施高效备课——以“弧度制”为例*

吴京霖 石义娜 王宽明 (贵州师范大学数学科学学院 550025)

1 问题提出

备课通常是指教师在上课前的教学准备,主要包括备教材、备学生和备教法三个环节[1]．教师通过对教材、课标的深入分析,结合学生的学情特点,选择合适的教学方法,可以有效促进学生对知识的理解．然而在教学实践中,通过上述三个环节的备课,教师虽然可以解决“教什么”和“怎么教”的问题,但对“为什么教”这一问题却关注不多[2]．一方面,教师对课程标准、教材进行分析,可以有效把握教学目标,确定教学内容和教学重难点,但教材由于篇幅、结构的条件限制,往往无法呈现“为什么学”的内容．如在弧度制的引入中,尽管课标在案例中给出了弧度制引入的必要性在于角度制不能运算和角度制无法描述更为一般的周期性现象[3],但在教材中仅以“下面介绍在数学和其他科学研究中经常采用的另一种度量角的单位制——弧度制”来引入．如果教师按照教材的内容进行备课,就会缺乏对“为什么教”的思考.而如果教师借鉴课程标准中案例“弧度制引入的必要性”来揭示“为什么教”,又会陷入该如何有效组织课程内容的困境．另一方面,中学数学教师还需要完成作业批改、班级管理、家校沟通、行政工作等内容,备课时间有限,仓促之余,只能随便应付,敷衍了事,从而导致了同一教学内容的教学设计千人一面[4]．《普通高中数学课程标准(2017年版)》(下称《标准2017》)中指出,不仅要求学生能够应用知识,更要把握数学知识的本质[5]2-3．在这个要求下,传统的备课方式的核心弊端显而易见,其根本原因在于缺乏对教学研究现状的把握．“见贤思齐焉,见不贤而内自省也”,如果教师能够在备课时充分了解诸多同仁对教学知识该如何教学的见解,就可以形成自己的思考,设计出凸显数学本质、促进学生核心素养发展的教学内容．

2 教学研究现状概述

2.1 教学研究现状的内涵与价值

研究现状是指研究群体针对某一问题或情境所做研究的整体情况.在科研任务中,把握研究现状可以有效把握研究进展和不足,为创新研究奠定基础[6]．教学研究现状则是教师们对教学内容中核心问题的理解,包括教学目标、教学重难点、教学理念、问题情境等内容．把握教学研究现状,一方面可以提高对教学内容的认识,真正落实“为促进学生核心素养而教”．如张琦老师通过对“弧度制”一节的教学现状进行梳理,发现不同教学设计的优点和不足,并结合多版教材中对弧度制的引入方式进行思考,最终以单位圆为依托,设计出凸显弧度制本质的数学课堂,获得了较好的教学效果[7]．另一方面,科研型教师已成为21世纪教师的基本要求,而成为一名科研型教师,其基本功就是能够对当前研究成果进行有效梳理,发现前人研究的不足,落实创新研究[8]．

2.2 教学研究现状的梳理途径和困境

在我国,教学研究成果的获取主要有两种途径:一是通过各学术杂志发表的纸质期刊,二是通过中国知网、维普、万方等数据库获取电子文稿．就中学教师而言,纸质期刊的获取要远比电子文稿简单,主要是因为学校一般会统一订阅一些较为经典的数学教育类杂志,如《数学教育学报》《数学通报》等,但这种方法存在两个弊端:一是由于订阅的杂志有限,教师获取某一教学内容的相关文献不全,难以形成对该教学内容的教学研究现状的整体认识;二是教师需要逐篇阅读所搜集到的所有文献,这一过程需要耗费大量的时间和精力．电子文稿可以通过数据库进行主题检索获得,故相对于纸质期刊而言,检索到的文献较为全面,但庞大的数据量容易让中学数学教师望而却步．如在中国知网以“弧度制”进行主题检索,共获得600余篇文献,在短短的1～2个小时内把握这么多文献的研究内容对教师而言是一个极大的挑战．

2.3 基于CiteSpace的可视化文献梳理

为了解决纸质期刊文献不全和电子文稿梳理难度大这两个问题,引入CiteSpace软件作为梳理文献的辅助工具,可以从海量的文献中快速获得研究领域的热点主题,帮助教师在短时间内把握教学研究现状．CiteSpace是由美籍华人陈超美教授开发的一款文献计量学软件,主要通过关键词、参考文献的共现或共被引关系构建知识图谱,以发现研究领域的热点主题和研究前沿[9]．由于梳理教学研究现状与标准的文献综述不同,重点梳理三个方面:一是寻找该教学内容基本问题的观点,如“弧度制”的基本问题就是如何让弧度制的引入变得自然;二是寻找与该内容适配的教学理念;三是寻找具备创新性的教学设计案例．因此,在使用CiteSpace进行分析时,仅需要对关键词分析即可.通过CiteSpace构建关键词共现知识图谱,一方面可以把握当前教学研究中有哪些主要的关键词及与之联系紧密的关键词,从而对教学研究现状有一个整体性的把握,另一方面还可以通过对关键词所对应的文献摘要进行查看,判断该文献是否对我们想要解决的问题有帮助,进而决定是否需要进行全文的深入阅读．

3 基于CiteSpace的“弧度制”教学研究现状梳理

下面以“弧度制”为例,说明如何通过CiteSpace进行教学研究现状的梳理．之所以选择弧度制,是因为弧度制引入的必要性是当前教学研究中颇有争论的一个话题,诸多学者进行了广泛的讨论和探索,研究内容较为驳杂,通过传统的文献梳理方式难以为继．而借助CiteSpace,可以较为快速和准确地把握其主要观点,发现重要文献,帮助数学教师在短时间内形成系统的认识,实现高效备课．

3.1 数据收集与处理

在中国知网以“弧度制”进行主题检索,为了尽可能多地获取相关文献,不做其他检索条件限制,共获得629篇文献．需要注意的是,在标准的CiteSpace分析中,通常需要对文献数据进行筛选,但由于教学研究现状的现实背景是教师需要在短时间内获得基本问题的观点、教学理念和教学设计案例,属于探索性的CiteSpace分析,故是否对数据进行筛选对研究结果影响不大,而且数据筛选通常需要大量时间,所以不对文献数据进行筛选．在检索完成后,通过知网的批量勾选功能将所有文献选定,并以refworks格式导出.由于中国知网的导出数据限制为每次最大500篇,所以需要对629篇文献分批次导出．

获取数据后,将导出的文本数据放入CiteSpace对应的工程文件夹中的input文件夹,并使用数据转化功能将数据转化为wos数据格式．完成后在CiteSpace界面创建工程,并做如下设置:节点类型选择为Keywords;节点选择器为topN(N=50,e=2);为了让图谱更清晰,还通过pathfinder算法对共现网络进行裁剪．在完成上述设置后,即可点击运行,CiteSpace将自动处理数据并生成关键词共现知识图谱(图1)．

3.2 关键词共现知识图谱的基本分析

CiteSpace的可视化界面如图1所示,图谱左侧为关键词的具体信息,包含关键词的频次、中介中心性、首次出现年份等;图谱右侧为关键词共现图,其中上方的颜色谱与时间区间相对应,颜色越深,说明对应的时间越早,颜色越暖,对应的时间越近;在图谱中,节点的大小与频次呈正相关．此外,若节点外部有紫色光圈标注,则说明这些节点的中介中心性不小于0.1,是图中的枢纽节点．

图1 “弧度制”关键词共现知识图谱

由图1可以作出如下基本的判断:一是从频次的角度看,与弧度制最相关的关键词是三角函数、高中数学、任意角、教学设计、圆心角、弧长公式等关键词,体现了弧度制教学研究的主要内容;二是从中介中心性的角度看,处于枢纽位置的关键词有任意角、三角函数、三角函数值、单位圆、定义域、几何画板等,体现了弧度制教学研究的关键

所在;三是从关键词的分类上看,可以发现弧度制教学研究中主要运用的教学理念有深度学习、问题驱动、数学文化、数学史、APOS理论、单元教学等;最后,教学主要运用的信息技术软件是几何画板,而新人教版数学教材中提及的GeoGebra较少运用．

3.3 “弧度制”教学基本问题的探索性分析

通过对《标准2017》和教材的研读,可以确定“弧度制”这一节内容的教学难点是为什么要使用弧度制,即如何让弧度制的引入变得自然．而图1中仅展示基本的关键词信息,无法解决这一基本问题,故还需要通过CiteSpace中的节点信息功能进一步探索．通过点击节点“弧度制”的中心,右键菜单中选择节点细节(Node Detials),弹出页面后选择The Keyword Appeared in N Records,即可获得含该关键词的文献列表(图2)．此时点击到具体文献,即可在下方查看该文献的具体信息,如标题、作者、摘要等,快速判断该文献能否帮助我们理清“为什么要使用弧度制”这一问题．在阅读文献信息之前,可以直接通过文献列表中的期刊信息做一个初步的筛选,仅阅读数学教育类比较优秀的期刊即可,如《数学教育学报》《数学通报》《中学数学月刊》等,这可以大幅度缩减数据收集的时间,也从来源上保证了文献的质量．

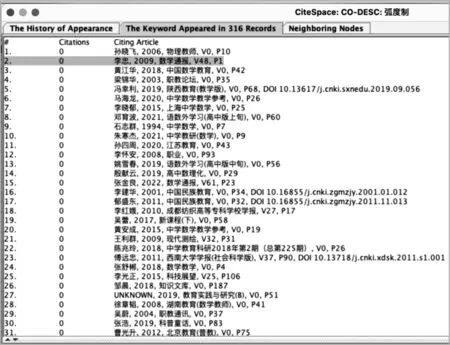
图2 含“弧度制”的文献列表

通过对上述文献列表的快速梳理,可以发现有8篇文献与“为何引入弧度制”直接相关(表1)．

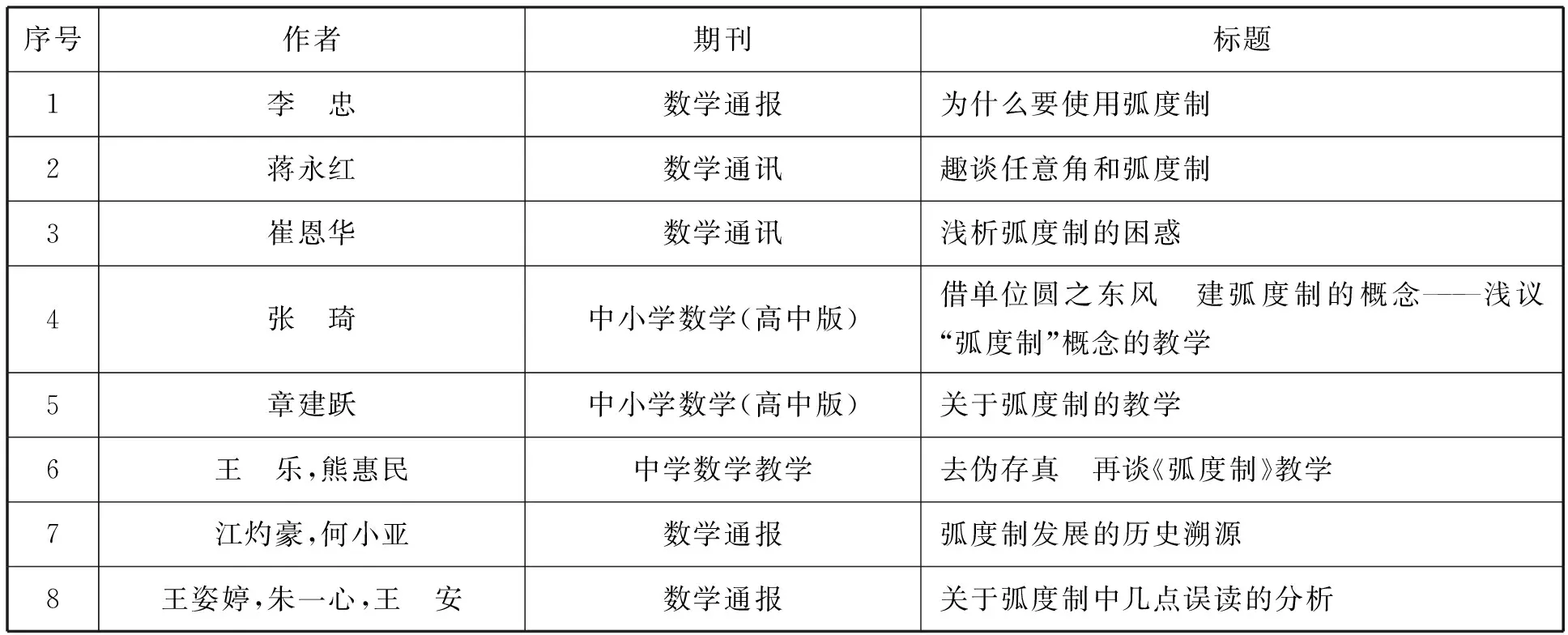
表1 与“为何引入弧度制”相关的文献

通过梳理以上文献,发现对于为什么要使用弧度制主要有四类观点:一是角度制由于是60进制,三角函数值是10进制,而函数间的定义是实数到实数间的映射,故角度制不能很好地定义三角函数;二是x+sinx这样的表达式无法运算;三是用角度制无法更为一般地描述周期性现象;四是弧度制引入的根本原因是简化微积分创立后微分、积分、泰勒展开等公式．当然,也有学者指出上述观点存在一定的错误,特别是关于角度制是否能构成实数集到实数集的映射和x+sinx无法运算的问题．综上所述,关于为何引入弧度制,学者们各陈一词,难以形成统一的观点.虽然上述观点可以让学生理解引入弧度制的必要性,但如果深究,其结论似乎不那么可靠．只有“弧度制引入的根本原因是简化微积分创立后微分、积分、泰勒展开等公式”这一观点得到学者们的广泛认同,然而在高中阶段,学生并未接触微积分内容．因此,对于弧度制的教学,教师需要深入思考,设计好基于学生知识水平的“引入弧度制的必要性”的情境问题．

3.4 “弧度制”教学理念及教学案例的探索性分析

由图1可知,“弧度制”应用的主要教学理念有深度学习、问题驱动、数学文化、数学史、APOS理论、单元教学等,基于这些理念的教学设计并非都能适配当前促进学生核心素养的教学要求,故需要进行适当的筛选．事实上,这些文献发表于不同的时期,不同时期编辑的选稿大多符合当时国家对教育教学的基本政策,以发展学生核心素养的课程目标则是在《标准2017》中正式提出,通过CiteSpace的关键词突现(图3)功能即可确定与当前教学目标最适切的教学理念．

图3 “弧度制”关键词突现知识图谱

在图3中,右侧红色粗线条表示不同关键词的突现时间范围．可以发现,具备突现强度的教学理念有基于数学史的教学、基于数学文化的教学和基于深度学习的教学,其中满足突现时间范围在2017年以后的有基于数学文化的教学和基于深度学习的教学．其中“深度学习”突现强度更高且持续至今,说明深度学习理念在当前最符合发展学生核心素养的教学理念．根据这一结果,对“深度学习”节点进行探索(细节图略),并且通过对含“深度学习”的文献信息进行深入研读,发现有5篇高度相关的文献(表2)．

通过阅读上述文献可知,深度学习的“深”主要是指学生对知识理解要深入,从知识的本质来构建知识的联系和应用,有效促进高阶思维的发展．因此,深度学习不是一种固定模式的教学框架,而是一种追求数学本质理解的教学理念．基于这种理念,可以搭配多种教学策略,如这5篇文献中,分别从问题链、变式教学、HPM、情境-问题、基于Ubd理论的逆向单元教学设计这五种方法来构建“弧度制”的深度学习课堂．教师在备课时,应结合学生学情选择最佳的教学方法,体现弧度制的数学本质．

4 结语

《标准2017》指出,教师要努力提升教学实践能力,主要关注四点:一是提升教学设计和实施能力;二是提升教学案例的分析能力;三是提升信息技术的使用能力;四是提升数学教育研究能力[5]98-99．针对当前数学教师备课现状的不足,将CiteSpace引入备课环节,帮助教师借助信息技术的优势,快速梳理教学内容的研究现状,获得教学内容基本问题的主要观点、与教学内容最适配的教学理念以及具备创新性的教学案例.教师通过对以上内容的梳理,不仅有利于个人专业的发展,还有效提高课堂教学质量,真正落实《标准2017》提出的四点要求．此外,关于信息技术的使用,当前教师更多的是通过几何画板、GeoGebra等数学软件以及希沃白板等教学平台展示数学内容,将信息技术软件用于备课环节的还不多．故本研究的意义在于落实《标准2017》提出的“教师要努力提升教学实践能力”的要求的同时,为信息技术融入备课环节提供一种可能的途径,帮助教师准确把握教学现状,设计能够真正落实核心素养理念的数学教学．