基于真实情境 提出数学问题
刘健


摘 要:以《中位数》一课为例,围绕教学任务,设计基于贴近学生生活经验、符合学生年龄特点和认知加工特点的真实情境,进而提出问题、明晰概念、应用新知、升华认识,注重情境的多样化,帮助学生形成统计观念.
关键词:真实情境;数学问题;中位数;统计观念
《义务教育数学课程标准(2022年版)》指出注重发挥情境设计与问题提出对学生主动参与教学活动的促进作用,使学生在活动中逐步发展核心素养.注重创设真实情境,可从社会生活、科学和学生已有数学经验等方面入手,围绕教学任务,选择贴近学生生活经验、符合学生年龄特点和认知加工特点的素材[1].建构主义学习理论认为,任何知识都有其赖以生存、生长和发展的背景,要想准确理解、掌握并灵活应用某一知识,就应当把握该知识的意义所在和适用范围,仅从知识的外在表现和抽象形式很难真正理解知识的内涵,这就需要理解知识赖以产生意义的背景,也就是要在一定的情境下进行学习、理解知识[2].实际教学中,教师要重视创设真实情境,并提出能引发学生思考的数学问题,也可以引导学生提出合理问题.
1 教学过程
1.1 创设情境
问题1:杭州第19届亚运会田径男子跳远决赛,经过六轮拼搏,我国选手王嘉男以8.22米的成绩夺冠,这是继上届雅加达亚运会后再次夺冠.你知道8.22米是王嘉男本次比赛的什么成绩吗?为什么平均数不能代表他的真实实力?
师生活动:学生回答后,展示王嘉男的六次成绩,得出平均成绩不能代表他的真实实力.
设计意图:平均成绩不能决定竞技比赛的结果,让学生感受实际生活中平均数的局限性,打破学生的惯性思维.
问题2:同学们,你们是不是一直盼望长大?长大后你们希望从事什么工作呢?
师生活动:带领学生观看人才市场招聘视频,展示两则招聘广告.
招聘1
由于本公司发展需要,现诚聘优秀业务员4名,月平均工资9800元,有意者速到公司面谈.
甲公司
2023.12.1
招聘2
由于本公司发展需要,现诚聘优秀业务员4名,月平均工资8600元,有意者速到公司面谈.
乙公司
2023.12.1
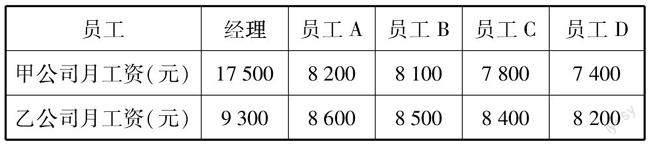
问题3:你们想去哪家公司工作呢?你们对领到的工资满意吗?为什么甲公司的员工拿到的工资远远低于承诺的工资呢?
师生活动:学生自由选择去哪家,教师分别选择四位同学作为甲乙两公司的员工模拟一个月后领工资的场景.之后,教师展示两个公司的所有员工的完整工资表,并制作统计图直观观察.
学生不难发现甲公司经理的工资远远高于其他员工的工资,所以拉高了平均工资.比平均工资高的只有经理一人,其余员工的工资都比平均工资低.
设计意图:以表格、统计图的方式呈现数据,加强知识间的联系,增强学生对数据处理和评判的意识.
问题4:你们觉得用月平均工资代表甲公司的一般水平合适吗?你们能否找到一个合适的数据代表甲公司员工工资的一般水平吗?
师生活动:学生小组讨论,教师适时引导,发现比8100元高的员工有两位,比8100元低的员工也有两位,8100元可以代表工资的一般水平.这个“处于中间位置”的工资就是今天要探究的——中位数.
设计意图:在现实情境让学生感悟中位数的必要性,从而引出本节课的课题.
1.2 变化情境
问题5:如果拿到的甲公司的工资单如下表所示,甲公司工资的中位数是多少呢?
师生活动:学生分析,教师板书中位数的定义及注意点.
设计意图:明确寻找一组数据的中位数,需要先按大小顺序排序,排序是确定中位数的前提.
问题6:现在甲公司又招聘了一名月工资是8000元的员工,甲公司工資的中位数又是多少呢?
师生活动:小组讨论后得出结论,一般地,将一组数据按大小顺序排列,如果数据的个数是奇数,那么处于中间位置的数是这组数据的中位数;如果数据的个数是偶数,那么处于中间位置的两个数的平均数叫做这组数据的中位数.
设计意图:明确一组数据的中位数只有一个,特别当数据个数为偶数时,不能把最中间两个数都作为中位数,通过计算知道中位数不一定与这组数据中的某个数据相同.
问题7:甲公司的经理的工资相对于其他员工数据偏大,拉高了平均数,那么中位数是否受其影响呢?
师生活动:教师继续增加经理的工资,平均数继续增加,但中位数不受偏大数的影响.
追问:如果一组数据中出现了偏小数据,平均数、中位数是否会受影响呢?
设计意图:明确一组数据中出现偏大或偏小数据,会拉高或拉低平均数,但中位数不受偏大或偏小数的影响.因此,当一组数据中个别数据与其他数据的大小差异很大时,通常用中位数来描述这组数据的集中趋势.
1.3 又变情境
问题8:(随机请四位身高接近的学生到讲台)
(1) 四位同学身高的一般水平用什么数表示比较合适?
(2) 增加一名班级最高学生,五位同学身高的一般水平用什么数表示比较合适?请你比较身高的平均数和中位数的大小.
(3) 请一位同学蹲下,五位同学身高的一般水平用什么数表示比较合适?请你比较身高的平均数和中位数的大小.
设计意图:通过活动情境为学生搭建交流的平台,在解决问题的过程中体验成功的乐趣.
1.4 再变情境
问题9:根据国际货币基金组织2022年4月发布的2021年世界人均GDP(美元)排名,被统计的187个国家的人均GDP的中位数为5525,中国的人均GDP为12359,请问中国处在什么水平?(GDP指在一国领土范围内,其居民无论国籍如何,只要符合本国常住居民定义,在一定时期内所生产和提供劳务价值的总和.单位:美元)
06美国69231 21英国47203 22法国44853 26日本39340
看到这组数据你有何感想?
设计意图:让学生切实感受数学在实际生活中的应用,体会数学的价值.
问题10:请谈谈本节课你的收获和体会?
设计意图:帮助学生巩固中位数的知识,深化对中位数的理解,促进学生建构新的认知结构.
2 教学思考
《中位数》属于“统计与概率”中的统计部分.统计学在社会生活中有着广泛的应用,对数据进行分析以及做出科学推断是现代公民必须具备的能力.学生在小学以及前两节课已经学习了平均数,但当一组数据的个别数据与其他数据差异很大时,平均数不能很好地描述这组数据的集中趋势,中位数便应运而生.中位数是对描述一组数据“集中趋势”的进一步完善,由此,从单一的平均数分析过渡到多元综合分析,有助于学生逐步形成统计观念.
2.1 创设情境,提出问题
创设情境,通过最近热门的世界田径锦标赛男子跳远决赛的例子,让学生在已有的认知结构上产生冲突(“平均数”行不通了),使学生积极去思考出现问题的原因,并为“中位数”概念的出场埋下伏笔.播放招聘现场的视频,创设生动有趣的情境,让学生有身临其境境的感觉,充分地激发了学生的求知欲.解决问题时組织学生畅所欲言,互相评价并完善,在自主探索中自然而然引出“中位数”这一新的概念.通过合作学习,提升学生的整体认识水平.教师以参与者身份主动加入学生的讨论,对学生的认识起促进和调节的作用.
2.2 变化情境,明晰概念
在上一招聘情境的基础上通过巧妙的变化,围绕以下教学路线展开:① 确定一组数据的中位数须先排序;② 如果一组数据的个数是奇数,那么处于中间位置的数是这组数据的中位数;如果数据的个数是偶数,那么处于中间位置的两个数的平均数是这组数据的中位数;③ 当一组数据出现偏大数或者偏小数,平均数和中位数是否受影响.数学教学是数学思维活动过程的教学,本环节教学情境的创设始终围绕中位数的概念,充分让学生感受中位数概念的形成过程,使学生在此过程中发展思维.在问题的引领下,学生逐步明确寻找一组数据的中位数的注意点,进而建构起“中位数”的数学概念.
2.3 又变情境,应用新知
通过活动情境,将抽象的数学知识以学生喜欢的活动形式出现,集知识性与趣味性于一体,既可以激发学生的思维活动,又可以活跃课堂氛围,使学生的思维活动、情绪与教学进程交融在一起,提高教学效果.接着,设置了一个开放性问题,置学生于主人翁地位,让学生利用所学知识通过数据分析,作出科学决策,在应用数学中学会创新.
2.4 再变情境,升华认识
通过与现实生活相关的真实数学情境,引导学生用数学的眼光来分析,并用数学语言给出解释,这符合培养学生“三会”的要求.因为选用的是国家统计局和世界货币基金组织最新的统计报告,其真实性和可靠性必将使学生产生积极的学习兴趣.《义务教育课程标准(2022年版)》指出要注重情境素材的育人功能.通过城镇与农村居民人均可支配收入中位数的对比,感受城乡的差距,培养学生的主人翁意识.通过对比发达国家的GDP,充分发挥数学的育人功能,培养学生的责任心和使命感,鼓励学生为了实现中华民族伟大复兴的中国梦而努力学习.
总之,中位数的教学注重情境的多样化,让学生感受数学在现实世界的广泛应用,体会数学的价值.本节课让学生经历数学观察、数学思考、数学表达、概括归纳、迁移运用等学习过程,体会数学是认识、理解、表达真实世界的工具、方法和语言,增强认识真实世界、解决真实问题的能力,树立学好数学的自信心,养成良好的学习习惯.
参考文献:
[1] 中华人民共和国教育部.义务教育数学课程标准(2022年版)[M].北京:北京师范大学出版社,2022.
[2] 涂荣豹.新编数学教学论[M].上海:华东师范大学出版社,2006.
[3] 周晓丰.指向素养达成的数学作业设计思考[J].数学之友,2022,36(1):4043.
[4] 王思俭.基于单元教学情景的新概念课堂教学设计与研究——以《导数在研究函数中的应用》为例[J].数学之友,2022,36(2):1418.
[5] 葛雯琳.厘清“明线”与“暗线”,优化问题链教学——以《正切函数的性质与图象》为例[J].数学之友,2022,36(2):3941.
[6] 李宏大.中学生几何推理能力的培养研究[J].数学之友,2022,36(3):24.

