中位数计算公式及数学性质的新认识

何文胜，陈 武，陈 尘

（1.西南石油大学 经济管理学院，成都 610500；2.中石油西南油气田分公司勘探开发研究院，成都 610056）

0 引言

在《统计学》教学中，在讲授到平均指标的时候，数值平均数一般有算术平均数、调和平均数、几何平均数等，位置平均数一般有众数、中位数、四分位数等，除各个平均指标反映的经济含义有差异之外，就是根据所掌握的资料不同所采用的计算方法有所差异。同时各个平均指标的数学性质也有一定的差异，本文根据中位数的含义及计算方法，与其他平均指标进行比较，在社会经济现象中，利用中位数的数学性质，重视中位数在统计研究和实践中的作用。

1 中位数的含义及计算

定义1：中位数是指在变量数列按照有序（升序或者降序）排列的时候，位于中间位置所对应的变量值。

也就是在一个变量数列中，比中位数小的变量值占一半，比中位数大的变量值占一半，中位数位于中间位置所对应的变量值，因此，可以用中位数反映现象的一般水平。

确定中位数的方法，在变量数列没有分组的情况下，通过计算中位数的位置=，n为变量值的个数，找这个位置对应的变量值，即为中位数，在n为奇数的时候，对应的是一个整数位置，找这个位置对应的变量值即为中位数；在n为偶数的时候，对应的是一个点5的小数位置，一般找点5小数位置的前后位置的变量值进行简单算术平均即为中位数。

在分组数列的情况下，确定中位数，一般通过计算累计次数来进行。

定义2：向上累计（或者较大制累计）次数，是指变量值按照升序排列，从第一组的次数依次向后面组次数进行的累加。

定义3：向下累计（或者较小制累计）次数，是指变量值按照升序排列，从最后一组的次数依次向前面组次数进行的累加。

定义4：单项式数列是指用一个变量值代表一个组所形成的变量数列。

在单项式数列的情况下，确定中位数的方法是先计算中位数的位置为总体单位数，在向上累计次数的时候，从第一组的累计次数开始与中位数的位置进行比较，累计次数第一次大于中位数的位置所对应的变量值即为中位数；在向下累计次数的时候，从最后一组的累计次数开始与中位数的位置进行比较，累计次数第一次大于中位数的位置所对应的变量值即为中位数。

定义5：组距式数列是指用变量变动的一定范围（或者区间）代表一个组所形成的变量数列。

在组距式数列的情况下，确定中的第一步是计算中位数的位置；第二步用累计次数与中位数的位置进行比较，找到中位数所在组，其方法按照单项式数列确定中位数的方法进行；第三步是利用组距式数列中位数的计算公式进行计算，确定中位数。

2 组距式数列中位数计算公式的推导

在《统计学》教科书上一般组距式数列计算中位数的公式有下限公式和上限公式。

下限公式：

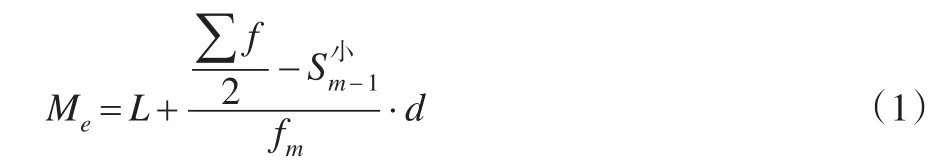
上限公式：

式中：Me为中位数；L为中位数所在组的下限；U为中位数所在组的上限为近似看成中位数所在的位置；m为中位数所在组；fm为中位数所在组的次数；d为中位数所在组的组距；为中位数所在组以前的较小制累计次数；为中位数所在组以后的较大制累计次数。

需要说明一点的就是，在几乎所有的《统计学》教科书上，对较小制累计次数和较大制累计次数都是用的相同符号表示，认为不是十分恰当，在本文中用S小和S大分别表示较小制累计次数和较大制累计次数。

组距式数列中位数计算公式的推导。

根据中位数的定义，将中位数所在组的下限、上限、较小制累计次数、较大制累计次数和中位数位置用数轴表示如图1所示。

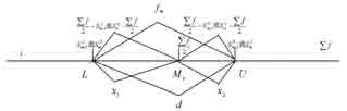
图1 组距式数列中位数位置及次数对应图

图1的说明，设L到Me的距离为x1，L到Me对应的次数为为到中位数所在组的较大制累计次数，设Me到U的距离为x2，Me到U对应的次数为为到中位数所在组的较小制累计次数，L到U的距离为d，L到U对应的次数为fm。

设组距式数列中位数在中位数组内为均匀变动，那么，距离之比与对应的次数应相等。则它们之间的比例为：

按下限公式计算：

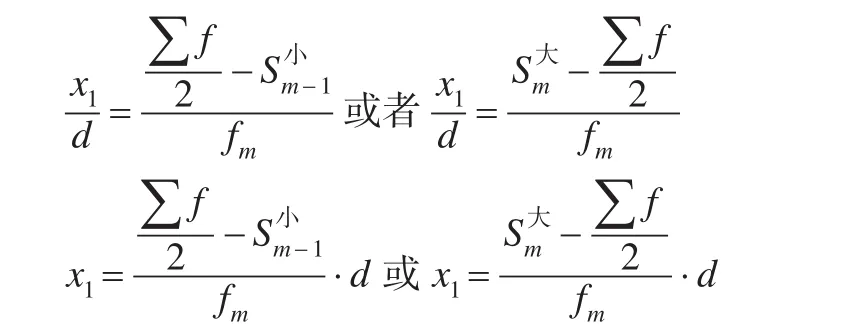
所以:

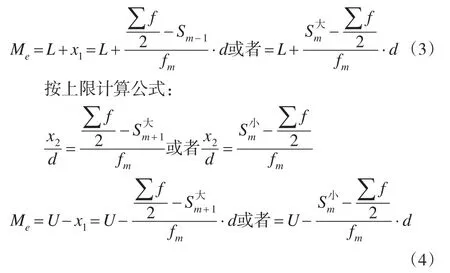
传统的《统计学》教科书上组距式数列中位数的下限计算公式通常是按照较小制累计次数进行计算的，上限计算公式通常是按照较大制累计次数进行计算的。通过推导还可以得到组距式数列中位数按下限计算的另一个公式，即是也可以按照较大制累计次数进行计算；同样还可以得到组距式数列中位数按上限计算的另一个公式，即是按照较小制累计次数进行计算，对同一资料得到的中位数计算结果是一样的。

3 中位数数学性质的新认识

在前面对变量数列中位数的计算方法进行分析后，可以对中位数的一个很重要的数学性质进行分析。

当且仅当为最小值。即是变量值与中位数离差绝对值的总和为最小。

证明过程如下：

根据中位数的定义，在数轴上表示如图2所示。

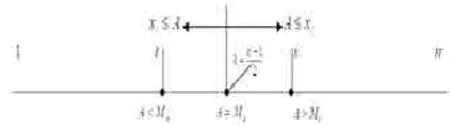
图2 中位数位置及对应变量值关系图

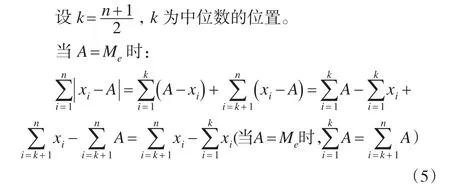
当A＞Me时：

设s点的位置对应的变量值是A，且A＞Me：

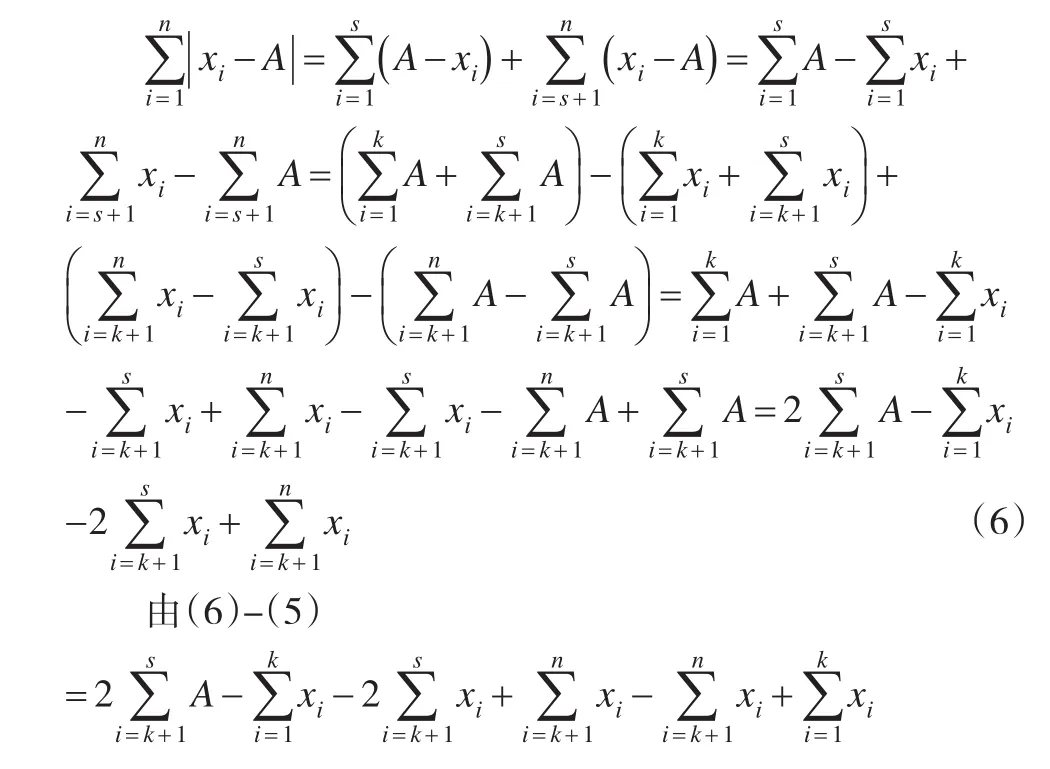
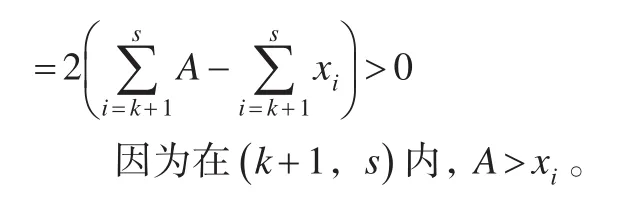
当A＜Me时：

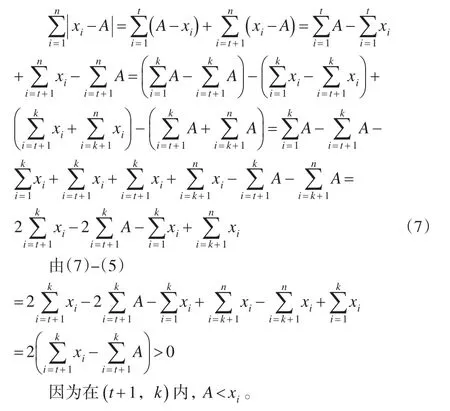
设t点的位置对应的变量值是A，且A＜Me：通过对中位数数学性质的推导，在数值平均数或者位置平均数数中，为最小值，可以看出，用中位数作为反映现象一般水平的指标更为恰当和合适。因此，在统计理论研究和统计实践中，需要重视中位数的研究和应用。

4 结论

本文通过对数值平均数位置平均数的分析，根据中位数的定义及计算方法，对中位数的计算公式和数学性质进行了推导和说明。在组距式数列中中位数的下限公式也可以按照较大制（或者向下）累计次数计算，上限计算公式也可以按照较小制（或者向上）累计次数计算，同时对传统《统计学》教科书上对组距式数列较小制（或者向上）累计次数和较大制（或者向下）累计次数所表示的符号应该加以区分；经过简单的代数变换得到，在变量数列中变量值与中位数离差的绝对值的总和为最小。因此在统计理论和统计实践中，要重视中位数的研究和运用。

参考文献：

[1] 刘竹林，江永红.统计学原理[M].合肥：中国科学技术大学出版社，2006.

[2] 施建军.统计学教程[M].南京：南京大学出版社，1992.

[3] 袁卫，庞皓，曾五一.统计学[M].北京：高等教育出版社，2000.