创设情境探究 深化思维教学
顾言

摘 要:向量是近代数学中重要和基本的概念之一,具有物理背景和几何背景.本文以人教A版必修二平面向量的概念教学为例,基于数学核心素养,通过创设情境,引导学生进行自主探究、知识迁移,以达到更高的思维教学目标.
关键词:平面向量;概念教学;自主探究;数学思维
1 问题提出
对于“平面向量的概念”这一课时,教师往往会以梳理教材中的概念为主线,着重对相关题目的反复练习,而对概念的讲解一带而过.这样的教学设计忽视了学生对概念的理解,忽视了学生实践能力的培养,忽视了学生数学思维的提升.因此,笔者在本节评优课的设计中,着重
创设探究情境,
积累学生的基本活动经验,从生活实例中抽象出平面向量,通过学生的动手操作逐步引出平面向量的相关概念并引发进一步思考,旨在培养学生动手操作的能力以及思考问题的能力,整体提升学生的数学核心素养.
2 教学实录(片段)
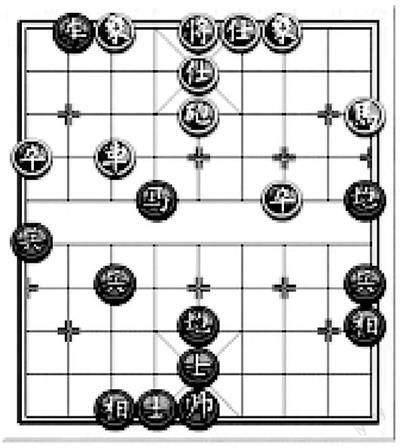
师:有没有哪位同学了解中国象棋,知道中国象棋的规则是什么?
生:象棋口诀:马走日字象飞田,车走直路炮翻山.士走斜路护将边,小卒一去不复返.
师:今天老师带来了一副棋局,下一步这些棋子可以怎么走呢?请一位同学上来演示一下.
师:这个口诀实际上描述了棋子每走一步的位移.大家能说说其他类似位移的量吗?
生:力,速度……
师:(位移、速度、力……)这些量有什么共同的特点?
生:既有大小又有方向.
师:像距离、质量、面积这样只有大小的量在物理中叫作标量,数学中叫作数量.像位移、速度、力这样既有大小又有方向的量是什么量呢?
生:矢量.
师:在物理中这样的量称为矢量,在数学中它被称为向量.
师:既有大小又有方向的量叫做向量.这就是向量的概念,今天我们来一起学习平面向量的概念.
设计意图:这里以学生比较熟悉的棋盘为背景,抽象出棋子的位移,让学生通过理解位移包含方向和大小两个元素,举例出类似的量——力和速度.教师通过归纳位移、力和速度这些量的共性引入向量的概念,即既有大小又有方向的量.
师:我们知道数量可以用实数来表示,实数可以与实数轴上的点一一对应,实际上是用几何图形也就是数轴上的一个点表示了这个实数.那么我们能不能也找到一种几何图形来表示向量?同学们可以试着表示棋盘上棋子的位移吗?
师:为什么选择用这样一个带箭头的线段表示位移呢?
生:物理中是这样表示的.
师:你知道物理中为什么要这样表示吗?
生:线段长度表示大小,箭头表示方向.
师:是的,像这样具有方向的线段叫做有向线段,它和线段一样可以表示长度,再加上箭头来表示方向.
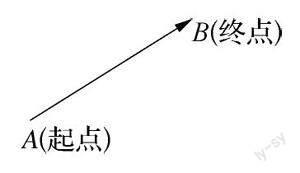
师:在线段AB的两个端点中,规定一个顺序,假设A为起点,B为终点,那么线段AB具有方向,通常在有向线段的终点处画上箭头表示它的方向.这样具有方向的线段叫做有向线段.
师:以A为起点、B为终点的有向线段记作AB,起点在左终点在右,字母上加上指向右侧的箭头.知道了有向线段的起点、方向、长度,它的终点就唯一确定了.
师:向量可以用有向线段AB来表示,我们把这个向量记作向量AB.向量也可以类似线段用小写字母a,b,c……表示,为了以示区分,这些小写字母要加粗,书写时需要在小写字母上加上向右的箭头.
师:用有向线段表示向量,可以让向量更加形象更加直观.
师:向量AB表示向量的方向是由A指向B,向量的大小如何用符号表示呢?
师:线段AB的长度是如何用符号表示的?
生:用|AB|表示.
师:类似地,我们在向量AB两侧加上相同的符号表示向量AB的大小,也就是向量AB的长度(或特殊的向量).
师:在实数轴上,哪几个实数比较特殊?
生:0,它是数轴正负的分界点.1,它到0的距离定义了数轴的单位长度.
师:我们将这种特殊性迁移到平面向量中,在向量中也有两个特殊的向量:模长为0的向量叫做零向量,记作0(书写时在必须0上加上向右的箭头).模长为1的向量叫做单位向量.
设计意图:引导学生利用迁移的思想方法,根据数量和数轴上的点的对应关系,寻找一种集方向和大小于一身的几何图形表示向量,即有向线段.有向线段的长度和方向可以分别表示向量的长度和方向.在用数学符号描述向量时,类比线段的描述方法,对线段AB加上箭头得到向量AB,用线段的长度符号|AB|也可以描述向量AB的模长|AB|.最后,引导学生将0和1在数轴上的这种特殊性迁移到向量中,定义零向量和单位向量,同时强调零向量的写法以免与数量0混淆.
師:刚才同学们在棋盘上画出的实际就是一个个向量,根据这些向量请同学们回答以下问题:
设计意图:这里根据学生在棋盘上作出的向量,定义共线向量和相等向量、相反向量,重点在于概念辨析,理解共线向量关注的是两个向量的方向,相等向量、相反向量则同时关注两个向量的方向和大小.其中,特别强调零向量对判断向量共线的干扰性以及向量平行和直线平行的联系和区别.
师:刚才这位同学提到,单位向量的模长都为1,但方向不确定,那么如果将所有单位向量的起点移到同一点O,这些向量的终点轨迹是什么呢?
思考(1):将所有单位向量起点移到同一点O,则它们终点的集合(轨迹)是什么图形?
生:以O为圆心,1为半径的圆.
思考(2):当OM与ON是相等向量时,判断终点M与N的位置关系.
生:两点重合.
师:是的,当两个向量起点相同,模长相同,方向相同时,它们的终点就被唯一确定了.
思考(3):当OM与ON是平行向量,且|OM|=2|ON|时,判断向量MN的方向与ON的方向之间的关系.
生:(学生板演)分两种情况考虑,当OM与ON方向相同时,MN与ON方向相反;当OM与ON方向相反时,MN与ON方向相同.
设计意图:思考1和思考2结合单位向量、相等向量、相反向量的定义,培养学生对于抽象的研究对象的逻辑推理能力;思考3由平行向量的方向相同或相反两种情况,培养学生分类讨论的能力.这一思考题需要整合新学的概念和定义解决问题,培养学生应对新定义的临场思考能力.
师:请同学们回忆一下本节课学习了哪些内容?向量是既有大小又有方向的量,相比数量,向量增加了方向这一重要的元素.今天这节课我们将数量和数轴上的点的对应关系迁移到向量中,用有向线段来表示向量.有向线段可以具象刻画向量的方向和大小,通过几何方法直观展现向量这一抽象的概念.在解决问题时,同学们利用几何直观想象、分析、构思,建立数学模型,对复杂的问题我们还进行了分类讨论.
师:结合本节课的内容,下面我们来做一个接龙游戏,参与有奖.
问题1:以方格纸的格点为向量的起点和终点,你能画出与给出的这个向量相等/相反/共线……的(单位)向量吗?你来画一画.画好以后请你再叫一位同学上来完成你的要求.
问题2:令小正方形的边长为1,以上这些向量的长度分别是多少?
问题3:以1×3的方格的格点为起点和终点的所有非零向量中,有多少种大小不同的模?有多少种不同的方向?
生:6种模,16种方向.
问题4:以方格纸的格点为向量的起点和终点,是否能画出任意模长的向量?
生:必须满足勾股定理,即模长的平方等于两个正整数的平方之和.
设计意图:这一部分作为开放性问题,由学生自由发挥提出和本节课内容有关的作图要求,并由同伴来完成作图,实际是对新授课内容的灵活运用,让学生积累基本活动经验,从活动中引导学生总结计数的思路和方法.最后,让学生思考是否可以提出任意模长的作图要求,从特殊到一般,培养学生学会思考并主动思考的能力.
师:向量是一门新的数学语言,是描述几何图形的基本工具,是数与形的桥梁.我们的身边有很多向量,我们的身边也处处都有数学.今天我们用数学的思想从大家非常熟悉的棋盘中抽象出平面向量的概念,接下来我们还要用向量这个工具去解决实际问题.学习语言最好的方法是用语言去表达,学习数学最好的方法就是用数学的眼光看世界,用数学的思维思考世界,用数学的语言表达世界.
3 教学反思
本节课从学生熟悉的生活情境入手,从棋盘中抽象出平面向量的概念,通过知识的类比、迁移引入平面向量的概念、表示及性质,基于学生的基本活动经验,以直观想象的核心素养贯穿始终,旨在培养学生学会观察、学会思考、学会反思的能力.
3.1 学会观察
课堂开始时笔者请学生1描述中国象棋的规则,并在课件中展示这一规则的口诀,再请学生2到黑板上演示各种棋子的走法.尽管学生2不会下象棋,但通过同学的描述以及阅读老师给出的口诀,理解并作出了正确的演示.在生活中有很多需要学习的新知识,复杂情境也是高考的大势所趋,能够对新的材料观察、阅读、理解并实践是学生未来发展的基本技能.
在引入零向量及单位向量的定义时,笔者提问数轴上有哪些特殊的实数,试图将这种特殊性迁移到向量中.在回答这个问题時,学生3能够感受到0和1这两个数字是特殊的,但在回答其特殊之处时描述的是0和1作为实数的特殊性,没有准确理解问题的本质是0和1在数轴上的作用.能够理解题意并作出对应的解答,是解决问题的基本要求.
在回答思考2当OM与ON是相等向量时判断终点M与N的位置关系时,学生4回答两点都在以O为圆心、1位半径的圆上,这一回答暴露了学生没有准确理解相等向量的定义,即向量大小相等同时方向相同,实际上两点应是重合的.对于给出的新定义,将题目条件和定义中的条件一一对应,才能准确地使用这个定义.
3.2 学会思考
在学习相等向量与共线向量的这一部分,笔者提问学生PQ,OZ,MN在大小和方向上的关系、JK,XY在大小和方向上的关系,并提问学生是否还有其他向量具有类似的关系.这里学生首先需要理解老师提出的两组向量存在的关系,再在所有的向量中筛选找出对应关系的其他向量.这需要学生具备归纳共性的能力和转化应用的能力.
对向量进行概念辨析时,需要学生思考概念和定义中的充分性和必要性,从多个角度思考问题,发现命题的漏洞.例如零向量对向量共线的干扰性,以及向量平行和直线平行的联系和区别.
在最后一个学生活动后的问题3中,学生需要对不同的模和方向进行计数.在回答模有多少种这个问题时,学生回答“1,2,5,10,2,3共6种”,笔者追问学生这样数是否有什么规律,学生回答是先固定向量的起点,再调整向量的终点以得到不同的模长,这是一种不错的思考角度,笔者引导学生也可以把向量分为沿着格边和对角线两类再进行计数.在回答第二个问题时,该生一时无法数清有多少种方向,这时候说明学生的分类方法并不适用方向的讨论,进而笔者建议用老师的分类方法试一试,学生很快就算出了结果.在这个问题中,学生需要思考如何不重复、不遗漏地计数,根据不同的情境选择合适的分类依据,先思考再行动才能高效准确地解决问题.同时,此处提到的先分类再计数是计数原理中一种重要的思想方法,在此为计数原理一节作铺垫,体现了数学中大单元整体设计的思想.
3.3 学会反思
在本节课的最后,笔者设计了一个开放性活动,笔者作出一个向量后,要求学生画出和这个向量共线的一个向量,再由学生提出新的作图要求后由另一位学生来完成作图.学生们分别提出了这样几种要求:与之模长相等的向量、与之方向相反的向量、模长为13的向量、这张方格纸内可以作出的模长最长的向量……活动结束后笔者提问学生,当以格点作为向量的起点和终点时,是否可以要求下一位同学作出任意模长的向量?这是对活动内容的反思,也是对问题本质的拷问.学生回答13是由22+32得到的,但没有在课堂上总结出一般化的结论,这样站在出题者角度进行思考的高阶思维能力需要得到不断培养和提升.
参考文献:
[1] 中华人民共和国教育部.普通高中数学课程标准(2017年版)[S].北京:人民教育出版社,2018.
[2] 喻平.数学学科核心素养要素析取的实证研究[J].数学教育学报,2016,25(6):16.
[3] 刘祖希.图说数学核心素养[J].中小学课堂教学研究,2020(10):5962.
[4] 刘祖希.图说数学单元教学[J].中学数学杂志,2022(7):1317.
[5] 章建跃.核心素养立意的高中数学课程教材教法研究[M].上海:华东师范大学出版社,2021.
[6] 罗玲连.情境认知理论对中学数学教学的启示[J].数学之友:2023,37(14):25.
[7] 刘子侨.中学数学教学问题情境创设实验研究[D].辽宁师范大学,2022.
[8] 张瑞杰.生活情境在中学数学教学中的应用[J].数学大世界(上旬),2020(6):85.

