初中数学图形解题技巧的教学思考

李建伟

摘 要：数学学科中，几何问题是常见题型中的一种，《义务教育数学课程标准（2022年版）》将“图形与几何”作为单独板块呈现，而在教学过程中，如何培养数学图形解题技巧成为难题.本文对初中数学图形解题技巧的教学进行了分析，首先对数形结合进行了概述，随后对初中数学图形解题技巧和思路进行了分析，最后对提高初中图形解题技巧教学质量的保障措施进行了探讨.

关键词：初中数学；图形；解题技巧；数形结合

数学本身是一门研究数量关系和空间形式的自然科学，其中包含“数”和“形”两方面内容.在一定条件下，“数”和“形”可以相互转化，从而从另一个角度为研究者提供思路，解开原本无法解开的问题.因此，在初中数学课程中，图形与几何占比较大，学生可以通过对图形的学习了解“数”和“形”之间的关系，利用图形具体性、可视性的特点，激发学生学习活力，解决困难，避免学生在枯燥、繁琐、抽象的计算中失去耐心，从而丧失对数学的兴趣.

1 关于数形结合的概述

1.1 数形结合的本质

数形结合本身就是对“数”和“形”进行结合.“数”指代数，是对数量关系进行研究.而“形”是指几何，主要是对空间形式进行研究.二者虽然相对独立，但是不能完全分割，反而应该相互利用，做到數形结合，让“数”和“形”相辅相成，共同成就.对于数形结合，最简单的例子就是坐标系的应用.举例而言，在研究比例时，教师可以举单价、数量、总价的例子，假设单价为X，数量为Y，总价为Z，采用坐标系教学，当X固定时，在坐标系中Y和Z呈直线上升趋势，可以得知单价固定时，数量与总价呈正比.同理，当Z固定时，坐标系中X和Y呈下降趋势，表示X和Y呈反比，可以得知总价固定时，单价和数量呈反比，由此将坐标系作为引入，让学生从图形中得到单价、数量、总价之间的关系，从而达到数形结合的目的［1］.

1.2 数形结合的使用原则

数形结合的使用原则主要包含三种：第一，等价性原则.等价性原则是指在使用数形结合的过程中，几何性质与代数性质应该是等价的.如果无法保持二者的等价性原则，会使解题过程出现漏洞，导致无法得到答案或答案不准确.同时，虽然图形较为直观，但由于图形具备一定局限性，无法对代数进行完整表现.因此，教师需要培养学生的数学能力和数学素质，从而让学生学会对数式和图形进行转换，并确保信息等价转换.第二，简单性原则.数形结合是一种解题方式但不是唯一方式，在解题过程中，学生需要对具体例题进行分析，选取合理、方便、快捷的解题方式，而非必须用代数方法解决几何问题、用几何方法解决代数问题，寻找便捷、简单的解题方式才是最好的.第三，双向性原则.由于几何与代数二者相辅相成，密不可分，当前学校中的学生多数能够利用几何方法解决代数问题，或用代数方法解决几何问题，但是在实际解题过程中，并非所有题目都能够让学生采用单一的解题方式进行解决.有时需要学生进行双向分析，同时应用代数方法和几何方法，才能体会灵活应用的感觉，发挥“数”和“形”的双向性原则［2］.

2 初中数学图形解题技巧和思路

图形解题技巧需要学生将数字和图形巧妙结合，通过代数验证几何或者通过几何验证代数，从而达到解题目的.下面以点、线段、角、平行线、相交线和三角形为例，进行数形结合解题思路应用分析.

2.1 点、线段、角、平行线、相交线相关题型

点、线段、角、平行线、相交线相关题型是几何教学中的重要内容，同时也是几何教学的起点.无论是点、线段、角、平行线还是相交线，都有其内在规律，教师针对几何进行教学就是将规律一步步推导，通过列举法或其他方法证明答案，让学生了解几何中的内在联系［3］.而应用数形结合后，教师可以将几何内容和代数内容相结合，用几何方式解决代数问题.

例如，在交点教学中，教师可以首先提问“如果有三个车站A、B、C按照顺序在一条线路上，该线路不可逆行，有几种购票方式？”引导学生进入教学情境，随后列举AB、AC、BC三种购票方式得到答案.此时，教师可以将思路转换，提问“在平面内，三条直线相交时最多有几个交点？”，通过画图的方式让学生了解最多有三个交点.

随后，教师可以继续提问四条“直线相交会有多少个交点”，依然通过画图的方式让学生了解四条直线相交最多有六个交点.

在简单列举后，教师可以对直线数量和交点数进行深入分析，经过推导得出，假设有n条直线，那么交点个数最多为n（n-1）2个.此时，由于交点的数量和线的数量之间的关系已经明确，教师可以引导学生再次回到购票问题当中，假设有5个车站，那么购票方式有5×（5-1）2（种）.从几何和代数两个方面进行深入研究，让学生领会数形结合的解题技巧，达到教学的目的.

2.2 三角形相关题型

三角形相关题型是几何教学中的重点，历年考题必出类型之一.三角形教学中的重点包含全等三角形、等腰三角形、直角三角形、相似三角形等等.以全等三角形为例，判定两个三角形全等的方法有四种，即边角边、角边角、角角边、边边边［4］.其

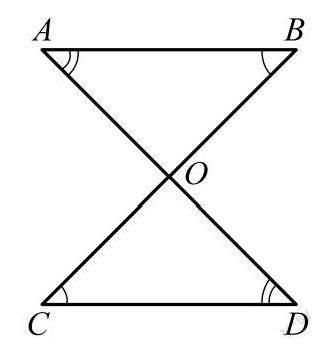
中，无论哪一种方法，都需要有一条边相等才能判定.三角形全等判定同样可以通过数形结合的方式进行讲解，比如以角边角的证明方式为例，简单画图，设AB=CD，且AB∥CD，如图所示.

由于AB∥CD，则∠BAO=∠CDO且∠ABO=∠DCO，又由于AB=CD，满足角边角分别对应相等，则可以判定△ABO≌△DCO.转换为代数则可以在图中加入数据，假设∠AOB是直角且AO=BO，则可以判定△ABO为等腰直角三角形，由于AB=CD，则△CDO也同样为等腰直角三角形，设CD为2，则AB同样为2，CO=DO=AO=BO=1，可证△ABO≌△CDO.因此，熟练应用数形结合，能够提高做题效率，同时对已有答案进行验证，确保不会出现差错.

3 提高初中图形解题技巧教学质量的保障措施

3.1 通过故事引入，深入教学内容

学生学习过程中，兴趣爱好是最好的导师.一个好的课堂，能够吸引学生的学习兴趣，让学生深入课堂之中，跟随教师详细分析知识点、解题方法.而如何激发学生的学习兴趣，是当前教师教学中的重要内容之一.情境教学法可以让学生深入情境当中，在情境里深入探索知识点.在数学课堂中，教师可以为学生设立情境、创设故事，吸引学生的注意力［5］.比如创设一个修剪花园的故事，教师为学生讲述：国王要求花匠对花园进行整理，花园形状必须是圆形，且需要花园内部规划出一片三角形区域作为小广场，其中三角形小广场的边缘需要修建一个观景台，入口处需要有一条直达观景台的小路，要求学生画出图形.如图所示，学生会画出类似图中的图形或者其他图形，教师可以根据图形设定数值，让学生根据数值求答案，或根据现有条件求证.就图而言，教师可以告知学生△ABC为正三角形，且D为BC中点，要求学生简单求证△ABD≌△ACD.或者，国王将公主关在了D点，并且即将处死，学生必须从A处进入，在最短的时间里找到公主，此时教师给出对应数据，比如圆的半径、AD⊥BC、△ABC为正三角形及其边长等条件，要求学生根据现有条件求得AD的长度，做出题目，从而达到教学的目的.

3.2 采用科技手段，增加课堂趣味

随着当前社会飞速发展，高科技手段日新月异、层出不穷，教师可以利用的工具越来越多，为教师教学提供了充足的便利条件.在过去，学校教室中只有黑板、粉笔、黑板擦等简陋工具，数学教师通常会携带三角板、圆规等教学道具，偶尔会有显示屏作为教学设备供教师使用.如今，电脑投屏、投影仪、电脑、电视等设备走进千万家学校，为教师提供了充足且便利的条件，让教师发挥自身特长.教师需要采取科技手段，方便自身教学的同时激发学生学习兴趣，增加课堂趣味［6］.

比如，在进行正、反比例坐标教学时，教师可以利用电脑、投屏投影仪等设备，为同学绘制图象，吸引学生注意力的同时用不同颜色的画笔进行标注，使图形更加清晰明了，方便学生查看，使学生分辨条件时更加轻松.或者在进行勾股定理教学时，教师可以用科技手段构筑直角三角形.原有条件下，教师只能通过改数字的方式让学生了解边长3、4、5和边长6、8、10的三角形具备相似性，无法通过直观感受让学生深入体会勾股三角形.如今，教师可以利用科技手段，首先构筑一个边长分别为3、4、5的直角三角形，对学生进行勾股定理教学，让学生了解勾股定理的本质.随后对原有三角形进行缩小或放大，将长度为3的边扩大到6，学生会直接感受整个三角形都进行放大，从而深入体会勾股三角形的相似性.

3.3 展开小组讨论，鼓励学生参与

小组讨论是当前课堂中常用教学方式之一.学生的学习兴趣本身分为直接兴趣和间接兴趣，直接兴趣就是学生对学习本身具备兴趣，愿意将精力投入到学习当中.而间接兴趣即导向性兴趣，就是学生完成学习时能够收获部分奖励，将奖励作为目标进行学习.初中生本身处于爱玩、爱交友的年龄段，展开小组讨论能够培养学生的间接兴趣，将同学之间在交流、团队协作后的收获、成功后的成就感作为间接兴趣的目标，鼓励学生积极参与，最终达到教学的目的.

比如，在进行平行线判定的教学时，教师可以首先提出问题“如何证明两条直线平行”，为学生明确学习目标.其次，教师可以通过画图的方式，以直角为例，教会学生证明平行四边形的方法.如图所示，通过BD⊥AB和BD⊥CD，证明AB∥CD，让学生对平行线的判定方式有初步了解.

随后，教师划分小组，并对学生提出疑问“既然直角可以，锐角是否可以？”，引导学生进行思考，展开小组讨论，由小组成员绘制图形，深入探索平行线的判定条件.如图所示：

最后，教师要求学生对探索内容进行总结，归纳出证明平行线的条件，教师就探讨结果的正确性进行分析，引导学生一步一步了解平行线的性质，达到教学的目的.同时，教师需要对学生在小组教学中的表现进行评价，让学生收获成就感并进行反思，达到全方位教学的目的.

3.4 反复进行练习，牢记知识内容

大量的练习能够让学生将知识点融会贯通，并加以利用.数学学科与其他学科不同，数学学科只需要按照既定步骤、流程，并沿用公式、性质即可求解，得到正确答案.因此，学生解题只需要满足三个条件，第一，看懂题目.读题是数学学科的必备内容之一，数学题目通常会在题干中设下陷阱，让学生防不胜防.由于在题干中设置陷阱会决定计算方向，误解题目要求就会导致计算过程远离题目，最终得到错误答案.因此，教师首先需要带领学生进行读题方面的练习，让学生在学习、做题的过程中养成谨慎的性格.第二，熟记公式和定理.对于平面几何而言，公式和定理是数学中的真理，无论是代数还是几何解题，都离不开公式的应用.运用公式可以节省解题步骤和时间.比如在直角三角形中，30°角所对的直角边是斜边的一半，此定理能够为学生节省大量解题时间.如果学生不知道该定理，依然可以通过直角三角形的特性进行计算，最终得到短边∶长边∶斜边的比例是1∶3∶2，求出斜边或短边长度，从而进行下一步计算.第三，灵活运用公式.单纯记忆公式无法解题，学生还需要在解题中对公式和定理进行灵活应用，一方面可以节省解题时间，另一方面可以开拓解题思路.会背和会用一直是两个概念，二者相辅相成，密不可分，学生只有同时做到才能快速解题.因此，教师需要针对内容对学生进行大量训练，通过反复刷题、练习的方式让学生熟练掌握解题技巧，牢记知识内容，从而培养灵活的思维和大脑活跃度，实现全方面发展.

4 结束语

能否使用数形结合解决问题是反映学生数学素养高低的重要表现之一，如果学生仅能够在几何中应用代数，或在代数中应用几何，则学生的数学素养依然需要提高.教师首先需要让学生了解数形结合的使用原则，并将其融入日常解题当中，其次对学生进行线段、角、平行线、相交线、三角形、平行四边形、圆等形状教学，让学生了解图形的特性，最后通过故事引入、科技手段、小组讨论、重复练习等方式提升教学质量，让學生在学习中体会变通思维，培养数形结合的解题习惯，最终才能让学生收获初中数学的专业性知识，达到教育的目的.

参考文献：

［1］ 薛月.初中数学图形解题技巧的教学思考［J］.启迪与智慧：下，2020（8）：93.

［2］ 马亚喃.初中数学几何解题技巧探究［J］.数理天地：初中版，2022（18）：1718.

［3］ 孙明松.初中数学圆的解题技巧研究［J］.数理天地：初中版，2022（5）：8485.

［4］ 陈小春.初中数学数形结合题型的解题技巧［J］.数理化解题研究（初中版），2014（11）：17.

［5］ 黄华强.初中数学解题技巧指导与运用分析［J］.名师在线，2021（21）：5152.

［6］ 熊宁.巧用数形结合，提高初中数学解题效率［J］.读与写：上旬，2019（6）：1.