回归基础寻思路 提炼模型促思维

刘芝齐

摘 要：初中数学教学过程中，解题教学是非常重要的內容.解题的作用是对所学的基础知识进行巩固，通过解题的过程来提升学生的解题技巧和技能，从而培养学生的解题能力.本文将以2022年成都市中考数学26题为例，分析如何在解题过程中通过基础知识来寻找解题思路，从而通过解题来构建出相似问题的解题模型，促进学生数学思维的培养.

关键词：初中数学；解题教学；模型提炼；数学思维

从数学解题教学的过程中可以发现，所有的数学问题都是从一个较为基础的知识点出发，通过数学模型的构建而形成的［1］.所以在解题教学的过程中就需要对数学问题的基础知识进行分析，通过基础知识来寻找解题的思路，从思路中找到这类问题的数学模型，从而实现对数学思维的培养［2］.笔者将结合自身多年的数学教学经验，来对试题的解答进行探究.

1 原题呈现

例1 （2022年成都市中考数学第26题）如图1所示，在矩形ABCD中，AD=nAB（n＞1），点E是AD边上一动点（点E不与A、D重合），连接BE，以BE为边在直线BE的右侧作矩形，使矩形EBFG∽矩形ABCD，EG交直线CD于点H.

（1） 【尝试初探】在点E运动的过程中△ABE与△DEH始终保持相似关系，请说明理由；

（2） 【深入探究】若n=2，随着E点位置的变化，H点的位置随之发生变化，当H是线段CD的中点时，求tan∠ABE的值；

（3） 【拓展延伸】连接BH、HF，当△BFH是以FH为腰的等腰三角形时，求tan∠ABE的值（用含n的代数式表示）.

2 试题分析

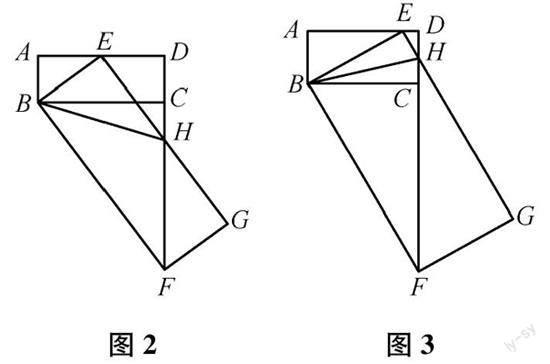
首先是第一个问题，证明两个三角形相似的方式有很多［3］，结合本题可以发现，△ABE与△DEH都是直角三角形，同时∠AEB+∠DEH=90°这个关系是恒定不变的，所以根据这两个三角形两角对应相等即可证明△ABE∽△DEH.然后是第二个问题.通过对已知条件进行分析，要求tan∠ABE的值就需要求线段AE与线段AB之间的比值关系.所以就需要根据题目中所给定的线段关系来对线段的长度进行假设，假设DH=x，AE=y，则有AB=2x，AD=4x，DE=4x-y，然后根据第一问中所证明的△ABE∽△DEH就能够对x，y的值进行计算，最后就可以计算出tan∠ABE的值.最后是第三个问题，根据题意连接BH、HF，△BFH是以FH为腰的等腰三角形，这里需要分为FH=BH和FH=FB两种情况进行讨论，当FH=BH时，如图2所示.可以很容易地证明△BEH≌FGH，从而就可以得到EH=GH，然后根据△ABE∽△DEH就能够对tan∠ABE进行表示了.当FH=FB时，如图3所示.这里就需要证明△ABE∽△CBF，从而通过证明△BEH≌△BCH来得到BE=BC，从而表示tan∠ABE的两条直角边.

3 解题过程

解：（1） 在Rt△BAE中，∠ABE+∠AEB=90°.

又因矩形ABCD与矩形EBFG相似，

所以∠BEG=90°，

所以∠AEB+∠DEH=90°，

所以∠ABE=∠DEH.

又∠BAE=∠EDH=90°，

所以△BAE∽△EDH.

4 试题总结

通过对这个试题的分析和求解可以看出，本题最基础的内容就是三角形的相似问题.在第一个问题【尝试初探】中通过证明两个三角形的相似来为我们提供了一个模型：在一个矩形ABCD中，AD=nAB（n＞1），点E是AD边上一动点（点E不与A、D重合），连接BE，以BE为边在直线BE的右侧作矩形，使矩形EBFG∽矩形ABCD，EG交直线CD于点H.在这个模型中会出现一个恒定的三角形相似关系就是△BAE∽△EDH.通过这个三角形的相似关系，就可以结合两个三角形相似情况下存在的边的关系和角的关系来解决后续问题［4］.在第二问【深入探究】中，则给了一个特殊的情况，边长关系为AD=nAB，n=2，同时点H是CD边的中点.在这个数学模型中存在这样的一个特殊关系时，就可以把两个相似三角形的边通过比值关系来进行表示，从而就可以计算出tan∠ABE的值.而在第三个问题【拓展延伸】中，则是进一步在这个相似矩形的模型中讨论，在形成等腰三角形的基础上，如何表示tan∠ABE的值［5］.

所以在这个压轴题中，试题最基础的逻辑就是在这个相似矩形的模型中会的关系△BAE∽△EDH，然后在这个相似三角形关系的基础上来进行一定的变化，从而来进行延伸.所以在解题的过程中找到题目中最基础的知识点是非常重要的，通过这个知识点来结合相应的数学模型就能够对试题进行分析和求解.当然在这个问题中，我们还能够进行更加深入的延伸.在第三问的情况下是否会存在△BFH是等边三角形的情况，如果存在，请计算tan∠ABE的值，如果不存在，请说明理由.在这个问题的讨论中就可以先假设这个结论存在，那么就能够得到的关系是BF=BH=FH，这样就可以得到BH=EG，显然这样的关系是不存在的.

5 结语

综上所述，文章通过2022年成都市中考数学压轴题26题的分析和求解过程来对试题中所考查的基础内容进行了分析，并对这个基础内容的模型类型进行了分析，由此可见，一个数学问题是通过一个或者多个基础知识并结合相应的数学模型进行不断变化而形成的.所以在解题教学的过程中就需要让学生进行基础知识的分析，结合相应的模型情况来实现对问题的求解.

参考文献：

［1］ 陈维强.初中数学教学中培养学生解题能力的策略初探［J］.课堂内外·初中教研，2022（1）：3839.

［2］ 郑旭林.夯实数学基础提高解题能力--对提高初中数学解题能力的几点分析和建议［C］.//广东省初等数学学会第二届第一次学术会议论文集.2018：120126.

［3］ 李雷.初中数学规律探究问题的类型及解题技巧探究［J］.考试周刊，2021（22）：7172.

［4］ 向勇民.初中数学教学中如何培养学生的解题能力［J］.中外交流，2021，28（3）：594.

［5］ 马亚喃.初中数学几何解题技巧探究［J］.数理天地（初中版），2022（18）：1718.