指向核心素养发展的高中数学结构化教学设计

高碧怡 张然然

【摘要】数学结构化教学旨在将零散的知识点进行模块化整合，帮助学生梳理数学知识结构，架构起良好的认知框架，形成结构化的学习方式，进而促进学生数学核心素养的发展.文章以“幂函数”为例展开结构化分析，从知识的萌芽点、新旧知识联系、新知探究、巩固练习和归纳概括五个环节，以及知识结构、认知结构、思想方法结构和教学过程结构四个维度展开讨论，探索能够促进学生数学核心素养发展的结构化教学设计基本框架.

【关键词】数学核心素养；结构化教学；幂函数

【基金项目】广东省教育科学规划课题“指向师范生教学能力发展的数学结构化教学策略构建”（项目编号2021GXJK380）；广东省本科高校教学质量与教学改革工程建设项目教学团队项目“数学教育课程教学团队”.

《普通高中数学课程标准（2017年版2020年修订）》明确提出“优化课程结构”要求.由于教材编写的特点、教学课时的分散性以及固化思维的影响，不少高中课堂呈现出碎片化的特点，不利于学生对数学知识的整体认知和数学核心素养的发展.而结构化教学的核心是培养和发展学生的自主建构能力，以发展思维为导向，以数学学科知识为载体，最终落实培养学生数学核心素养的目标.

一、数学学科结构体系简介

数学具有其自身的结构体系，包括知识结构、认知结构、思想方法结构和数学知识教学的过程结构.其中，知识结构是数学知识按照其内容各要素之间的逻辑关系组织起来的整体结构.认知结构是学生在数学学习过程中系统性地整合数学知识结构，并反映在头脑中所形成的观念体系.思想方法结构是指以数学思想为核心，所包含的相互联系、转化与渗透的结构体系，它是数学结构中的内隐性结构.同类的数学知识有着相类似的教学过程，通过结构化的教学过程可以引导学生掌握一类知识的自主学习途径，将客观存在的数学知识结构内化为头脑中的认知结构.

二、“幂函数”结构化教学设计及分析

（一）教材分析

本节选自普通高中教科书数学必修第一册人教A版第三章第三节，教材通过实际背景抽象出幂函数的概念并借助5个特殊幂函数图像，运用数形结合的方式研究幂函数的性质，总结出研究一类函数的基本路径，即背景—概念—图像—性质—应用.本节课蕴含由特殊到一般、数形结合、归纳的数学思想方法，凸显数学抽象、逻辑推理、直观想象和数学运算的数学核心素养.

（二）教学目标

1.通过对5个函数解析式的观察分析，感受幂函数概念的抽象过程，了解幂函数的概念，会表示幂函数，能够准确地描述幂函数的特征.

3.在建构幂函数的概念和探究其图像和性质的过程中，体会由特殊到一般、归纳、数形结合等数学思想方法，发展数学抽象、直观想象、逻辑推理和数学运算等数学核心素养.

（三）教学重难点

重点：了解幂函数的概念；分析归纳出幂函数的性质，掌握研究函数的一般路径.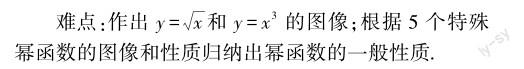

（四）教学过程

1.重视数学知识结构，抓住知识的萌芽点

以研究函数的一般路径以及幂的意义为出发点，构建起探究幂函数的脚手架，借助结构图串联零散的知识点.

【问题一】请同学们尝试梳理出函数知识点的框架结构图.

教师引导：可以从“是什么？”———函数是什么？“怎么样？”———函数怎么表示、有什么性质这些角度进行梳理.

师生活动：教师引导学生运用知识框架图回顾旧知，共同得出图1.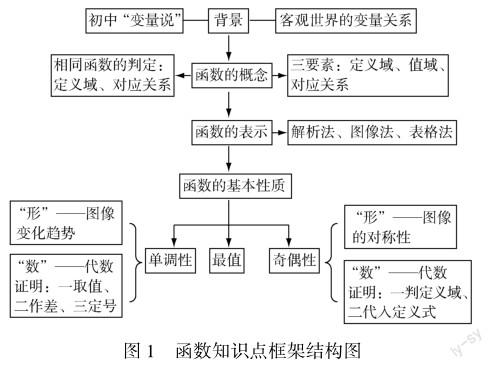

【问题二】在初中初步探究一次函数、反比例函数和二次函数时，采取了怎样的研究路径？

【问题三】本节课认识一类新的函数———幂函数，何为幂函数？同学们你们还记得什么叫作“幂”吗？

评析 设计复习环节，引导学生梳理与本节课相关的数学知识结构，抓住知识的萌芽点，从旧知出发建构新知，培养学生运用知识框架图串联零碎知识点的习惯，培养学生的结构意识，让学生在复习过程中感受数学知识的系统性.

2.结合實例抽象概念，以旧知构建新知

由于学生抽象思维的发展尚未完善，对于抽象的幂函数的概念存在一定的困难，教师可以借助实例归纳共性，以旧知为基础构建新知，降低学生的理解难度，激发学生对新知的求知欲.

【问题一】完成以下填空，并判断等式中是否存在函数关系.

【问题二】将上述5个函数解析式中的自变量和因变量分别用x和y表示，观察5个式子之间有哪些共同的特征？自变量所在的位置有何特点？

归纳共同特征：

（1）都具有幂的形式；

（2）以幂的底数为自变量，幂的指数都是常数，都形如y=xα的形式.

幂函数概念：函数y=xα叫作幂函数，其中x是自变量，α为常数.

【概念辨析】判断下列函数是否为幂函数.

（1）y=x4； （2）y=2x2； （3）y=2x；

（4）y=x-2；（5）y=x3+2.

评析 经历抽象幂函数概念的过程，从学生对“幂”的原有认知出发构建起幂函数的概念，感受数学知识之间的内在联系，体会由特殊到一般抽象函数概念的数学思想方法，初步感受数学知识内隐的数学思想方法结构体系，发展数学抽象和逻辑推理数学核心素养.

3.借助信息技术深入探究性质，以“形”助“数”凸显教学过程结构

探究幂函数的性质是本节课的难点，教师可以通过对直观图形的动态演示，引导学生更深入地剖析幂函数的性质.

【问题一】运用什么路径研究幂函数？研究幂函数的哪些方面？

师生活动：回顾初中研究函数的一般路径，得出图2.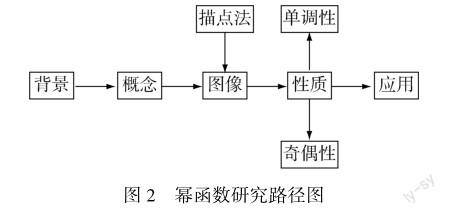

【探究一】在不同直角坐标系中分别作出前面5个幂函数的图像，结合函数解析式与图像观察并归纳幂函数的性质.

教师引导：作图时要注意什么？能否借助前两节学习的内容简化作图步骤？

评析 借助路径图（图2）回顾研究函数的一般路径，激活学生对函数知识的原有认知，在此基础上展开对幂函数图像和性质的探究，让学生感受探究函数的过程不是零散的，而是具有一定路径的，感受数学知识教学过程的结构性特征.

在利用函数的基本性质简化幂函数的作图过程并借助图像分析归纳幂函数的性质的过程中，学生能体会数学知识之间的内在联系，内化知识结构，构建起对函数的良好认知框架，同时渗透数形结合和归纳的数学思想方法，发展直观想象和逻辑推理核心素养.

【探究二】在同一平面直角坐标系中作出5个函数图像，观察图像，分析归纳幂函数的一般性质.

教师引导：（1）在（0，1）内取更多的点作出函数图像，注意公共区域内图像相对位置的高低，观察不同函数在公共区域内的增长速率.

（2）遵循从整体到局部的原则，从整体上，观察函数图像在整个直角坐标系上的分布特点；从局部上，观察5个函数图像在特定象限的分布特点，探究共性思路图（如图3）.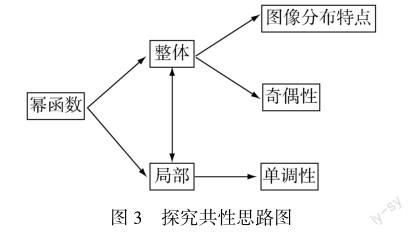

【问题二】从函数图像在各象限的分布特点来看，它们有哪些共性？

预设回答：5个幂函数在第一象限都有图像分布，在第四象限都没有图像分布，图像都经过（1，1）點.

【问题三】函数的基本性质中，哪些反映函数的整体性质？哪些反映局部性质？

【追问一】从函数的奇偶性看，存在哪些共性？从函数的单调性看，存在哪些共性？

【追问二】幂函数在（0，+∞）上的单调性与函数解析式存在怎样的联系？

师生活动：动态演示改变常数α的值时幂函数图像的变化趋势，引导学生观察图像总结特性：当α>0时，幂函数在（0，+∞）上单调递增；当α<0时，幂函数在（0，+∞）上单调递减.

【问题四】除了上述结论，你还能从动态演示中发现哪些特点？当α>0时，随着α的增大，函数图像有什么变化？α<0呢？

评析 借助信息技术直观展示5个函数图像分布及图像随α变化的趋势，遵循从整体到局部的原则对幂函数的图像进行观察，给予学生探究幂函数共性的方向，运用知识结构框架图梳理探究幂函数性质的一般思路，为今后研究其他函数的性质提供思路，感受数学知识学习相类似的过程结构.学生按照从整体到局部的原则抓住知识之间的关联点，构建新知，架构起完整的知识结构，促进良好认知结构的形成，发展学生直观想象和逻辑推理核心素养.

4.以“数”辅“形”，强化认知结构

上述教学过程主要从“形”的角度展开对幂函数的探究，接下来教师通过例题及课后习题，引导学生从“数”的角度探究幂函数的性质，并检验学生对本节课知识的掌握程度.

评析 通过例题引导学生借助研究函数基本性质的学习经验，在从“形”的角度研究幂函数性质的基础上，过渡到从“数”的角度运用演绎证明的方式进一步探究幂函数的性质，体会运用数形结合研究一类函数性质的思想方法，发展逻辑推理和数学运算核心素养.

5.归纳概括，优化认知结构

【问题一】本节课主要学习了哪些内容？运用了哪些数学思想方法？

【问题二】研究一类新函数的一般思路是什么？

评析 以问题的形式引导学生回顾本节课的主要内容、研究思路和方法，并借助知识结构图梳理出本节课的知识框架、蕴含的数学思想方法，帮助学生搭建本节课的知识框架，掌握研究一类函数的一般路径，体会研究函数的过程结构，促使学生在头脑中形成对函数的良好认知结构，逐步形成结构化的学习方式.

结 语

“幂函数”的教学旨在帮助学生掌握探究函数的一般路径及思路，形成结构化的学习方式，发展数学核心素养.指向数学核心素养发展的结构化教学要求教师不断革新教育理念，从学生的实际学情出发，站在宏观的角度统整数学知识，善于借助信息技术突破难点，把数学核心素养培养落实到课堂教学的各个环节.

【参考文献】

[1]朱俊华，吴玉国.基于单元整体的小学数学结构化教学[J].中小学教师培训，2019（9）：60-63.

[2]中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）[M].北京：人民教育出版社，2020.

[3]洪梦，吴立宝.指向“四个理解”的幂函数教学设计研究[J].中学数学研究，2020（10）：1-5.