增强中学数学习题讲评课有效性的策略探究

刘国辉

【摘要】以充分发挥习题讲评于初中生数学学习效率提高、审辩式思维形成所起的增益作用为主要目的，文章对学科核心素养视域下增强初中数学习题讲评课教学有效性的策略展开了紧密结合典型中学数学例题的案例分析，主要包含从教师讲题到学生说题、从反思错题到剖析错因两个方面，意在通过对初中数学习题讲评方式的优化与创新，切实突出数学习题及习题讲评对初中生数学学习能力、问题解决能力与高阶思维能力发展的积极影响，助力初中生数学核心素养稳定发展.

【关键词】初中数学；习题讲评；有效性；教学策略

【基金项目】本文系甘肃省教育科学“十四五”规划课题《基于“双减”背景下实施“一题一课”初中数学习题课教学研究———以“图形与几何”复习课、讲评课研究为例》阶段性成果，立项号：GS[2022]GHB0910.

习题讲评课是初中数学课程中极为重要与关键的教学课型，在促进中学生复习巩固数学“四基”，推动学生发展形成数学“四能”与实现数学“三会”等方面发挥着不可替代的重要作用.然而，就目前的初中数学习题讲评课教学实况而言，大多数师生往往会将习题讲评的焦点过于集中在对错题、例题或某一典型习题的讲解与评析之上，使得中学数学习题课教学存有较强的“师授生受”师本化倾向，从而制约了数学习题讲评课有效性的提升.下面笔者便以克服当前中学数学习题讲评课教学弊端为锚点，对增强初中数学习题讲评课有效性的策略展开探讨.

一、从教师讲题到学生说题，在“说题”中发展学生说理能力

说理能力，是一种将事实证据与推理过程寓于语言文字组织之中，以有条理、有逻辑的语言表达方式呈现而来的能力素质.在学科核心素养视域下的初中数学习题讲评课教学中，教师可在及时更新个人教育观念及思想理念的基础上，以培养学生独立思考能力、逻辑推理能力、数学语言表达能力及自主学习能力为切入点，组织引导学生效仿教师的习题讲评方式，展开数学说题活动.在有效克服以往“灌输式”“填鸭式”等数学习题讲评方式对学生数学学习效率提升的制约的基础上，让学生通过说明习题解题规划与讲解习题解题过程，稳定提升数学解题能力，发展形成数学核心素养.

（一）“说”解题规划，温故知新，培养学生认真审题的习惯

初中生是正值青春期的青少年，在数学解题过程中常会受年龄发展特征的影响而出现“急于求成”心理，主要表现在无法“沉下心来”细致分析题意和难以“静下心来”认真解析题干两方面，这便导致学生往往会因审题不透彻、不深入而出现错题.在初中数学习题讲评课中，指导学生开展说题活动时，教师就可让学生在阅读题干后说出自己的解题规划，鼓励学生“走弯路”，以此促使学生养成良好的审题习惯，并实现对已知的主动迁移和类比推理.

以人教版七年级上册数学教材“实际问题与一元一次方程”一课中习题3.4第9题为例.

例1 某糕点厂中秋节前要制作一批盒装月饼，每盒中装2块大月饼和4块小月饼，制作1块大月饼要用0.05kg面粉，1块小月饼要用0.02kg面粉，现共有面粉4500kg，制作两种月饼应各用多少面粉，才能生产最多的盒装月饼？

解析 本题的考查点在于用一元一次方程解决实际问题.学生根据题中的等量关系式列出一元一次方程，同时综合应用“合并同类项与移项”“去括号与去分母”两种一元一次方程解法求解.对于首次接触一元一次方程的七年级学生而言，如何根据题干中的已知条件找到大、小月饼数量之间的等量关系与制作大、小月饼所需面粉克重等量关系设定未知数x和列出方程是解答本题的难点.在指导学生说出解题规划时，教师可通过营造和谐、开放、宽泛的课堂教学氛圍的方式，促使学生自由表达.由此，学生便会生成如下各不相同的解题规划：

解题规划五 用方程解题.设共制作大月饼x块，根据每盒中装2块大月饼和4块小月饼，可知小月饼数量为2x块.已知制作1块大月饼要用0.05kg面粉，制作1块小月饼要用0.02kg面粉，可得制作大、小月饼的面粉用量分别为0.05xkg，0.04xkg.现有面粉共4500kg，可得方程0.05x+0.04x=4500，合并同类项可解方程，再做乘法就可得到制作大、小月饼的块数和面粉用量.

在此之后，教师可组织学生在课堂中从方法应用得体性、解题过程简便性、问题结果准确性等多个方面，对同学提出的不同解题想法与规划进行点评.在促进学生观点碰撞，引发学生思维冲突的基础上，进一步加深学生数学审题的深刻性、全面性，使其充分感知到，在解决数学问题的过程中积极联系已知与认真仔细审题的必要性，进而实现学科知识迁移，养成良好的数学审题习惯.

（二）“说”解题过程，查缺补漏，提高学生数学解题能力

初中生在解答数学问题的过程中，所书写出的解题步骤往往能够反映出学生的真实解题思考过程与数学知识、技能技巧、思想方法的掌握程度.在学科核心素养视域下的初中数学习题讲评课中，教师可在学生将头脑中生成的解题想法与规划物化为数学解题过程后，将学生的解题步骤书写情况呈现出来，组织学生以合作探究的方式评价、分析彼此的解题过程，并指出对方与自己解题过程的闪光点和不足，在充分彰显习题讲评助学、辅学作用与价值的同时，确保学生的数学解题能力能够在查缺补漏与去粗取精的过程中得以平稳提升.

以人教版七年级下册数学教材“平行线的性质”一课中习题5.3第4题为例.

例2 如图1，a∥b，c，d是截线，∠1=80°，∠5=70°，∠2，∠3，∠4各是多少度？为什么？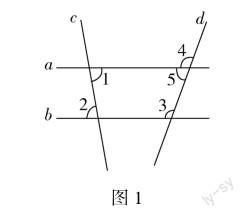

解析 本题的考查点为对平行线性质的掌握及应用.在解答本题时，初中生应严格遵循数学证明题的解题步骤与过程，将已知、定义、定理、条件、推理和基本事实呈现出来.相较于其他数学问题，本题的难度并不大，致使初中生出现错题的主要成因在于，多数学生在求解与书写解题步骤时常会忘记将对应的条件列在解题步骤之后.究其根本，是因为初中生尚未养成严谨规范的数学解题习惯.对此，教师在学生完成解题步骤的书写后，就可组织学生扮演“教师”角色展开“阅卷”活动，并说出彼此解题过程中的“失分点”与“得分点”.

解题过程一 ∵a∥b，c，d是截线，

∴∠2=∠1=80°，

∠3=∠4=180°-∠5=180°-70°=110°.

解题过程二 ∠2=80°，∠3=∠4=110°.

理由如下：∵a∥b，c，d是截线，∠1=80°，∠5=70°（已知），

∴∠2=∠1=80°（两直线平行，内错角相等），

∠3=∠4（两直线平行，同位角相等）.

∵∠4=180°-∠5=110°（互补角之和为180°），

∴∠3=∠4=110°（等量代换）.

学生在从“教师”的视角评价与分析上述两个同学的解题过程与解题步骤书写情况时，便会主动指出“解题过程一”中的不足，且能够认识到“解题过程二”的完善性，从而自觉自发地回想自己的解题过程，进行积极正向的修改与完善.在这一过程中，学生不但能够自行查缺补漏与反思内省，其数学解题能力也会随良好数学解题习惯的形成而提高.

二、从反思错题到剖析错因，在“析错”中进阶学生思维能力

错题是初中数学习题讲评课教学中不可多得的教学资源.在学科核心素养视域下的初中数学习题讲评课中，教师可一改以往的错题讲评方式，啟发引领学生从错题集的整理转向对数学错题成因的分析上.在最大化凸显错题对学生数学学习问题反馈调节作用、数学学习效率提高增益作用及数学学习习惯形成塑造作用的同时，让学生通过积极参与一系列关联性更强、综合性更突出的“析错”“改错”“避错”等数学实践活动，得到数学解题思路的开阔与思维能力的进阶.

以人教版八年级上册数学教材“三角形全等的判定”一课中习题12.2第13题为例.

例3 如图2，在△ABC中，AB=AC，点D是BC的中点，点E在AD上.找出图中的全等三角形，并证明它们全等.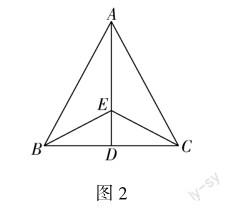

错因分析 本题的考查点为对三角形全等的判定条件与性质的灵活运用，以及数学证明题一般证明步骤的规范书写.在解答本题的过程中，八年级学生常出现的解题错误主要有三种，一为找出的全等三角形不全；二为证明题求证过程书写不规范；三为全等三角形证明条件缺失.教师在习题讲评课中，引导学生围绕本题开展“析错”活动时，可先将正确规范的解题步骤呈现出来，让学生在对比、分析与评述的过程中，由衷地意识到自身的数学错题成因，并在认识错题、改正错误与规避错误之中，持续进阶数学思维能力和数学解题能力.

正解 图中的全等三角形有三对：△ABE≌△ACE；△BED≌△CED；△ADB≌△ADC.证明过程如下：

错题一 图中的全等三角形有两对：△ABE≌△ACE；△BED≌△CED.证明同上，过程略.

错题二 图中的全等三角形有三对：△ABE≌△ACE；△BED≌△CED；△ADB≌△ADC.证明过程如下：

∴△ABE≌△ACE（SSS）.

错题三 图中的全等三角形有三对：△ABE≌△ACE；△BED≌△CED；△ADB≌△ADC.证明过程如下：

求证：△ABE≌△ACE.

证明：∵AB=AC，且AE是△ABE和△ACE的公共边，

∴△ABE≌△ACE.

求证：△BED≌△CED.

证明：∵△ABE≌△ACE，

∴BE=CE.

又∵点D是BC的中点，

∴△BED≌△CED.

求证：△ADB≌△ADC.

证明：∵AB=AC，点D是BC的中点，

∴BD=CD，

∴△ADB≌△ADC.

如此一来，八年级学生便会在自主比对正确解题步骤和自身错题解题步骤差异的过程中，更为客观与理性地认识到自己出现错误的主要成因，即“错解一”的错题成因为，找出的全等三角形不全，忽略了△ADB与△ADC；“错题二”的错题成因为，证明题书写格式不规范，不仅将证明三对三角形全等的过程混为一谈，也未将对应的证明条件书写到证明步骤之后；“错题三”的错题成因为，证明三角形全等的条件不足，证明两个三角形全等至少需要三个条件，三个证明过程都仅应用了两个条件，同时能够积极主动地对数学错题进行修正，实现针对性改错与有效避错.

在这一基础上，教师还可设置具有启发性的教学问题：“在数学证明题中，证明三角形全等的基本求证思路是什么？”以此活跃、发散学生的数学解题思维，促使学生从自身的数学解题经验出发，合作梳理与总结归纳出证明三角形全等的一般过程：第一，要观察欲证线段或角存在于哪两个可能全等的三角形中；第二，根据题中已有条件与图形信息，找出两个三角形中三组符合某一判定方法的对应相等条件，证明三角形全等；第三，如果条件不够，便要设法求证所缺条件，进而得到数学解题经验的积累与数学思维能力的锻炼，实现“既知其然，又知其所以然”的有效数学学习.

结 语

总而言之，在义务教育阶段的数学课程教学中，促使学生形成受益终身的数学学科核心素养是最为重要与关键的学科育人目标.在核心素养导向下的初中数学习题讲评课教学中，教师可在充分把握以往数学习题讲评形式、方法、策略等方面存在的问题与不足的基础上，以充分彰显与发挥数学习题讲评于中学生数学核心素养形成发展所起的推动作用为出发点，对习题讲解方式及错题评析方法进行深耕与探微，在切实突出中学生数学学习主体作用与中心地位的同时，使其通过积极参与优质、高效的数学习题讲评，发自内心地感受数学学习的乐趣，并获得数学学习能力及思维能力的进阶.

【参考文献】

[1]黄爱芹.基于“唤醒教学”，上好高三习题评讲课[J].数学之友，2022，36（19）：89-90.

[2]吴渊.引导有方 提高数学习题讲评质量———“双减”背景下数学习题讲评的思考[J].名师在线，2022（26）：55-57.

[3]杨亚平.解题教学要帮助学生“学会寻找思路”———以李庾南老师习题讲评实录为例[J].中学数学，2022（12）：41-42.

[4]杨帆.挖掘习题讲评的深度 拓宽数学思维的广度[J].数学教学通讯，2021（33）：45-46，49.

[5]沈月.习题讲评三顺应，让数学更有味———浅谈初中数学习题讲评策略达成[J].数学教学通讯，2021（20）：62-63.