基于GeoGebra软件构建《高等数学》曲面动态化图形资源

邢维 裴红梅

摘 要：GeoGebra是一款新兴的功能强大的动态数学软件，它可以直观、形象、动态、交互地演示数学中的知识.《高等数学》曲面的教学过程中一般采用的是传统的灌输式方法，忽视曲面动态演示，学生会觉得曲面的知识枯燥乏味，不容易理解.使用GeoGebra软件针对曲面这一节的内容进行动态资源建设，展示旋转曲面、柱面的形成过程，以及常见的二次曲面的截痕，提高学生的学习效果.

关键词：曲面；GeoGebra；动态演示

1 GeoGebra软件介绍

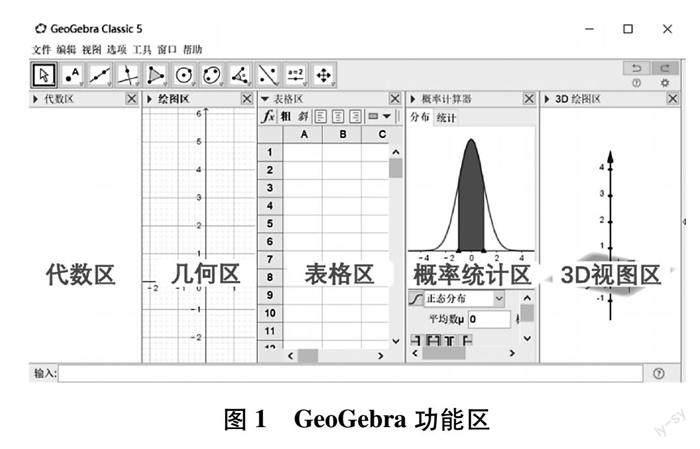
GeoGebra是2002年由美国佛罗里达州亚特兰大大学教授Markus Hohenwarter研发的一款数学软件.它在全球190多个国家中有着广泛的应用，被30多个国家写入中小学的教科书.GeoGebra是由两个英文单词“Geometry”和“Algebra”组合成的，是一款兼具“几何”和“代数”这两个功能的软件.它的优点如下：

（1） GeoGebra是一款具有中文简体版本的免费软件，操作简单，不需要使用者拥有任何编程水平，也不需要学习专门的课程，自己领悟即可.

（2） GeoGebra不仅具有代数和几何功能，还拥有表格、3D计算、概率统计、微积分等功能.GeoGebra是一款功能齐全的动态教学软件，可以导出GIF图像，不需使用视频播放器就可以在PC端使用，方便教学.

（3） GeoGebra具备三维功能，作出的图形不仅直观形象并且交互性强.

2 《高等数学》曲面的地位与教学现状分析

2.1 曲面在《高等数学》中的地位

曲面是《高等数学》的主要内容之一，有着非常重要的地位.曲面的价值有下列几点：

（1） 促进学生理解数形结合的思想，将学过的多元函数和向量等知识联系起来，形成系统的知识体系.

（2） 曲面在《高等数学》中，有着非常重要的作用，曲面的学习为学生后续学习多元函数的微分和积分提供基础知识，使学生更好地计算多元函数微积分问题.

2.2 曲面的教学现状

（1） 在目前的教学模式中，教师的教学方法采用的仍然是传统的灌输式为主的教学方法，不重视演示过程，忽视了学生对曲面思维能力的培养.

（2） 在课堂教学中，学生忽视曲面动态演示，觉得曲面的知识枯燥乏味，不容易理解，接受起来困难.

因此，不难发现曲面教学中存在的问题是教师虽然对知识体系理解深刻，但是信息技术水平有限，导致在课堂教学中一般采用传统的教学方式，以灌输为主，从而让学生感到曲面的知识单调难以理解.

3 GeoGebra软件构建曲面动态化图形

曲面的知识是《高等数学》空间解析几何的重要组成部分.将几何图形用代数语言描述，将几何问题转化为代数问题进行运算，得到结果，再将代数结果转化为几何结论，这就是曲面的核心思想，即数形结合的思想.

教师在讲授曲面的过程中，注重公式方程的记忆，却忽略了知识的生成，使学生对曲面的定义的理解不够透彻，有畏难情绪.

下面设计基于GeoGebra环境下的曲面的动态化图形.

3.1 旋转曲面

定义1：平面上的一条曲线绕该平面上的某一直线旋转一周后生成的曲面叫做旋转曲面，该曲线称为旋转曲面的母線，直线称为旋转曲面的旋转轴.

设曲线C为坐标面yOz上的一曲线，其方程为

f（y，z）=0，

该曲线绕坐标轴z轴旋转一周，得到一以z轴为旋转轴的旋转曲面，其方程为

f（±x2+y2，z）=0.

下面用GeoGebra展示旋转曲面的生成过程.

首先选择一条合适的曲线，其参数方程表达式为

x=0y=t24+1z=t， -2.5≤t≤2.5，

要使用基本语法：曲线（＜表达式＞，＜表达式＞，＜表达式＞，＜参变量t＞，＜起始值＞，＜终止值＞）.在曲线上任意取一个点，使用基本语法：描点（＜对象＞）.这样的点可以在几何对象上任意移动.创建滑动条，使用基本语法：角度，区间最小0°，最大360°，增量1°.打开3D绘图区，在输入框依次输入上述指令.

绘制曲线上的点绕z轴旋转一周之后的轨迹，用滑动条控制动态旋转过程.使用基本语法：曲面（＜曲线＞，＜度|弧度＞，＜直线＞）.这就完成了曲线绕坐标轴旋转一周形成的旋转曲面的动态过程.

控制滑动条，利用GeoGebra动态展示旋转曲面的生成过程，通过动态演示体现曲线上任一点的旋转轨迹和曲线的旋转轨迹之间的关联性，有助于学生形成完整的知识体系.

3.2 柱面

定义2：一条直线L沿着曲线C平行移动后形成的轨迹称为柱面，该曲线C称为柱面的准线，直线L称为柱面的母线.

下面以抛物柱面为例，通过GeoGebra动态展示抛物柱面的生成过程，有助于学生数形结合思想的形成.

设置点C为焦点，直线f为准线，构造一条抛物c.使用基本语法：描点（＜数值列表＞），抛物线（＜点＞，＜直线＞）.滑动条基本语法：数值，区间最小0，最大1，增量0.1.沿着z轴平移抛物线形成抛物柱面，使用基本语法：平移（＜对象＞，＜向量＞），通过控制滑动条，动态演示抛物线c沿z轴平移生成抛物柱面的过程.

3.3 二次曲面

F（x，y，z）=0三元二次方程所表示的曲面叫做二次曲面.通常采用截痕法来研究二次曲面的形状.

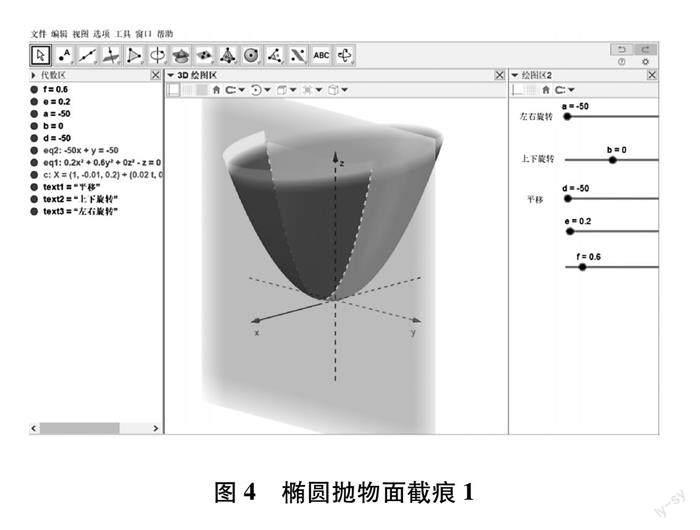
下面以椭圆抛物面为例，通过GeoGebra动态展示用截痕法确定其形状.

椭圆抛物面方程为x2a2+y2b2=z.

GeoGebra绘制椭圆抛物面基本语法：x^2/（a^2）+y^2/（b^2）=z.创建滑动条a和b，基本语法：数值，区间最小-5，区间最大5，增量0.1，滑动条a和b控制椭圆抛物面的“胖瘦”.

通过GeoGebra软件动态演示平面x=m与椭圆抛物面的截痕.基本语法：0*y+x+0*z=m，创建滑动条m，基本语法：数值，区间最小-2，区间最大2，增量0.1.通过控制滑动条m，动态演示平面x=m与椭圆抛物面的截痕为抛物线.

通过GeoGebra软件动态演示平面y=n与椭圆抛物面的截痕.基本语法：y+0*x+0*z=n，创建滑动条n，基本语法：数值，区间最小-2，区间最大2，增量0.1.通过控制滑动条n，动态演示平面y=n与椭圆抛物面的截痕为抛物线.

通过GeoGebra软件动态演示平面z=p与椭圆抛物面的截痕.基本语法：0*y+0*x+z=p，创建滑动条p，基本语法：数值，区间最小0，区间最大2，增量0.1.通过控制滑动条p，动态演示平面z=p与椭圆抛物面的截痕为椭圆.

通过GeoGebra软件的动态演示，可以更好地帮助学生理解椭圆抛物面的概念.

在传统的曲面教学过程中，教师只是将知识灌输给学生，学生总是被动地接受知识，这样不能够帮助学生主动的构建知识.然而利用GeoGebra软件辅助曲面的教学，不仅为学生提供了一个良好的学习环境，同时也促进了学生对曲面知识的主动构建，使学生更好地认识和理解数学知识的本质.

4 总结

利用GeoGebra软件辅助曲面教学可视化效果更好，不仅将概念的形成过程可视化，让学生更好地吸收，同时让学生参与到知识的探索中，培养学生的探索精神和创新思维，增加了课堂的趣味性和学生的活跃性.

参考文献：

［1］ 邓珍珍.GeoGebra辅助初中数学教学的实践研究［D］.合肥师范学院，2018.

［2］ 刘巧玲.GeoGebra辅助高中函数教学的研究与实践［D］.广西师范大学，2014.

［3］ 徐敏霞.基于GeoGebra的高中数学探究教学研究［D］.苏州大学，2016.

［4］ 沈翔.GeoGebra的基本操作指南［M］.北京：高等教育出版社，2016.

［5］ 钱文涛，赵军.GeoGebra软件让数学教学如虎添翼［J］.中国教育技术准备，2014（2）：54-56.

［6］ 同济大学数学系.高等数学（第七版下册）［M］.北京：高等教育出版社，2014.

［7］ 闫永芳.GeoGebra软件在数学分析教学中的应用举例［J］.北京印刷学院学报，2021，29（4）：131-134.

［8］ 姜兆敏，孟凤娟，曹毅.利用GeoGebra辅助高等数学教学的探索［J］.江苏理工学院学报，2023，29（2）：122-128.

［9］ 张敬信.基于GeoGebra构建高等数学动态图形化教学资源库［J］.科技风，2022（3）：142-144.

［10］ 徐阳.GeoGebra助力高中数学可视化教学——以函数教学为例［J］.理科考試研究，2023，30（14）：28-31.

［11］ 周洪.运用GeoGebra着力提升高等数学的教学质量［J］.四川职业技术学院学报，2020，30（5）：116-122.