基于SOLO分类理论的数学核心素养培养研究

马诗　雍龙泉

摘 要：《普通高中数学课程标准（2017版）》提出了六大数学核心素养：数学抽象、逻辑推理、数学建模、直观想象、数学运算以及数据分析.将数学核心素养与SOLO分类理论结合起来进行试题研究，可以更好地理解高考试题的评价功能，进一步发挥高考对数学教学的积极导向作用.本文以2022年全国高考数学乙卷试题为研究对象，基于SOLO分类理论对核心素养下的高考试题特点进行分析，研究其对数学核心素养和思维层次的考查情况，为高中数学教学提供一些新的思考.

关键词：数学核心素养;SOLO分类理论;高考试题;高中数学教学

《普通高中数学课程标准（2017年版）》为展现育人导向，突出数学学科特点，提出了6大数学核心素养［1］.SOLO分类理论作为等级评价理论之一，广泛应用于试题编制和分析，它反映了学生思维所处的层次，一定程度上体现了学生对知识的掌握和应用能力.将“SOLO分类理论”与高中数学核心素养结合起来，可以对高考数学试题结构进行全方位分析，更好地把握高考试题的命题特点.

刘志凤等［2］从核心素养考查的多个方面对2020、2021年高考数学全国卷进行量化分析，得出了新高考过渡期数学试卷的命题特点；覃淋［3］通过构建习题综合难度测量模型，对2022年高考数学全国甲、乙卷理科试题的综合难度进行比较，得出两套高考数学试卷的特点；张鹄［4］以著名数学家波利亚的“怎样解题表”为指引，对2022年高考数学全国乙卷理科第21题的解法进行了探究；张雁冰等［5］通过对2022年五套高考数学试题中的情景化试题进行分析来探索高考试题的特征；杨东等［6］借助思维导图可视化思维的方法对2022年全国甲卷选择题的压轴题进行分析，以此帮助学生厘清题目中的逻辑关系、呈现清晰的思维过程；《中国数学教育》中曹媛［7］、张金良［8］、陆萍［9］、王明海［10］、蒋凤君［11］、郭慧清［12］等人通过对高考专题的解题方法进行不同角度的分析，进而提出了不同专题学习的备考建议；教育部教育考试院［13］对2022年高考数学全国卷试题进行评析，揭示出高考试题注重基础、深入考查核心素养和关键能力.

2022年全国乙卷适用地区包括河南、山西、江西、安徽、甘肃、青海、内蒙古、黑龙江、吉林、宁夏、新疆、陕西.全国乙卷的使用地区相较全国甲卷和新高考卷更多，有一定的普适性，更能体现全国大多数地区的高考试题对学生能力和素养的考查.

通过阅读文献发现以上文章从各个方面对近几年的高考数学试题进行了分析，并从相应的角度给出了备考建议和教学建议，但没有将学生思维所处层次、试题的命制以及核心素养的考查结合起来进行分析. 本文以2022年全国高考数学乙卷为例，基于SOLO分类理论和数学核心素养，通过分析高考数学试卷中所考查的知识点，来判断核心素养以及“SOLO分类理论”处于哪个结构水平，并在此基础上提出几点建议，以期广大数学教师深入了解高考数学试题的能力水平层次，提升课堂教学的效率，促进学生全面发展.

1 SOLO分类理论

SOLO分类理论（Structure of the Observed Learning Outcome），是由教育心理学家比格斯提出的“可观察到的学习结果的结构”.“SOLO分类理论”是指对抽象程度和题目结构上的复杂程度的层次划分，分为5个水平，包括前结构水平、单一结构水平、多元结构水平、关联结构水平和拓展抽象结构水平，其评价指标详见表1［14］.本文将基于“SOLO分类理论”对2022年全国高考数学乙卷部分试题进行层次划分，由于处于“前结构水平”的学生头脑中不具备与问题相关的知识，对问题表现为不知从何下手而猜测试题答案，对于该水平的研究价值不大，因此分析高考试题时只选取后四个结构水平进行分析.

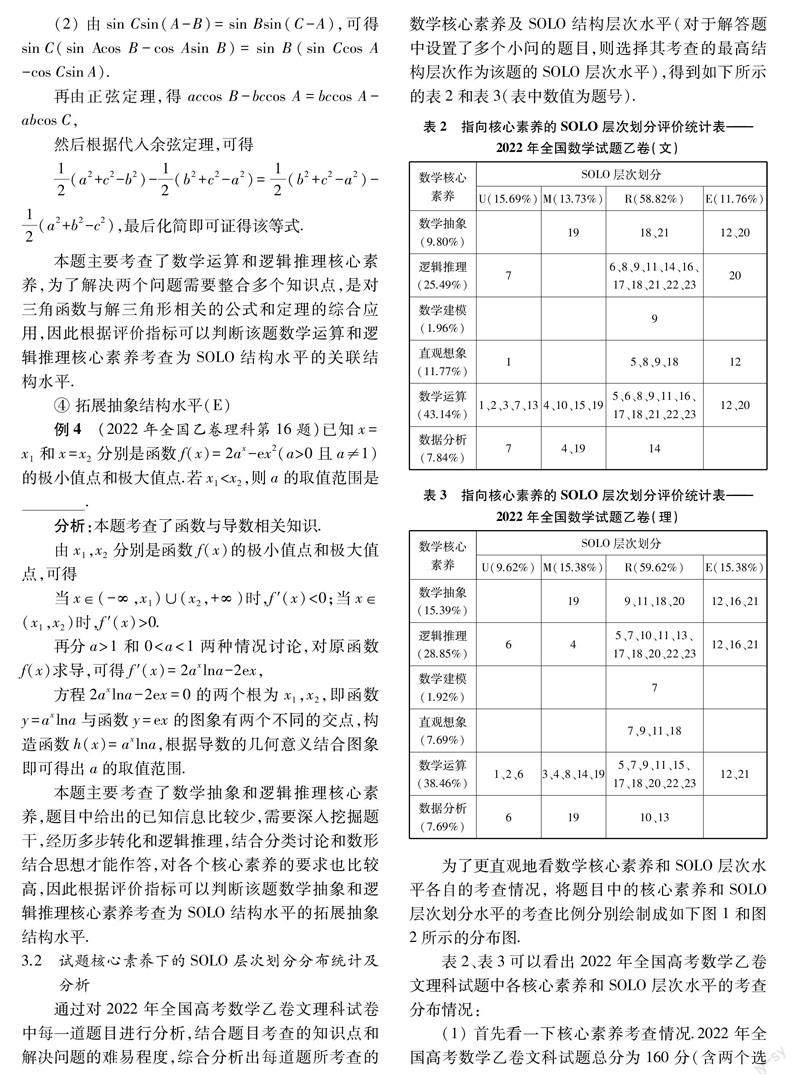
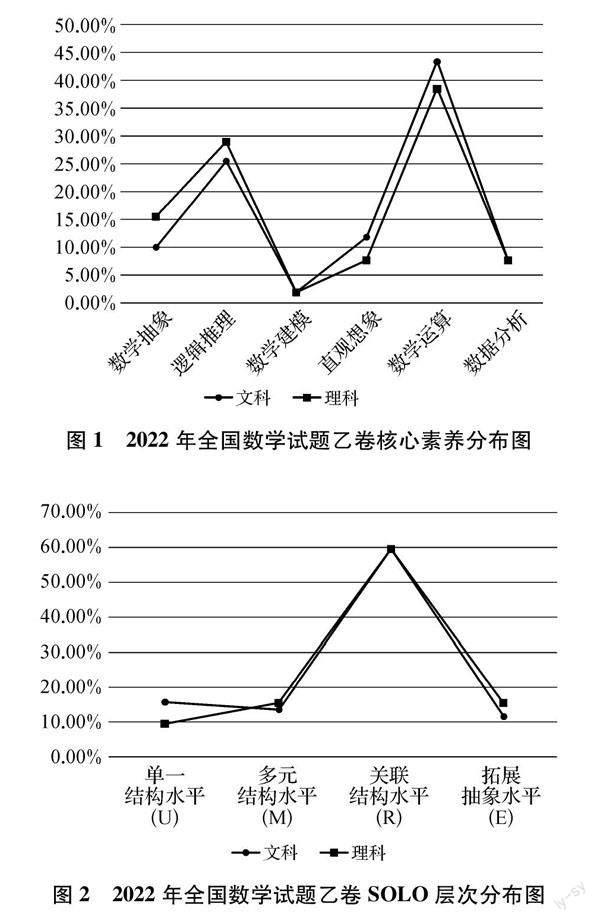
为了更直观地看数学核心素养和SOLO层次水平各自的考查情况， 将题目中的核心素養和SOLO层次划分水平的考查比例分别绘制成如下图1和图2所示的分布图.

表2、表3可以看出2022年全国高考数学乙卷文理科试题中各核心素养和SOLO层次水平的考查分布情况：

（1） 首先看一下核心素养考查情况.2022年全国高考数学乙卷文科试题总分为160分（含两个选做题），各核心素养的考查比重和分值依次如下：数学抽象9.80%，分值约为16分；逻辑推理25.49%，分值约为41分；数学建模1.96%，分值约为3分；直观想象11.77%，分值约为19分；数学运算43.14%，分值约为69分；数据分析7.84%，分值约为12分.2022年全国高考数学乙卷理科试题总分为160分（含两个选做题）各核心素养的考查比重依次是数学抽象15.39%，分值约为25分；逻辑推理28.85%，分值约为46分；数学建模1.92%，分值约为3分；直观想象7.69%，分值约为12分；数学运算38.46%，分值约为62分；数据分析7.69%，分值约为12分.

（2） 接下来再看一下SOLO层次水平考查情况.2022年全国高考数学乙卷文科试题总分为160分（含两个选做题）SOLO层次水平的考查比重依次是单一结构水平（U）15.69%，分值约为25分；多元结构水平（M）13.73%，分值约为22分；关联结构水平（R）58.82%，分值约为94分；拓展抽象水平（E）11.76%，分值约为19分.2022年全国高考数学乙卷理科试题总分为160分（含两个选做题）SOLO层次水平的考查比重依次是单一结构水平（U）9.62%，分值约为15分；多元结构水平（M）15.38%，分值约为25分；关联结构水平（R）59.62%，分值约为95分；拓展抽象水平（E）15.38%，分值约为25分.

图1可以看出，2022年全国高考数学试题乙卷虽然各个数学核心素养都有所涉及，但对这六大核心素养考查的程度极不均衡，主要考查数学运算、逻辑推理、直观想象和数学抽象这4个核心素养，其中数学运算和逻辑推理作为高考考查的方法素养［15］，与数学知识直接关联，是培养学生数学关键能力的必备素养，因此这两个核心素养的占比较高，二者之和约为70%.对数据分析和数学建模2个核心素养的考查很少，这两个核心素养的考查比例加一起不到10%.比较文理科两条折线走势图，可以看出文理科试卷各核心素养考查比重相近，没有明显差异，向着新高考文理科合卷和课程改革的方向发展，可以说文理科又具有一定的统一性.

图2可以看出，2022年全国乙卷高考数学试题SOLO层次水平，虽然四个水平都有涵盖，但其分布也不均衡，这体现出高考作为选拔性的考试，要让不同学生所处的思维层次水平有所区分.通过分析可以得出结论：关联结构水平（R）的比例最高，文理科处于这一层次水平的题目都超过了50%，说明试题在重视学生的基础知识和基本技能的同时，更多地关注学生综合分析问题的能力，凸显了高考试题的综合性和应用性.且前三个层次（单一结构水平U、多元结构水平M和关联结构水平R）占试卷整体的比例超过了80%，由此可以看出文理科试卷都很注重基础知识的考查应用，凸显了高考试题的基础性；而拓展抽象水平（E）下理科的比例略高于文科，该水平对学生的要求比较高，需要学生有一定的创新思维，说明理科试题对学生的创新能力要求更高，凸显了高考试题的创新性.

在进行2022年乙卷文理科试题对比分析时发现，文理科试题相同的比例与往年相比有所上升.周佳婷和朱哲［16］在分析2020年全国Ⅱ卷文理科试题时指出文理科相同的题目共有11道，相同试题的分值共70分.通过对比2022年全国高考数学乙卷文理科试题，可以发现文理科试题均有23道题，其中有13道题相同，包括5道选择题，2道填空题，6道解答题（第17题三角与三角函数第1问，第18题立体几何第1问，第19题概率与统计，第20题圆锥曲线，第22题坐标与参数方程，第23题不等式选讲），分值高达86分，体现了新高考文理科合卷的趋势，为综合改革提前做好过渡和铺垫，助力高考综合改革平稳实施，对高中数学教学与高考数学备考有导向作用［17］.

3 结论和建议

3.1 结论

（1） 2022年全国高考数学乙卷文理科试题对六大核心素养的考查程度表现出不均衡的特点，主要考查了数学运算和逻辑推理这两个数学方法层面的素养，对其他四个核心素养的考查相对较少，而且文理科试题各素养考查比重相近.从SOLO层次水平的划分来看，2022年全国高考数学乙卷文理科试题对SOLO层次水平的考查均表现为文理科试题处于关联结构水平的题目最多，未来高考试题考查可能仍会保持关联结构水平，并且向着创新性和综合性要求更高的拓展结构水平发展.

（2） 2022年全国高考数学乙卷文、理科试题命题趋于统一，文理科试题相同比例较高，相同试题的分值高达86分，并且所考查的知识点基本相同，这是新高考下文理科逐渐合卷的表现.

（3） 2022年全国高考数学乙卷文、理科大部分试题考查了多个核心素养，尤其是解答题，综合性较强，对素养要求也更高.对于SOLO层次水平也有一题考查多个层次水平这样的规律，比如理科卷解答题第17题第1小问，只需要掌握正弦公式、正弦定理和余弦定理，不需要整合这些知识，通过简单的化简就可以证得结论，因此属于多元结构水平的试题，而第2问需要把第1问的结论和余弦定理以及三角形内角和知识点进行整合、推理，才可以求得三角形的周长，因此属于关联结构水平的试题.

3.2 建议

3.2.1 回归教材，重视基础

教材是命题专家的依据，是所有试题的根本.每年高考题中有80%的题目都是基础题和中档题，这两部分主要就是考查学生对课本中基本概念、基础知识、基本方法的掌握情况，高考题干的设问和知识点大多数都与教材中的内容建立起知识链接且关联度较高.2022年全国高考数学乙卷仍和往年一样重视基础，注重考查学生的“四基”“四能”，因此在教学中应该重视教材、用好教材，养成从教材的基础知识出发分析和解决问题的能力.

3.2.2 聚焦素养，提升能力

高考试题对核心素养的考查已经从考查单一的核心素养到多个核心素养的综合运用，对SOLO层次水平的划分集中在关联结构水平，即试题对学生知识融会贯通和整合的能力也有较高的要求.《中国高考评价体系》［18］中提出的“一核四层四翼”，明确了高考考查的基础性、综合性、应用性和创新性，这些特点都指向数学素养，直达关键能力.

高考试题在考查学生基础知识、基本技能、基本思想和基本活动经验的同时，还需要运用观察和类比、归纳与猜想、推理与运算等数学活动来提升学生发现问题、提出问题、分析问题和解决问题的四大能力，以达到培养学生的高阶思维的目的，而高阶思维作为核心素养的集中体现，说明了培养学生数学核心素养和数学关键能力的重要性.教师在知识教学中应着重培养学生的数学抽象和直观想象素养，在解题教学中注重培养学生的逻辑推理和数学运算素养，并把数据分析和数学建模素养贯穿在知识和解题教学中［15］.

3.2.3 引导教学，把握课堂

高考试题对处于关联结构水平的考查较多，教师在教学中要帮助学生搭建知识体系，加强知识之间的关联性，培养学生对知识的融会贯通和整合能力，注重对知识的综合应用，凸显高中数学知识的深度和广度，同时还要培养学生的逻辑思维和创新精神，这也是高考对于拓展抽象水平层次的考查要求.在教学中，为了给处于不同SOLO层次水平的学生提供不同的思维模式， 可以运用举一反三、一题多解等教学方法，这样既能提升学生的学习兴趣，又能实施因材施教.

3.2.4 研读《课标》，与时俱进

《课标》作为高考命题的纲领性文件之一，对把握命题方向起到了很好的指引作用.2020年发布的《普通高中数学课程标准（2017年版2020年修订）》［19］对课程内容和结构等方面做了一定的调整，这都给高考数学的复习备考提供了参考，因此在教学中要反复研读，把握变化，将课标内容和教材紧密结合，从而提高教学效率.

参考文献：

［1］ 中华人民共和国教育部. 普通高中数学课程标准（2017年版）［M］.北京：人民教育出版社，2018.

［2］ 劉志凤，李珂，张玉环.核心素养视角下2020、2021年14套高考数学试卷的比较分析［J］.中学数学教学参考，2022，855（13）：62-66.

［3］ 覃淋.基于习题综合难度模型的高考数学试题难度比较——以2022年全国甲卷、乙卷理科试卷为例［J］.课程教学研究，2022，128（8）：21-30.

［4］ 张鹄.对2022年高考数学全国乙卷理科第21题的探究与思考［J］.数学通讯，2022，883（14）：53-56.

［5］ 张雁冰，李健，吕天玺.2022年高考数学情境化试题的特征分析［J］.中学数学杂志，2022，397（11）：49-53.

［6］ 杨东，李洪全，姜远航.借助思维导图将思维“可视化”，解决压轴题——以2022全国甲卷第12题为例［J］.中学数学，2023（1）：3-6.

［7］ 曹媛，李金生.重视基本概念原理 强调数学思维方法——2022年高考“集合、常用逻辑用语、不等式”专题解题分析［J］.中国数学教育，2022：21-31+40.

［8］ 张金良，高玉良.紧扣教材·突出本质·彰显素养——2022年高考“函数与导數”专题解题分析［J］.中国数学教育，2022：32-40.

［9］ 陆萍，王剑.重视逻辑推理 关注全局变化——2022年高考“三角函数与解三角形”专题解题分析［J］.中国数学教育，2022：41-47+57.

［10］ 王明海，刘连杭，张晓斌.彰显函数特性 渗透数学思想——2022年高考“数列”专题解题分析［J］.中国数学教育，2022：48-57.

［11］ 蒋凤君，金克勤.指向核心素养的高考概率与统计试题新变化——2022年高考“概率与统计”专题解题分析［J］.中国数学教育，2022：86-96.

［12］ 郭慧清，黄文辉，葛一伟.映山红盛开，夜亦是红色——2022年高考数学试题解题分析及复习备考建议［J］.中国数学教育，2022：3-20.

［13］ 创设情境 发挥育人作用 深化基础 考查核心素养——2022年高考数学全国卷试题评析［J］.中国考试，2022，363（7）：14-19.

［14］ 鲍建生，周超.数学学习的心理基础与过程［M］.上海：上海教育出版社，2009.

［15］ 宁锐，李昌勇，罗宗绪.数学学科核心素养的结构及其教学意义［J］.数学教育学报，2019，28（2）：24-29.

［16］ 周佳婷，朱哲.基于数学核心素养的高考数学试题分析——以2020年全国Ⅱ卷高考数学试题为例［J］.数学教学研究，2021，40（4）：40-45+54.

［17］ 白兴宏，张炳意.基于数学学科核心素养视角的高考数学试题分析——以2018年全国Ⅱ卷高考数学试题为例［J］.数学教学研究，2019，38（2）：52-55.

［18］ 教育部考试中心. 中国高考评价体系［M］.北京：人民教育出版社，2020.

［19］ 中华人民共和国教育部.普通高中数学课程标准（2017年版2020年修订）［M］.北京：人民教育出版社，2020.

基金项目：陕西高等教育教学改革研究项目“跨校跨专业教研联合体探索”（项目编号：21BZ013）.