精心选编经典问题，教会学生深度思考

葛媛

摘 要：三角形“四心”（内心、外心、重心、垂心）的几何专题课如何走向“刷题式”复习，是值得开展教学研究的一个问题.本文从尺规作图出发，当作出三角形两条角平分线之后，仅用直尺补出第三条角平分线，并追问作图依据；接着在三角形两条边垂直平分线交于一点，两条高线交于一点之后，提出同样的补图要求，可以让学生在“学解题”过程中学会“深度思考”.

关键词：三角形的“四心”；专题课；学解题；深度思考

近期笔者参与了两所学校中考复习教学研讨活动，两次执教了相同课题《三角形的“四心”》，对这类专题复习课有了较为深入的思考.现将该课教学设计整理成文，并跟进教学思考，提供研讨.

1 三角形的“四心”专题课教学设计

活动（一） 尺规作图

问题1：在三角形ABC中，根据要求作图.

（1） 作△ABC的角平分线BE；

（2） 作△ABC的边BC的垂直平分线OE，垂足为E（保留作图痕迹）；

（3） 作△ABC的高AD（保留作图痕迹）.

教学组织：先让学生独立作图，然后安排学生上台讲解作法及依据，巩固基本作图，并进一步指出，重复上述操作，可以继续作出三角形另外的角平分线、边的垂直平分线、高线.

活动（二） 直尺作图

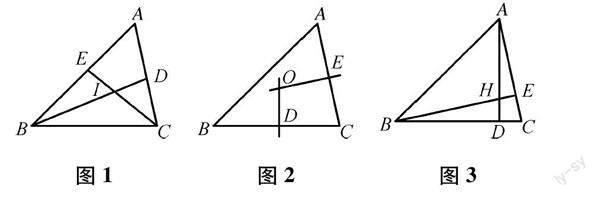
问题2：如图1，△ABC的角平分线BD，CE相交于点I；△ABC的两边垂直平分线OD，OE相交于点O；△ABC的高AD，BE相交于点H.

（1） 不使用圆规，只使用直尺，在图1中补出△ABC的角平分线AF，并说明理由；

（2） 在图2中，连接AD，BE交于点G，射线CG交AB于点F，求证：直线FO垂直平分AB；

（3） 在图3中，直线CH交AB于点F，求∠AFC的大小.

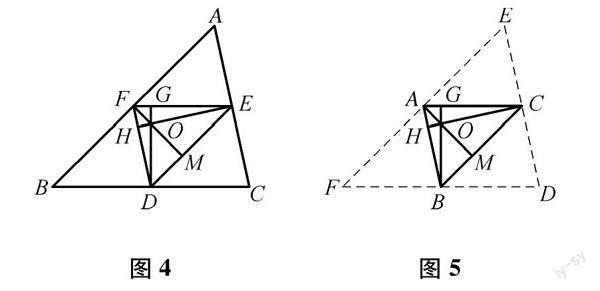
教学组织：第（1）问主要是让学生根据三角形三条角平分线交于一点，补出第三条角平分线，学生补图之后，教师要追问学生如何证明.第（2）问证明的关键步骤之一是点O到顶点A，B的距离相等；另一个关键步骤是F为AB的中点.为了证后一步骤，可先利用三角形三条中线交一点（重心）来证明F是AB的中点.在证明这一小问时，同时出现了三角形ABC的外心和重心.继续求解第（3）问时，出现三角形的三条高交于一点（垂心），本课研究的“四心”全部出现.需要指出的是，学生如果在八年级学习“平行四边形”一章时没有解决过如何证明三角形的三条高交于一点，教师可以提供以下铺垫式问题启发思路.如图4，连接△ABC的三边中点的三角形DEF，结合三角形中位线性质，△ABC的三边垂直平分线与△DEF的三边交于G，H，M三点，可得△DEF的三条高DG，EH，FM交于一点O.受到该图的启发，可将图3中的△ABC看成是图4中的△DEF，构造辅助线（如图5）解决问题，分别证出A，B，C是三角形DEF的各边中点，利用△DEF的三边垂直平分线交于一点O，说明△ABC的三条高交于一点.至此，三角形“四心”及其性质都通过师生对话进行了复习和证明.如果学生证明三角形三条高交于一点，采取“四点共圆”的思路，也可鼓励学生上台讲解.

活动（三） 解题运用

问题3：如图6、图7，△ABC中，AC＝3，BC＝4，AB＝5.

（1） 如图6，⊙I内切于三角形ABC中，求⊙I的半径.

（2） 如图7，点G，I分别是△ABC的重心、内心，连接GI，求GI的长.

教学组织：第（1）问相对基础，可以鼓励学生从不同的角度列方程（组）解决问题；第（2）问具有挑战性，关键步骤之一是内心I到三边距离为1（对应着上一问的结论），接着求出点G到边BC的距离为1，从而得出GI∥BC，再求出重心G到边AC的距离为4/3，于是GI长为4/3-1＝1/3.

2 关于几何专题复习的教学思考

2.1 几何专题备课学材选编要注重关联

几何专题教学没有现成的教材可以使用，教师在构思几何专题教学前要精心选编学材，入选问题要围绕几何专题的教学主线，前后教学环节要力求逻辑连贯、过渡自然.比如在上文课例中，我们选定的专题是三角形的“四心”，全课选编的学材都贴近教学主线、渐次变式、相机拓展，前序教学活动又给后续较难问题的思路带来启发.教师在引导、追问或点评时，也应尽可能贴近主线展开，使得全课主题聚焦、重点突出.

2.2 几何专题教学要帮助学生“学解题”

涂荣豹教授指出：“数学解题教学的任务，学生的主要任务并不是解题，而是‘学解题.并且通过学解题‘教学生学会思考”［1］.几何专题教学并不能满足几道同类习题的解决，而要精心选编同类习题，并恰当呈现，让学生在研究铺垫问题、同类问题、拓展问题之后自主感悟出本课专题的解题关键，从而达到在学习解一道题或同类问题之后，学会解题、学会思考.宁连华教授进一步指出“教学生学会思考”的质量提升策略是“教在起始点”“教在类比处”“教在反思处”［2］.比如，上文几何专题教学课例中，我们课堂起点设置得很低，人人参与、尺规作图，让学生知道三角形“四心”与基本尺规作图之间的关系，随后限制作图工具，增加作图难度，学生需要想清“仅用直尺补图”的依据.还有，几何专题课也要特别注重视课堂小结的设计，要精心预设小结问题，引导学生学会反思回顾，包括本课重点学习内容、解题策略或者具体到某道问题的关键步骤与易错点等等.

2.3 几何专题教学要教会学生深度思考

宁连华教授就学生在高考数学答题素养上的不足曾指出“想得不深，变得不当，算得不好，写得不精”，并建议数学教学要重视以下四点：“教深度思考，教合理变换，教运算思维，教精准表达”［3］.以上文关注的几何专题教学为例，圍绕一类经典几何问题，通过铺垫问题、变式问题、拓展问题的渐次呈现，促进学生想得更深.具体来说，当学生能作出三角形一条角平分线之后，不再安排“重复”作第二条、第三条角平分线，而是直接给出两条角平分线交于一点，然后限制作图工具，仅使用直尺继续补出第三条角平分线，这样的设计促进了学生的深度思考，让学生在作图中学会求简、求优.考虑到已知三角形两条边的垂直平分线交于一点，仅使用直尺补出第三边的垂直平分线有较大的难度，所以我们提供一种补图方法，让学生读句补图，并思考作法依据，在“深度思考”与“教学用时”之间找到一个平衡.当然，如果学情较好，也可直接安排学生先独立探究这类较难作图题.对于三角形的两条高线交于一点，补出第三条高，仅用直尺作图不难，难在如何证明“三角形三条高交于一点”，可以先安排学生独立思考，再分组各自证明进展，教师参与小组交流，率先获得进展的小组选派代表上台展示证明方法，教师通过追问促进学生精准表达.

参考文献：

［1］ 涂荣豹.数学教学设计原理的构建——教学生学会思考［M］.北京：科学出版社，2018.

［2］ 顾锋，宁连华.于无疑处教有疑［J］.数学通报，2022，61（7）：35-38.

［3］ 宁连华.指向核心素养的数学高考评价及教学转向审思［J］.中学数学月刊.2022（11）：1-4.