精心设计问题链 以生为本促“双减”

刘建

【摘要】随着“双减”政策的逐步落实，学生的作业负担和校外培训负担明显减轻.为了做到减负提质，提高课堂教学效率成为关键.课堂中，教师通过精心设计问题链，对学生进行启发引导，把学习的主动权交给学生，让学习真正发生，体现以生为本，从而实现课堂效率和教学质量的提高.

【关键词】问题链；以生为本；“双减”

【基金项目】江苏省中小学教学研究第14期立项课题“初中数学‘链+课堂的实践研究”（2021JY14-L398）.

一、教学背景

如皋市吴窑镇吴窑初级中学一直坚持落实立德树人这一根本任务，打造“爱的教育”品牌，鼓励全体教师做有温度的教育，当有情怀的教师.“双减”之后，学生的作业负担和校外培训负担确实明显减轻，但减负并不是“双减”的最终目的，让学生在学校里就能学足学好，提高学校教学质量才是“双减”政策的目标.学校教学的主阵地在课堂，因此切实提高课堂教学效率成为落实“双减”政策的关键.

在课堂中以生为本，把学习的主动权交给学生，让学习真正发生，这就是“爱的教育”的真正体现.笔者认为，教师通过精心设计问题链，对学生不断进行启发引导，就能让“以生为本”落到实处，让“双减”政策落地落实.文章拟以人教版八年级上册“14.2.1平方差公式”的教学为例，浅谈“双减”背景下数学课堂如何做到以生为本.

二、教学目标

本节课是“14.2乘法公式”的起始课，因此笔者将本节课的教学目标设置为：

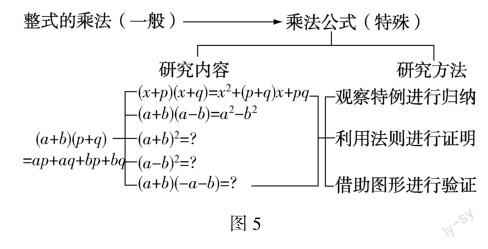
（1）通过回顾特殊形式的多项式相乘，展望乘法公式单元的研究内容和研究方法，构建乘法公式单元知识体系，丰富数学活动的经验和体验.

（2）通过平方差公式的发现、推导、验证和应用，使学生体悟知识方法的生成过程和应用价值，激发学生的主观能动性，进一步培养其逻辑思维能力和推理论证能力.

三、教学设计

（一）从一般到特殊，展望研究内容

问题2：仔细观察这些式子，两个括号中的多项式有什么联系和区别？你认为多项式与多项式相乘有哪些特殊形式？（先独立思考，再小组交流）

生2：（a+3b）（a-3b），两个括号中的多项式一项相同，另一项互为相反数，这样的式子形如（a+b）（a-b）.

生3：第2题所有式子两个括号中的多项式一项相同，另一项不同，这样的式子形如（x+p）（x+q）.

问题3：结合平时完成的练习，两個项数为2的多项式相乘还有其他特殊形式吗？

生4：（a+b）2.

生5：（a+b）（-a-b）.

【设计意图】乘法公式的运用是在学生已经学过整式乘法的基础上进行的，从一般的多项式乘多项式出发，教师让学生寻找其特殊形式，在回顾旧知的基础上对即将研究的内容进行展望，让学生在学习之前对整个单元有一个整体概念，同时在此过程中也渗透了分类讨论和从一般到特殊的数学思想方法.

（二）借助已有方法，开展公式探究

1.观察特例，归纳规律

问题4：今天我们研究第二个式子（a+b）（a-b），请同学们举几个符合该特征的式子，并利用多项式与多项式相乘的法则计算出结果.

生6：（x+2）（x-2）=x2-4.

生7：（1+3a）（1-3a）=1-9a2.

生8：（x+5y）（x-5y）=x2-25y2.

问题5：观察上述等式，你发现了什么规律？

（一段时间后，教师发现不少同学还存在疑问，于是设置子问题进一步启发引导.）

子问题1：等式左边的式子有什么特征？

生9：等式左边两个括号中的第一个数和第二个数都相同，中间的符号不同.

生10：等式左边是两个数的和乘这两个数的差.

生11：等式左边两个括号中的两项，一项相同，另一项互为相反数.

生12：等式左边可以写成（a+b）（a-b）的形式.

子问题2：等式右边的式子有什么特征？

生13：等式右边的两项是两个数平方的差.（师：即两个数的平方差.）

生14：等式右边的第一项是等号左边括号中第一个数的平方，等式右边的第二项是等号左边括号中第二个数的平方.

生15：等式右边可以写成a2-b2的形式.

子问题3：你能用文字或符号总结这一规律吗？

生16：用文字可以表述为：两个数的和与这两个数的差的积，等于这两个数的平方差.

生17：用符号表述为（a+b）（a-b）=a2-b2.

【设计意图】有前面学习的经验，无论是举符合特征的例子，还是观察所得等式归纳规律，对学生来讲都属于最近发展区里的内容，这些都可以由学生自己完成.在学生回答某些问题存在困难时，教师要设置子问题，铺设台阶，进一步启发引导.教师让不同的学生用不同的表达方式尝试归纳规律，能有效让所有学生逐渐加深对公式的理解.

2.运用法则，证明公式

问题6：这个等式就能作为公式使用吗？（大部分学生迟疑）

追问：刚才我们是怎样得到这个等式的？

生18：我们是通过观察几个特殊例子总结得出上面的等式的.

生19：哦，几个特殊例子不能代表所有的式子.

生20：我们也不可能穷尽所有这样的式子，所以我们必须想办法给出证明.

问题7：那么我们应该如何证明呢？（学生独立完成，然后小组交流）

生21：我们可以利用多项式与多项式相乘的法则进行（a+b）（a-b）=a2-ab+ab-b2=a2-b2.

生22：我们还可以利用公式（x+p）（x+q）=x2+（p+q）x+pq进行，（a+b）（a-b）=a2+（b-b）a-b2=a2-b2.

追问：为什么可以用第二种方法证明？

生23：今天所学的（a+b）（a-b）不仅是（a+b）（p+q）的特殊形式，还是（x+p）（x+q）的特殊形式.

师：通过证明，该等式是成立的，我们把这个公式称为平方差公式.

【设计意图】学生对于证明的必要性很模糊，对于代数证明的必要性则更加模糊.教师通过提问和追问，让学生明白通过观察特例归纳出来的结论未必正确，必须经过严格证明才行.公式证明对于学生来讲相对较为容易，这里主要是让学生进一步体会一般到特殊的数学思想方法，一般形式所具有的方法特殊形式一定具有.

3.构造图形，验证公式

问题8：你能构造出图形说明平方差公式吗？（学生思考片刻，但很多同学没有头绪）

追问1：前面我们是怎样利用图形面积的方法说明公式（x+p）（x+q）=x2+（p+q）x+pq的？

生24：构造出图1中的图形，把等式左边看成长为（x+p），宽为（x+q）的长方形的面积，右边则是4个小长方形的面积.

追问2：那么平方差公式的左右两边的这些式子可分别看成哪些图形的面积？

生25：（a+b）（a-b）可看成长为（a+b），宽为（a-b）的长方形的面积.

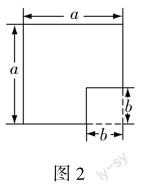
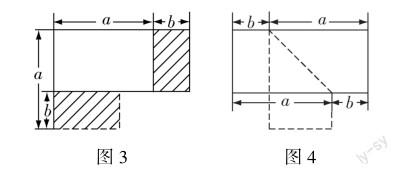
生26：a2可看成边长为a的正方形的面积（教师拿出边长为a的正方形模型），b2可看成边长为b的正方形的面积（教师拿出边长为b的正方形模型，其中b

追問3：那么平方差公式右边可以理解成什么图形的面积？

生27：可以理解为从大正方形中减去小正方形后所得图形的面积.

（师生用剪刀进行操作并在黑板上画出图2）

追问4：对照等式左边，接下来需要干什么？

生28：把这个图形剪拼成一个长为（a+b），宽为（a-b）的长方形.

追问5：请同学们动手画一画，想一想应该如何剪拼？

生29：如图3，我们可以剪掉阴影部分的长方形，再补到右边，从而得到符合要求的长方形.

生30：如图4，我们可以剪下虚线部分的梯形，再把两个梯形拼成如图所示的长方形.

【设计意图】问题8难度较大，笔者并没有直接给出课本中的图，而是首先回顾已学公式的图形面积验证方法，然后让学生模仿、类比，由式思形，再让学生进行剪拼，把整个构造图形的过程全部交给学生.教师不越俎代庖，所起的作用仅是启发引导.让学生独立构造有一定难度，教师需要通过不断追问，引导学生回忆相关旧知，领悟方法，铺设台阶，动手操作，启迪思维，并利用不同的方法解决问题.

（三）通过小结提升，继续展望新知

问题9：通过这节课的学习，你有哪些收获？（略）

问题10：你觉得我们接下来将研究什么？（略）

本节课部分板书如下：

【设计意图】教师通过小结，让学生巩固所学知识，知道使用平方差公式的注意事项，进一步强化乘法公式的研究方法，了解接下来需要研究的内容.在本节课中，教师设计了一些不可以运用平方差公式的问题，让学生认识到它们也具有特殊性，利用本节课的研究方法学生可以开展独立探究.本节课的板书设计有利于学生构建乘法公式单元的知识体系.

四、教学反思

（一）把学习的主动权还给学生

本节课中教师通过精心设计的问题链，不断启发引导学生，在与学生反复问答、深层互动中，水到渠成地生成知识和方法.知识方法是在启发过程中自然生成的，不是教师反复敲黑板告诉学生的，学生真正理解了，因此不容易遗忘.在不断启发中学生搞清了知识方法的来龙去脉，重视知识方法的生成过程；在不断启发中教师了解学生的实际情况，然后对症下药，针对学生出现的问题及时调整教学思路；在不断启发中教师引导学生思考，启迪学生的智慧，从而实现“培优”；在不断提问、追问中，教师夯实了学生的知识基础，从而实现“补差”.因此，这样的课堂真正体现了以生为本，让每一名学生在课堂中都能学有所获，都能得到应有的进步，真正体现了教师对每一名学生的关爱.

（二）有利于优化学生认知结构

问题1至问题3通过寻找特殊形式的多项式相乘，使学生明确“乘法公式”单元的研究内容，问题4至问题8借助于已有的研究方法，展开对平方差公式的探究，问题9至问题10让学生通过议论、小结和提升，达到准确运用平方差公式的目的并展望即将学习的内容.这样做既有助于学生知识结构的整体形成，也有利于学生对运用平方差公式进行计算的整体把握.

【参考文献】

[1]中华人民共和国教育部.义务教育数学课程标准（2022年版）[M].北京：北京师范大学出版社，2022.

[2]印冬建.初中数学“链+”课堂的建构与思考：以“15.1.1从分数到分式”为例[J].中学数学，2020（16）：17-20.

[3]黄骥飞.巧借分层变式提升学习能力：以“平方差公式”的教学设计为例[J].数学大世界（上旬），2022（12）：30-31.