追求算理一致性的“小数除法”单元整体设计与实践

朱曙光　王国建

［摘 要］单元整体设计是优化单元知识的教与学的过程，是课程整合的基本形式之一。通过对“小数除法”这一单元内容进行纵横分析，并在此基础上建立单元内外知识之间的联系，从而对单元的课时内容进行更为合理的布局，进而在教学中实现单元教学目标，凸显算理的一致性。

［关键词］算理；一致性；小数除法；整体设计

［中图分类号］ G623.5［文献标识码］ A［文章编号］ 1007-9068（2023）35-0036-03

“小数除法”是人教版教材五年级上册第三单元的教学内容，其中，掌握小数除法的算法和算理是本单元教学的重点。笔者从单元整体的角度出发，提炼核心概念，对单元的教学内容进行整体性设计，沟通小数除法与整数除法之间的联系，打通单元内部知识的脉络，进而让学生感悟算理的一致性。

一、横纵分析，整体构建单元知识体系

1.横向分析——找准各课时之间的联系

在同一个教学单元中，各个课时的知识内容之间存在着密切的联系，这些知识点相互衔接，共同组成一条知识链。

学习小数除法的前提是掌握整数除法和小数的意义。“小数除法”整个单元以“除数是整数的小数除法”为起始课，“一个数除以小数”是“除数是整数的小数除法”的变式，其他内容则是这两种除法的商的多种情形与应用。可见，掌握小数除法的算法和算理是本单元的重点。小数除法的算理和算法与整数除法大致相同，唯一不同的是小数除法需要考虑小数点。因此，本单元教学的核心要义是将整数除法的算理和算法迁移到小数除法中。

2.纵向分析——明确单元的地位与作用

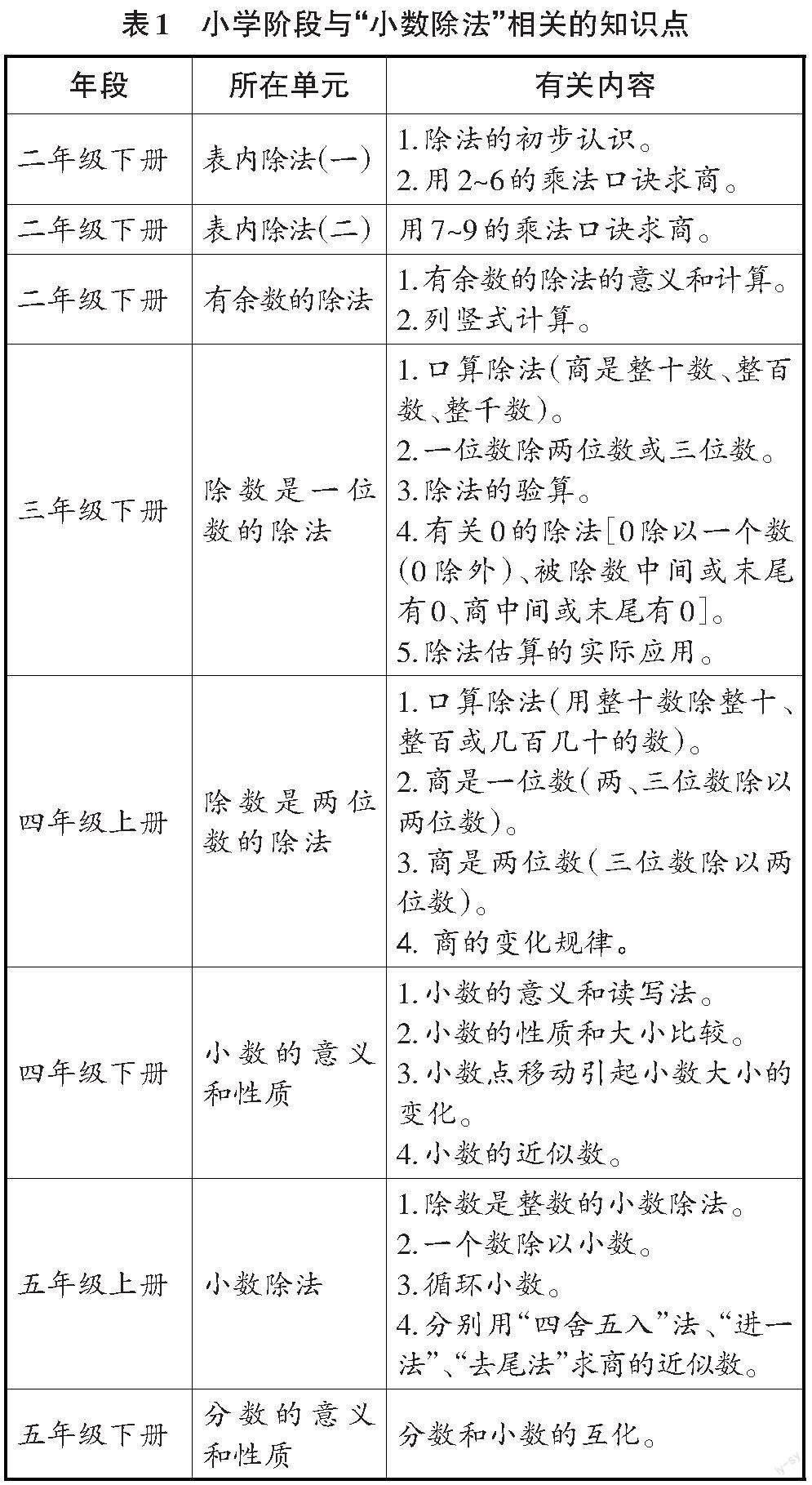
教师梳理与对比所有相关的单元，厘清教学的前后顺序，寻找知识的发展脉络，了解本单元在整个知识体系中的作用。这有助于教师明确本单元的教学目标与重难点，明确之前的教学内容对开展本单元教学的影响。同时，教师需要明确本单元的知识应该掌握到什么程度，才能有序推动整个知识体系的构建。笔者对小学阶段与“小数除法”相关的知识点进行了梳理（见表1）。

从表1中可以看出，“表内除法（一）”是学生学习小数除法的起点，小数除法的学习建立在整数除法的基础上。因此，对整数除法算法和算理的掌握情况将直接影响小数除法的学习。

二、合理布局，重新构建单元教学内容

1.基于核心概念，确定单元教学目标

“一个数除以小数”是基于“除数是整数的小数除法”的迁移，而“除数是整数的小数除法”是基于“整数除法”的迁移，归根结底，“一个数除以小数”是基于“整数除法”的迁移。由此，笔者确立了“小数除法”的单元与课时核心概念（见表2）。

基于以上分析，笔者从知识技能、意义理解、思想方法和情感态度四个方面来描述单元教学目标（见表3）。

2.基于横纵梳理，调整单元课时内容

根据对知识内容的横纵梳理，笔者对“小数除法”的单元教学进行了整体重构，将新课教学分成四个板块，分别是“除数是整数的小数除法”“一个数除以小数”“循环小数与算式规律”和“商的选择与应用”。在重构后的教学设计中，笔者将原先的“商的近似数”教学内容调整至“循环小数”和“用计算器探索规律”之后，并将这三种求商近似数的方法整合到同一教学板块中。具体构思见表4。

这四个教学板块中，第一、第二个板块两种小数除法是本单元的教学重点。第三个板块是在计算小数除法的基础上，进一步探讨商的另一种形式——循环小数，并探究算式中商的规律。第四个板块是引导学生在解决问题时根据实际情况灵活选择“四舍五入”法、“进一法”或“去尾法”来处理商。

三、整体设计，精准落实单元教学目标

1.单元导读，整体感知基本内容

单元导读可以帮助学生明确单元学习的重点，理解单元知识点之间的关联以及它们与之前所学知识之间的联系。

单元导读可以这样安排：

（1）初读单元内容，本單元主要学习哪些知识？

（2）再读单元内容，你觉得本单元的知识之间存在怎样的联系？哪几个知识点之间的联系最密切？本单元学习的内容跟之前学习的什么内容有关？

“小数除法”的单元导读有助于学生从整体上把握整个单元的知识脉络与学习内容，使学生对小数除法的知识结构形成初步认知。

2.分步学习，自然建构知识体系

（1）在比较中沟通知识的“联”

“除数是整数的小数除法”是“小数除法”单元的起始课，它的学习以整数除法为基础，因此，教师在教学中应以整数除法为切入口，通过联系整数除法和小数除法来激活学生的思维，促进知识的正向迁移，实现前后知识的自然对接。这样，单元的起始课便有了学习的着力点。

[例题]王鹏坚持晨练，计划4周跑步22.4km，他平均每周应跑多少千米？

学生都列出了算式“22.4÷4”，具体计算时出现了5种方法（如图1）。

①22.4km=22400m，22400÷4=5600m=5.6km

②22.4÷4=20÷4+2.4÷4=5+0.6=5.6km

③22.4÷4=5.6   ④22.4÷4=5.6   ⑤22.4÷4=5.6

笔者引导学生对这5种方法进行三次比较，以便学生发现整数除法和小数除法之间的联系和区别，实现算理和算法的迁移，从整体上认识除法运算，将除法运算的知识融会贯通。

比较一：这些方法中哪几种比较相似？请按照方法的相似性将它们归类。

比较二：观察方法4和方法5，在一步一步除的时候，下面到底是写2.4还是24？

比较三：为什么方法5的商有小数点，方法3的商没有？小数点该怎么点？

新知的学习建立在旧知上，通常需要对旧识进行正向的迁移。转化正是实现正向迁移的重要方式。转化的实现需要教师引导学生进行比较、辨析，发现知识之间的内在联系。

（2）在转化中凸显知识的“通”

将已学的单元知识迁移到新授单元的知识学习中，让学生感受知识间的相通性，不仅有助于学生巩固旧知识，还有助于学生更好地理解新知识，从而更灵活地运用所学知识。

[例题]奶奶编“中国结”，编一个要用0.85m丝绳。用7.65m丝绳可以编几个“中国结”？

笔者首先组织学生围绕“7.65÷0.85与我们学过的小数除法有什么不同”这一问题展开探究和交流。然后，阐述小数除法的基本方法，将除数是小数的小数除法转化为除数是整数的小数除法，即利用商不变的性质将“7.65÷0.85”转化为“765÷85”。最后，让学生根据除数是整数的小数除法的算法进行计算。通过转化让学生体会到两种小数除法之间的联系，实现知识的自然过渡，从而帮助学生更全面地理解和掌握小数除法的计算方法。

（3）在衔接中体现知识的“顺”

在单元教学中，教师应将单元内的知识串成一条知识链，从一个知识点过渡到另一个知识点的教学应自然，体现单元知识点衔接的顺畅性。

[例题]爸爸要给王鹏买羽毛球，羽毛球一筒19.4元，有12个。

（1）每个羽毛球大约多少钱？

（2）爸爸带了115元钱，可以买多少筒？

（3）王鹏将用过的羽毛球放回球筒中，65个羽毛球要几个球筒才能装完？

“商的近似数”的教学内容涉及循环小数，因此笔者将此内容的学习调整到“循环小数”之后。在这一课的教学中，笔者出示上述例题让学生列式计算。学生计算第（1）题后发现商是一个循环小数，笔者顺势提问：“在现实生活中，钱数可以是循环小数吗？”学生马上意识到，题目问的是“大约多少钱”，要用“四舍五入”法求商的近似数。在学生掌握了用“四舍五入”法求商的近似数之后，笔者继续提问，引导学生思考和探讨不同情况下求商的近似数的方法。

在“雙新”背景之下，对单元整体教学进行研究是大势所趋。无论单元知识属于哪一个知识体系，单元整体设计中对教材处理的基本原则都是提炼核心问题、确定整体目标、关注前后内容、确定单元课时，在知识与知识的关联中凸显数学原理的一致性与整体性。

［ 参 考 文 献 ］

[1] 张丹.数与代数应用问题的内容主线和教学建议[J].小学数学教师，2010（7）：45-82.

[2] 邵汉民.重构顺序分解难点：“角的度量”单元整体重构与预学作业的设计[J].教学月刊小学版（数学），2017（Z2）：40-43.

[3] 邵汉民.“预学后教”策略下关注“联系”的期末复习：以“小数乘、除法”复习为例[J].小学数学教师，2015（1）：54-58.

[4] 人民教育编辑部.教学大道：写给小学数学教师[M].北京：高等教育出版社，2010.