基于结构化“数的运算”单元整体教学实践研究

王锐利

［摘 要］《义务教育数学课程标准（2022年版）》将“数的认识”和“数的运算”两个主题整合为“数与运算”主题，凸显了数学学科内容的整体性和结构性，也更好地体现了学科本质，强化了数的运算与数的概念的一致性。作为“数与运算”主题内容的子主题，“数的运算”单元整体教学不仅需要遵循“概念本质和算法的一致性”“基本活动经验的一致性”和“数学思维方式及其抽象水平的一致性”三个原则，还需要依次具体落实“从结构化主题提炼大概念”“明确单元学习目标和学习评价体系”“确定单元关键问题”和“设计单元学习任务序列”四个步骤。

［关键词］数；运算；一致性；单元整体教学

［中圖分类号］ G623.5［文献标识码］ A［文章编号］ 1007-9068（2023）35-0029-05

《义务教育数学课程标准（2022年版）》（以下简称《2022年课程标准》）延续了《义务教育数学课程标准（2011年版）》（以下简称《2011年课程标准》）对领域的分类，仍为“数与代数”“图形与几何”“统计与概率”和“综合与实践”四个领域。在“数与代数”领域，《2022年课程标准》将《2011年课程标准》的“数的认识”和“数的运算”两个主题整合为“数与运算”主题，这样“数的运算”就从之前的单独主题调整为“数与运算”主题中的子主题。

加、减、乘、除四则运算是义务教育数学课程内容的重要组成部分，承担着培养学生用数学的眼光观察现实世界的育人价值，有助于培养学生的数感、运算能力和推理意识。以北师大版教材编排为例，教材对“数的运算”的编排常以自然单元呈现。例如，100以内的整数加减法就是分为6个相互衔接的单元，编排在一年级上、下两册教材中。

那么，在组织“数的运算”单元教学时，教师要如何凸显“数与运算”主题的结构化特征，从而实施“数的运算”单元整体教学呢？

一、从“数与运算”主题整合的视角分析“数的运算”

“数与运算”包括整数、分数和小数的认识及相应的加、减、乘、除四则运算。学生对整数、分数和小数的认识主要依托生活情境，并由此理解数的意义。数的运算需要以数的意义、运算的意义和运算律为基础。

1.结构化视角“研究对象+”的内涵与价值

将“数的认识”与“数的运算”整合为一个主题，可以凸显两者的紧密性。数的运算是在数的认识基础上的结构化表达，形式上是基于抽象的结构，可以表述为“研究对象+”。其中，“研究对象”可理解为数的概念，也就是整数、分数和小数。基于研究对象的“+”则指的是整数、分数、小数各自的意义、性质、四则运算方法和混合运算方法，以及它们之间的联系。史宁中教授认为，这样的主题调整可使相同学科本质的内容更具结构化，凸显学科核心内容的稳定性，强化内容的整体性和结构性，体现学科内容本质。

2.数的概念与运算的一致性

《2022年课程标准》指出：“初步体会数是对数量的抽象，感悟数的概念本质上的一致性，形成数感和符号意识；感悟数的运算以及运算之间的关系，体会数的运算本质上的一致性，形成运算能力和推理意识。”数的运算的重点在于理解算理、掌握算法，算法是对算理的抽象概括，对算理的理解最终都要追溯到数的意义和运算的意义上。

二、“数的运算”单元整体教学的原则

1.概念本质和算法的一致性

“数的运算”自然单元教材的编排是基于相同研究对象结构化的呈现，隐含数的概念的一致性：同一单元课时均聚焦于相同的研究对象，前后课时关于运算的方法也存在一致性。

例如，一年级下册“加与减（三）”单元中，学生主要学习两位数的进位加法和退位减法，解决“两位数加一位数的进位加法（28+4）”“两位数加两位数的进位加法（38+17）”“两位数减一位数的退位减法（30-7）”和“两位数减两位数的退位减法（40-28）”四个问题。学生在探索解决第一个问题“28+4”的过程中，逐步明白其算理是将相同数位上的计数单位相加，即两位数“28”十位上的数字“2”不变，只需将个位上的数字“8”和“4”相加得12，满十进一，结果为32。教师强调“相同的计数单位相加”和“满十进一”的意义，有助于学生进一步探索解决“38+17”“30-7”和“40-28”三个问题。

2.基本活动经验的一致性

数学活动经验是学生在探索与学习活动中所形成的感性意识和个性化感受。学习活动经验有助于学生探索算理并提炼算法，是学生个性化理解算理、掌握算法的基础。教师在设计“数的运算”单元整体教学时，要充分考虑单元内活动经验的可迁移性和一致性。

例如，三年级下册“除法”单元中，学生要学习并掌握两位数、三位数除以一位数的计算方法，依次解决“两位数除以一位数”“三位数除以一位数、商是三位数（包括被除数中没有0和有0的情况）”“三位数除以一位数、商是两位数”和“除法的验算”等问题。分析本单元的知识结构，笔者发现在第一课时“两位数除以一位数”的探索活动中，教材借助实物图、小棒、除法竖式等多样化表征“平均分物”的过程，使学生积累了用不同抽象水平的方式解决平均分问题的经验，掌握了两位数除以一位数的算法，也为继续学习其他平均分问题和包含除问题奠定了经验基础。通过迁移、类比两位数除以一位数的直观操作经验或者抽象的算式表达方式来解决更复杂的平均分问题和包含除问题，凸显了学生对该单元认知经验的一致性，有助于学生构建结构化的单元知识体系。

3.数学思维方式及其抽象水平的一致性

数学在培养人的思维方面有着不可替代的作用，在不同领域和主题中都有相应的思维方式，不同的思维方式之间呈现不同层级的抽象水平。通常，同样的思维方式会在同一个“数的运算”单元中反复出现，体现了数学思维方式的一致性。

例如，四年级下册“小数的意义和加减法”单元中，学生先学习小数的意义，再探索小数加减法运算（1.25+2.41）。教师要怎样引导学生理解算理、概括算法，感悟“小数加减法计算中小数点要对齐”的道理呢？在经历借助“元、角、分模型”等实物表示小数—脱离实物借助面积模型理解小数—用小数的计数单位理解小数的意义三个过程后，学生可能出现三种抽象水平的思维方式：一是仍然借助“元、角、分模型”，将相同面值的人民币摆放在一起，得到计算结果；二是借助面积模型“百格图”表示小数1.25和2.41，直观表征小数的意义，进而得出计算结果；三是根据小数的概念，通过相同计数单位相加来尝试两位小数的加减法竖式计算。本单元在解决两位小数进位加法和退位减法计算问题时，将继续迁移使用相同抽象水平的思维方式。

三、基于结构化的“数的运算”单元整体教学实施步骤

指向学科核心素养的单元整体教学设计应按单元整体教学模型指导教学。邵朝友教授和崔允漷教授认为，实施大观念统领下的单元整体教学包括“确定核心素养”“确定大观念等既有目标”“形成一致性目标体系”“设计单元评价方法”和“围绕主要问题创设学习活动”五个关键行动。马云鹏教授深刻分析了基于主题的大单元整体教学，认为基于主题的大单元整体教学有“提炼核心概念，形成系列单元”“整体分析单元学习内容和学生学习，确定学习目标”和“针对关键内容，设计体现知识与方法迁移的单元整体教学活动”三个关键要素，这里的核心概念也就是数学大概念。张丹教授和于国文教研员则提炼出了具体的实施流程（如图1），他们认为在数学大概念统领下实施促进理解与迁移的单元整体教学需依照教学模型。

分析发现，许多专家均将单元教学方案设计聚焦在“确定学科核心素养”“确定大概念”“明确单元学习目标”“形成单元关键问题”“设计系列单元学习任务”和“设计匹配的单元体系”等重要元素上。

1.从结构化主题提炼大概念

提炼核心大概念是实施单元整体教学的关键。如何提炼大概念是一直以来困扰教师的现实问题，究其原因是国内外关于大概念的本质与内涵的理解未达成一致，具体可以从“学科本质”“专家思维”“生活价值”“高通路的迁移”等不同方面进行阐述。

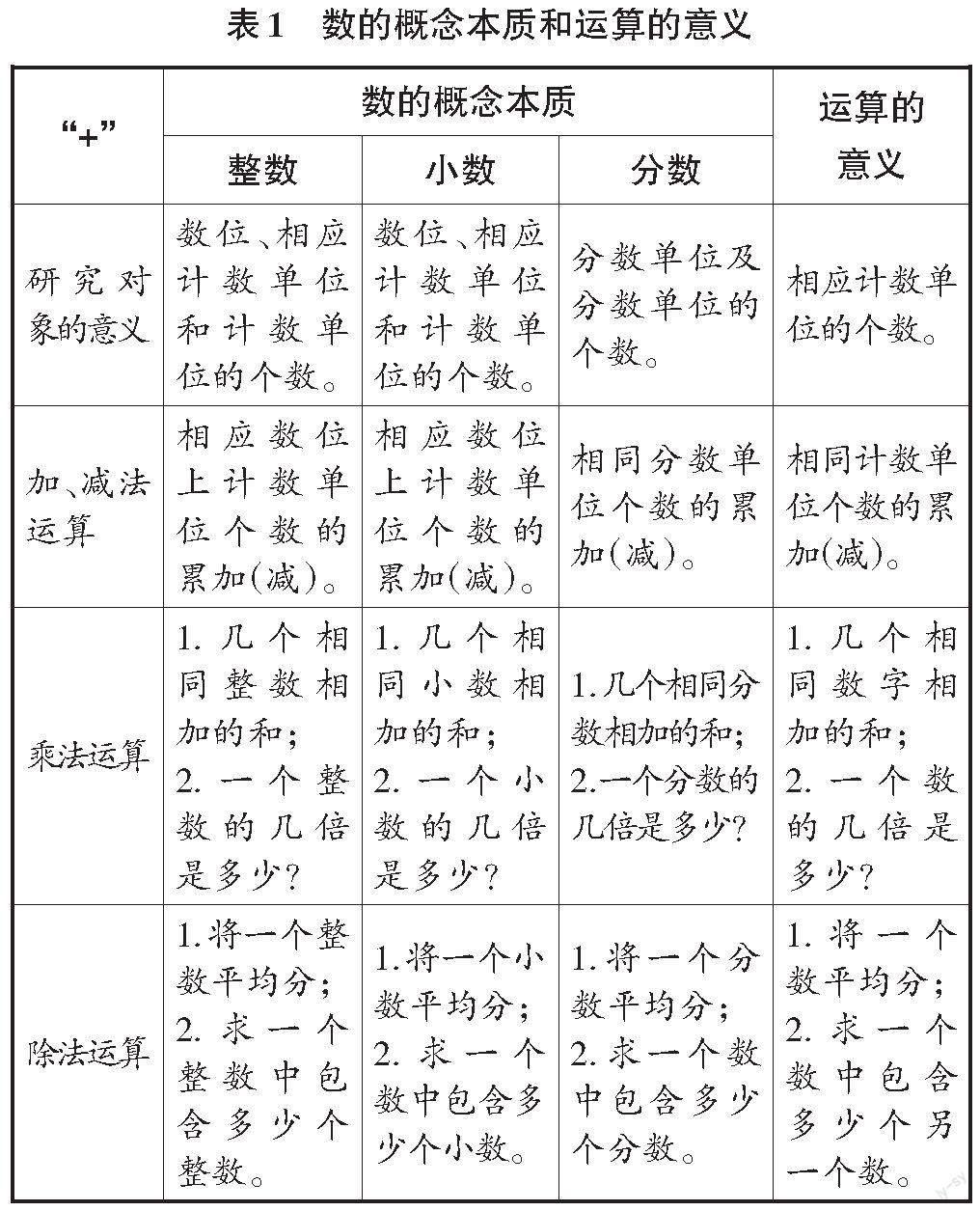
为便于小学数学教师提炼大概念，实施单元整体教学，马云鹏教授建议在聚焦数学学科结构化主题内容的前提下提炼数学大概念，这是一种更容易实践的策略。“数的运算”是“数与运算”的重要组成内容，是基于研究对象“数的概念”的“+”。提炼“数的运算”单元大概念需考虑数的概念本质和运算的意义。从数的概念的一致性上分析，计数单位是构建数的基础，由计数单位理解整数、小数和分数的构建是关键；从运算的意义的一致性上分析，减法、乘法和除法都可以由加法衍生而来。由此可以得到数的概念和运算的一致性的框架（如图2）。加、减法的一致性体现为相同计数单位的累加（减），乘法的一致性体现为计数单位（计数单位上的数字）与计数单位（计数单位上的数字）相乘，除法的一致性体现为计数单位（计数单位上的数字）与计数单位（计数单位上的数字）相除。

经过以上分析，笔者发现计数单位是“数的运算”的单元大概念，延续到“分数乘法”单元，则是“计数单位与计数单位相乘”“计数单位上的数字与计数单位上的数字相乘”这两种情况。

2.明确单元学习目标和学习评价体系

根据威金斯在《追求理解的教学设计（第二版）》的单元设计理念，以目标为导向的逆向设计是最佳的。确定单元学习目标是设计教学的前提，教师在明确单元具体目标后能更有针对性地设计单元整体教学。《2022年课程标准》将教学内容分为“内容标准”“评价标准”和“教学提示”三个部分，教师确定单元整体教学目标需要以此为基础。理解为先的教学目标包括迁移目标（T目标）、理解目标（U目标）、技能目标（K目标）。“分数乘法”单元的TUK目标和具体行为表现如表2所示。

3.确定单元关键问题

单元关键问题指向单元具体观念。通过关键问题驱动学生深度思考、开展合作与探究，是达成理解目标的关键途径。大概念统领下的单元整体教学的开展需要教师依托单元具体观念，提出驱动学生思考的关键问题。提炼单元关键问题可以根据实际情况，采取“于知识迁移中提炼核心问题”“于知识对比中提炼核心问题”和“于学科知识本质中提炼核心问题”等策略。

例如，在五年级下册“分数乘法”单元中，教师可以引导学生分别从“几个相同分数相加”和“求一个数（整数和分数两种）的几分之几”两个不同角度，探索并理解整数乘法和分数乘法的一致性。为了让学生在对比迁移中体会“求几个相同整数相加的和”与“求几个相同分数相加的和”的算法一致性，教师需要提出关键问题：“如何求几个相同分数相加的和。”同时为学生提供面积模型图、方格纸等直观学具，引导学生理解分数乘法的运算意义、算理并提炼算法。（见表3）

4.设计单元核心任务序列

学习任务是学生在关键问题和好奇心的驱动下，通过合作探究完成的具体学习活动。学习任务相比关键问题而言更加直观，它是将学生的注意力聚焦在某一个或某一系列问题的具体数学学习活动，是形成并理解单元具体观念的依托。学习任务具体指导学生需要学习什么，决定了他们怎么思考、发展和理解数学活动。

例如，在“分数乘法”单元中，教师要为学生创设问题解决和意义构建的学习任务序列（见表4），让学生在核心问题的引领下明确思考的方向，为学生提供学习的脚手架。

根据《2022年课程标准》的理念，“数的运算”是以数的概念为研究对象的“+”，其单元整体教学更加需要注重数的概念与运算的一致性，从而凸显“数与运算”主题知识的结构化。在实施单元整体教学时，教师要基于核心概念计数单位、运算的意义和数学思想提炼单元大概念，明确单元学习目标和评价体系，提出符合生活情境的关键问题及子问题，进而设计出与问题对接的学习任务序列，促使学生的学习真正发生。

［ 参 考 文 献 ］

[1] 史宁中，曹一鸣.义务教育数学课程标准（2022年版）解读[M].北京：北京师范大学出版社，2022.

[2] 中华人民共和国教育部.义务教育数学课程标准（2022年版）[S].北京：北京师范大学出版社，2022.

[3] 巩子坤，史宁中，张丹.义务教育数学课程标准修订的新视角：数的概念与运算的一致性[J].课程·教材·教法，2022，42（6）：45-51，56.

[4] 邵朝友，崔允漷.指向核心素养的教学方案设计：大观念的视角[J].全球教育展望，2017，46（6）：11-19.

[5] 马云鹏.基于结构化主题的单元整体教学：以小学数学学科为例[J].教育研究，2023，44（2）：68-78.

[6] 张丹，于国文.“观念统领”的单元教学：促进学生的理解与迁移[J].课程·教材·教法，2020，40（5）：112-118.

[7] 威金斯，麦克格泰.追求理解的教学设计（第二版）[M].闫寒冰，宋雪莲，赖平，译.上海：华东师范大学出版社，2017.

[8] 威金斯，麦格泰.理解为先模式：单元教學设计指南（一）[M].盛群力，沈祖芸，柳丰，等，译.福州：福建教育出版社，2018.

[9] 徐世凤.小学数学单元整体教学核心问题的提炼[J].教学与管理，2022（11）：56-58.

[10] 刘延革，冯林.大观念统领下单元学习任务的开发[J].中小学管理，2021（5）：32-35.