深度教研之路径的整体设计

林志辉　陈柯柯

［摘 要］路徑的整体设计在深度教研中扮演着重要的角色，它将理论学习与真实学情分析相结合，突显教师的创新性思考。文章以“圆的认识”为例，阐述深度教研下路径的整体设计。通过时间轴“目标设定—课例比较—路径思考”，将学段领域引向单元课时，再进一步引向课例的目标精准设定，并借助课例优化思考。另外，还要基于内容的整体解读和学情的整体分析，选用适切的材料和顺序。同时，以一节课走向一类课的大视野，设计出充满思考力和创新性的路径。

［关键词］深度教研；路径设计；圆的认识

［中图分类号］ G623.5［文献标识码］ A［文章编号］ 1007-9068（2023）35-0012-04

学习路径是指为了实现特定目标而设计的任务序列，涵盖学生在学习过程中需要经历的各个环节。在本文中，“路径的整体设计”是指在特级教师林志辉提出的“单元视角下的比较研究”中进行深度教研第三维度的研究。该研究基于“内容的整体解读”和“学情的整体分析”，关注静态的知识和动态的学情，借鉴大量的课例文献，深入思考、优化调试，旨在设计出最适合的学习路径。实现“路径的整体设计”需要对目标设定、课例比较和路径思考进行比较分析。

一、目标设定

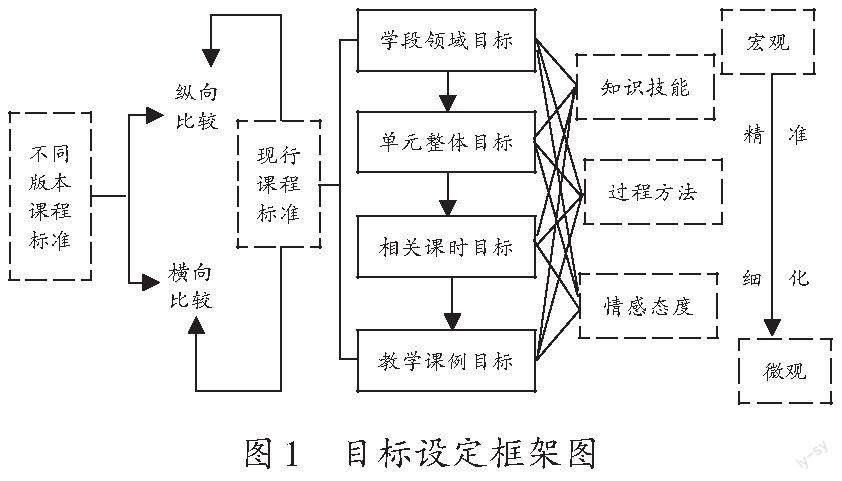
教学目标可以说是指挥棒，直接指向教学所应达成的成效。目标设定是教师对教学内容、学生知识经验和能力素养进行高度概括的过程，能充分展现教师的专业性。为了更加精确地确定教学目标，笔者采取了与常规方法不同的方式。如图1所示，要求参与研讨的教师先逐步细化学段领域目标和单元整体目标，然后解读单元内各个相关课时的目标，最后确定教学课例的目标。纵向和横向比较知识技能、过程方法和情感态度，能让教学目标从宏观走向微观，从大单元走向一节课，不断细化和精准。

1.不同版本课程标准的对比

以“圆的认识”为例，纵向比较不同时期的课程标准可发现，1986年的全日制小学数学教学大纲依然要求学生掌握圆的特征。然而，从2001年版《义务教育数学课程标准（实验稿）》开始，课程标准的要求转变为认识圆，并一直延续至今，且“认识”被定义为描述对象的特征和由来，阐述该对象与相关对象之间的区别和联系。

可以看出，随着课程标准的更迭，学生不仅需要了解圆的特征，还需要了解为什么圆会具有这样的特征。随着时间的推进，课程标准明确要求学生通过观察和操作来认识圆，注重让学生通过亲身体验来学习这部分知识。学习方式强调了学生的主动学习和动手操作。此外，课程标准对学生在技能方面的要求也更加具体：要求学生使用圆规来画圆，并注重培养学生对美的欣赏能力。

2.现行版本课程标准对比

继续以“圆的认识”为例，通过对比《义务教育数学课程标准（2022年版）》在第一学段、第三学段和第四学段不同学段领域的目标安排，聚焦第三学段六年级中圆所在单元的整体目标，梳理对比相关课时的目标，确定“圆的认识”的课例目标。

（1）学段领域目标

通过比较不同学段领域的教学目标，可以看出第一学段着重于辨认圆，关注静态、直观的整体表象。第三学段则要求学生通过观察和操作来认识圆，掌握使用圆规画圆的技能，并且了解圆周率、掌握圆周长和圆面积的计算公式，能够解决简单的与圆相关的实际问题。此外，学生还需要学会从平移、旋转和轴对称的角度来欣赏生活中的图案，并能在方格纸上设计简单的图案。在第三学段中，学生开始逐渐理解圆的特征的动态本质，为第四学段学习更抽象的圆概念打下坚实的基础。

（2）单元整体目标

基于学段领域目标，教师可以选取所在单元的“圆的周长”“圆的面积”和“扇形的认识”作为核心案例。通过横向比较教师教学用书对各节课的目标定位，确定“圆的周长”“圆的面积”以及“扇形的认识”这些课程是为了丰富学生对圆的特征的认识。由此确定本节课的目标：知识层面上为学习圆的特征打基础，技能层面上为后续进一步学习曲线图形奠定基础，培养学生的空间观念。

（3）课时、课例目标

结合学段领域目标、单元整体目标以及与相关典型案例的比较分析，从知识技能、过程方法和情感态度三个方面确定课时、课例目标为：①理解并掌握圆的特征，学会画圆；②通过探索圆的特征的过程，积累实践经验，发展空间观念；③感受数学知识之间的紧密联系，激发学习数学的兴趣。

二、课例比较

课例比较是基于充分的文献阅读，对典型案例的路径设计进行对比分析（如图2所示）。此过程主要从课例的导入、展开和练习三个方面出发，对课例的共性和个性进行抽象和聚焦，以求同寻异。通过发现课例的共性设计来确定课例的知识重难点，还要进行双向验证以确保目标设定的准确性。而对不同课例的立意点进行比较，能为路径设定提供有益的参考，同时结合学情，找到最佳的学材和教学序列，从而全面理解教学内容的广度。

1.求同寻异

以“圆的认识”为例，笔者根据课例设计的特点选取了4篇典型的课例作为比较对象，分别是佘路祥老师、肖丽丹老师和汪秀芹老师，以及冯凯老师赏析的特级教师苏明杰的课例。

从导入环节来看，这4篇课例都注重唤醒学生对圆的原有认知。他们利用生活情境或游戏等不同方式引导学生进入课题。在教学环节中，佘路祥老师和苏明杰老师利用操作和思考活动引导学生自主发现圆的相关特征，并总结出圆“一中同长”的本质属性。学生在了解圆“一中同长”的特征后，可以选择多种方法来画圆，从中感悟不同画法之间的共同属性，体会用圆规画圆的优势。汪秀芹老师和肖丽丹老师则采用先画圆再探究圆的特征的方式。这4位老师都注重探究方法的多样性，引导学生通过多次使用圆规画圆、使用不同工具画圆来认识圆的特征。其中，只有肖丽丹老师让学生研究找圆心的方法，从而让学生进一步体会圆上任意一点到圆心的距离相等。无论是先画圆后探究，还是先探究后画圆，画圆和探究圆的特征都是本节课的目标。在练习环节，这4位老师都是让学生感受生活中圆的美，强调圆的特征的应用，符合课程标准的要求。

通過比较，笔者总结出这几个课例的三个共性。（1）导入环节需要唤醒学生原有的知识或经验，关注学生的起点；（2）展开环节需要聚焦圆的特征探索，特别是圆“一中同长”的本质属性。可以引导学生在画圆的过程中探索和体会圆的特征，并通过观察、操作和表达等方式培养学生的空间观念；（3）练习环节需要拓展圆的特征的应用，并强调学生对圆的美的欣赏。

2.优化凝练

课例比较是路径设计的参考依据，但教学的主体是学生，他们的学情决定了教学的起点。只有适合学生的教学方法才能达到最好的教学效果。笔者团队提出的路径的整体设计以大量文献为基、以教学对象为主设置教学任务。为了更准确地把握学生的水平，笔者团队设计了以下三个前测问题：①在格子图中找到距离已知点学校300米的小明家（1格表示100米）；②画出你心目中的圆；③描述圆的特征。

通过对所在区域的322名学生进行调研，笔者团队发现以下情况。

第①题，找点。解决这个问题时，大多数学生都能意识到小明家可能在圆上，画出圆表示小明家可能在的位置的学生占比为70.19%，其中有19.25%的学生想到以学校为中心，在上下左右四个方向描出4个点。

第②题，画圆。令人意外的是，高达98.14%的学生能够使用圆规画圆，只有个别学生在使用圆规时稍显不熟练。大多数学生已经明确知道圆规的针尖可以用来确定圆心，圆规两脚张开的大小可以确定圆的大小。

第③题，说圆。由于学生可以通过多种渠道获取关于圆的知识，所以35.40%的学生已经能说出圆的半径、直径和圆心等概念，他们也知道圆的特征中包括“一中同长”。但通过进一步的访谈，笔者发现，学生只是停留在知道的层面，缺乏对圆的真正理解。

根据以上调研结果，以及对班级小样本的集中观察，笔者发现，学生对圆的半径、直径和圆心等概念已经有了一定的认识。面对这样的高起点，笔者尝试采用更抽象的教学方法，即通过操作和探究来引导学生从感性认识到理性认识，抽象概括出圆的本质特征，积累学习平面图形的经验，并发展空间观念。

三、路径思考

路径思考是教师在选择合适的素材、恰当的教学呈现方式和教学呈现时的思考过程，它体现了教师思想创新的深度。教师要基于目标聚焦下的高度进行概括、课例比较下的广度进行理解，依托学生的真实学习起点，选择合适的“材”，锁定适切的“序”，顺应学生的学习规律，尊重学生的真实学情。

1.“材”的选择

如“圆的认识”一课中，基于“圆的认识”前测单的数据反馈，面对学生高起点的学情，笔者摒弃了教材中用实物拓印圆和描物体边线的活动，选择课程标准中提到的格子图，让学生以不同课例中所提到的动态视角理解圆。笔者尝试设计让学生在找点的过程中理解“一中同长”的活动。导入环节选择课前让学生找距离学校300米处的小明家的素材，即选择找圆上的点的相关素材。展开环节让学生在格子图上先画一个三角形ABC，再画一个圆，使得三角形ABC的三个顶点三都在圆上，最后找出这个圆的圆心；保留线段AB，找出过线段端点A和B的圆的圆心，并辨析在同一直线上的三点为何不能在同一个圆上。练习环节不是欣赏生活中圆，而是让学生想象13个圆能组成什么图形，进而感受数学之美。

2.“序”的锁定

在“圆的认识”一课中，为了进一步加深学生的理解，笔者尝试从激活认知初识特征、探究本质丰厚特征、迁移延伸深化特征、图形想象拓展思维四个环节展开教学（如图3），带领学生找点画圆。这些环节旨在尊重学生的原有知识起点和技能经验，培养学生的空间观念。

第一个环节分两层逐步推进。第一层是通过找小明家的位置，让学生从离散点到密集点再到连续点（即圆）中初步感受到半径处处相等。第二层是通过画圆后对比圆的位置和大小，让学生认识到圆心决定了圆的位置，半径决定了圆的大小。

第二个环节分三层推进。第一层是通过以直角三角形中的某一点为圆心，让学生明白斜边和直角边长不一致时是无法画出圆的。第二层是引导学生从画一个圆到画多个圆，再到画无数个圆，让学生紧紧围绕“为什么圆心在这里？”这个问题进行思考，逐渐理解圆“一中同长”的本质特征。第三层是通过画圆，让学生感受到只有以圆心作为唯一点才能使得三角形的三个顶点都在圆上。

在第三个环节中，通过找小亮家的方式让学生体会直径的特征，并明确直径与半径的关系。

在第四个环节中，通过想象13个圆能组成什么图形来拓展学生的思维，并让他们感受到圆的美。

3.一类课的思考

单元整体视角下的路径整体设计，不仅仅是针对单个课堂的深度研讨，更重要的是用联系的眼光来看待一系列的课程。比如， “圆的认识”属于认识平面图形的一部分。在“圆的认识”之前，教材编排了四边形、长方形、正方形、平行四边形、梯形和三角形的认识内容。而“圆的认识”又是整个“圆”单元的起始课，那么它会给后续的课程如“圆的周长”“圆的面积”等带来哪些启发呢？这些问题都是路径整体设计需要研讨的内容。笔者团队倡导从一节课走向一类课，注重自然单元之间的课例设计，以及关联大单元（即同主题系列）的课例推进。

（1）圆的系列课例思考

本单元是小学阶段最后一个认识平面图形的单元，圆作为曲线图形的一部分，对学生来说是一个挑战。在整个单元中，“圆的认识”是第一课时，也是学生认识曲线图形的起始课。而本单元的系列课例需要引导学生感受动态圆的轨迹变化过程。例如，在学习圆的周长时，通过将曲线转化为直线的方式来理解圆周长的概念，可以加深对圆周率的理解。而在学习圆的面积时，通过将圆转化为长方形的方式来理解圆面积的概念，即将曲线图形转换为熟悉的直边图形能够更好地理解。在这两节课中，教师应当像在“圆的认识”一课中一样，注重学生的操作，让他们通过实际的探索来掌握圆周长和圆面积的公式，并解决一些简单的实际问题，同时也促进他们空间观念的发展。

（2）图形的认识系列课例思考

图形的认识是几何领域教学的基石，涵盖了图形测量、图形变换、图形与位置等方面的内容。它是培养学生空间意识、几何直观和推理能力的重要载体。在人教版教材中，从纵向比较的角度来看，一年级下册开始编排平面封闭图形的初步认识，着重培养学生的直观表象和整体辨析能力。到了第二学段，开始编排图形特征的初步认识，因为学生需要从整体走向元素，并逐渐从直观的认知走向分析性的思考，为第三学段学习抽象概念奠定基础。在第二学段，学生对图形的认识属于再认识的范畴，教师在概念教学中可以采用概念同化的教学路径来让学生认识图形，特别是在长方形、正方形、平行四边形、梯形和三角形的认识过程中。通过采用概念同化的教学路径，学生可以将新学习的概念与已有的相关概念进行联系和比较，从而更好地理解和掌握图形的特征。

这样的教学路径有助于学生在图形认识中深化和迁移概念，培养他们的几何思维和学科的连贯性思维。同时，路径的整体设计是培养教师创新能力的有力载体，也能够为学生的后续学习打下坚实的基础。

［ 参 考 文 献 ］

[1] 章勤琼.基于学习路径分析的小学数学教学：概述与基本框架[J].小学教学数学版，2019（Z1）：8-10.

[2] 佘路祥.主题整合：让数学学习走向深刻和多元：以《圆的认识》教学为例[J].数学教学通讯，2020（10）：21-22，37.

[3] 肖丽丹.思维可视化，让数学学习真正发生：以“圆的认识”为例谈关注学生思维发展[J].小学教学参考，2020（20）：26-27.